User:Sintel/Zeta working page

Derivation

Our goal is to derive a function that quantifies how effectively an equal division of the octave (EDO) approximates just intonation (JI). We will use the variable x to denote an EDO where x=12 represents 12edo. Importantly, we allow x to take continuous values, enabling it to represent any equal-step tuning where the step size is 1200/x cents. For example, x=8.202 corresponds to 13 equal divisions of the tritave.

To assess how well an equal temperament approximates the harmonic series, we need a function that measures the accuracy of approximation for each overtone.

The frequency ratio of the nth harmonic is n:1. In any equal temperament, to reach a ratio of n:1, we need [math]\displaystyle{ \log_2(n) }[/math] octaves, which is [math]\displaystyle{ x \log_2(n) }[/math] steps. If [math]\displaystyle{ x \log_2(n) }[/math] is very close to an integer, it means our equal temperament system can closely approximate that harmonic. If it's far from an integer, the approximation will be poor.

To quantify this proximity to integers, we can use the cosine function [math]\displaystyle{ f(x) = \cos(2 \pi x) }[/math], which peaks at integer values. This provides a simple metric where values close to 1 indicate good approximations and values close to -1 indicate poor ones.

Let's begin by considering only the first few harmonics and look at [math]\displaystyle{ f(x \log_2 2) }[/math], [math]\displaystyle{ f(x \log_2 3) }[/math], [math]\displaystyle{ f(x \log_2 4) }[/math], [math]\displaystyle{ f(x \log_2 5) }[/math].

The sum of these values gives us an overall quality measure:

[math]\displaystyle{ \sum_{n=1}^5 f(x \log_2 n) }[/math]

Plot of the cosine error function for the first 5 harmonics. Note how the peaks line up for some popular EDOs.

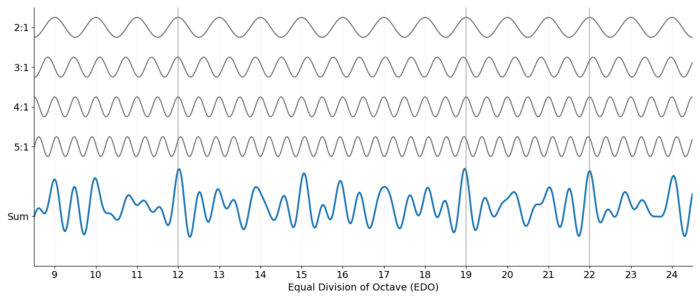
Ideally, we would like to extend this function to sum over the entire harmonic series:

[math]\displaystyle{ \sum_{n=1}^{\infty} f(x \log_2 n) }[/math]

However, this infinite sum does not converge. To address this issue, we can introduce a weighting factor that diminishes the contribution of higher harmonics:

[math]\displaystyle{ \begin{aligned} F(x) &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} f(x \log_2 n) \\ &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} \cos(2 \pi x \log_2 n) \end{aligned} }[/math]

This series converges provided that [math]\displaystyle{ \sigma \gt 1 }[/math], with the parameter sigma controlling how quickly the influence of higher harmonics declines.

We can reformulate this expression using Euler's formula [math]\displaystyle{ e^{ix} = \cos x + i \sin x }[/math], and replace the cosine with the real part of a complex exponential:

[math]\displaystyle{ \begin{aligned} F(x) &= \sum_{n=1}^{\infty} \frac{1}{n^\sigma} \mathrm{Re} \left( e^{-2 \pi i x \log_2 n} \right) \\ &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} e^{-2 \pi i x \log_2 n} \end{aligned} }[/math]

Using properties of logarithms, we know that [math]\displaystyle{ e^{x \log_2 n} = n^{\frac{x}{\ln 2}} }[/math], which gives us:

[math]\displaystyle{ \begin{aligned} F(x) &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} n^{-\frac{2 \pi}{\ln 2} i x} \\ \end{aligned} }[/math]

To clean this up a bit we will make a substitution and set [math]\displaystyle{ t = \tfrac{2 \pi}{\ln 2} x }[/math].

[math]\displaystyle{ \begin{aligned} F(x) &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^\sigma} n^{-i t} \\ &= \mathrm{Re} \, \sum_{n=1}^{\infty} \frac{1}{n^{\sigma + i t}} \end{aligned} }[/math]

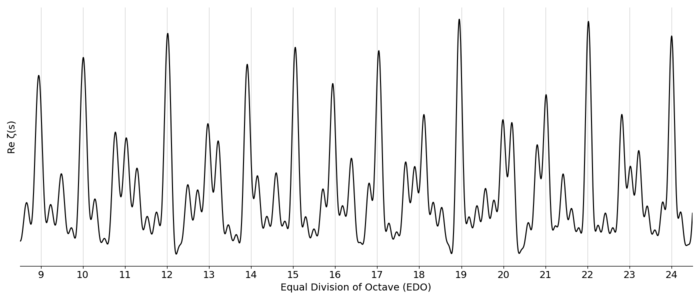
This final expression is precisely the definition of the Riemann zeta function [math]\displaystyle{ \zeta(s) }[/math] evaluated at the complex value [math]\displaystyle{ s = \sigma + i t = \sigma + \tfrac{2 \pi i}{\ln(2)} x }[/math]. Thus, our measure of tuning quality can be expressed directly in terms of this fundamental mathematical function:

[math]\displaystyle{ F(x) = \mathrm{Re} \, \zeta \left( \sigma + \frac{2 \pi i}{\ln(2)} x \right) }[/math]

Real part of zeta function for sigma = 1.