25edo: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
Wikispaces>TallKite
**Imported revision 602808482 - Original comment: **
Wikispaces>FREEZE
No edit summary
Line 1: Line 1:
<h2>IMPORTED REVISION FROM WIKISPACES</h2>
__FORCETOC__
This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
=<span style="color: #006b2e; font-family: 'Times New Roman',Times,serif; font-size: 113%;">25 tone equal temperament</span>=
: This revision was by author [[User:TallKite|TallKite]] and made on <tt>2016-12-25 18:52:38 UTC</tt>.<br>
: The original revision id was <tt>602808482</tt>.<br>
: The revision comment was: <tt></tt><br>
The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
<h4>Original Wikitext content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">[[toc|flat]]
=&lt;span style="color: #006b2e; font-family: 'Times New Roman',Times,serif; font-size: 113%;"&gt;25 tone equal temperament&lt;/span&gt;=  


25EDO divides the [[octave]] in 25 equal steps of exact size 48 [[cent]]s each. It is a good way to tune the [[Blackwood temperament]], which takes the very sharp fifths of [[5EDO]] as a given, tempers out 28/27 and 49/48, and attempts to optimize the tunings for 5 ([[5_4|5/4]]) and 7 ([[7_4|7/4]]). It also tunes sixix temperament with a sharp fifth. It supplies the optimal patent val for the 11-limit 6&amp;25 temperament tempering out 49/48, 77/75 and 605/576, and the 13-limit extension also tempering out 66/65.
25EDO divides the [[Octave|octave]] in 25 equal steps of exact size 48 [[cent|cent]]s each. It is a good way to tune the [[Blackwood_temperament|Blackwood temperament]], which takes the very sharp fifths of [[5edo|5EDO]] as a given, tempers out 28/27 and 49/48, and attempts to optimize the tunings for 5 ([[5/4|5/4]]) and 7 ([[7/4|7/4]]). It also tunes sixix temperament with a sharp fifth. It supplies the optimal patent val for the 11-limit 6&amp;25 temperament tempering out 49/48, 77/75 and 605/576, and the 13-limit extension also tempering out 66/65.


25EDO has fifths 18 cents sharp, but its major thirds are excellent and its 7/4 is acceptable. Moreover, in full 7-limit including the 3, it is not [[consistent]]. It therefore makes sense to use it as a 2.5.7 [[Just intonation subgroups|subgroup]] tuning. Looking just at 2, 5, and 7, it equates five [[8_7|8/7]]s with the octave, and so tempers out (8/7)^5 / 2 = 16807/16384. It also equates a [[128_125|128/125]] [[diesis]] and two [[septimal tritones]] of [[7_5|7/5]] with the octave, and hence tempers out 3136/3125. If we want to temper out both of these and also have decent fifths, the obvious solution is [[50EDO]]. An alternative fifth, 14\25, which is 672 cents, provides an alternative very flat fifth which can be used for [[mavila]] temperament.
25EDO has fifths 18 cents sharp, but its major thirds are excellent and its 7/4 is acceptable. Moreover, in full 7-limit including the 3, it is not [[consistent|consistent]]. It therefore makes sense to use it as a 2.5.7 [[Just_intonation_subgroups|subgroup]] tuning. Looking just at 2, 5, and 7, it equates five [[8/7|8/7]]s with the octave, and so tempers out (8/7)^5 / 2 = 16807/16384. It also equates a [[128/125|128/125]] [[diesis|diesis]] and two [[septimal_tritones|septimal tritones]] of [[7/5|7/5]] with the octave, and hence tempers out 3136/3125. If we want to temper out both of these and also have decent fifths, the obvious solution is [[50edo|50EDO]]. An alternative fifth, 14\25, which is 672 cents, provides an alternative very flat fifth which can be used for [[Mavila|mavila]] temperament.


If 5/4 and 7/4 aren't good enough, it also does 17/16 and 19/16, just like 12EDO. In fact, on the [[k*N subgroups|2*25 subgroup]] 2.9.5.7.33.39.17.19 it provides the same tuning and tempers out the same commas as 50et, which makes for a wide range of harmony.
If 5/4 and 7/4 aren't good enough, it also does 17/16 and 19/16, just like 12EDO. In fact, on the [[k*N_subgroups|2*25 subgroup]] 2.9.5.7.33.39.17.19 it provides the same tuning and tempers out the same commas as 50et, which makes for a wide range of harmony.


=Music=  
=Music=
//[[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Rapoport/StudyInFives.mp3|Study in Fives]]// by [[http://en.wikipedia.org/wiki/Paul_Rapoport_%28music_critic%29|Paul Rapoport]]
''[http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Rapoport/StudyInFives.mp3 Study in Fives]'' by [http://en.wikipedia.org/wiki/Paul_Rapoport_%28music_critic%29 Paul Rapoport]
[[http://chrisvaisvil.com/?p=2377|Fantasy for Piano in 25 Note per Octave Tuning]] //[[http://micro.soonlabel.com/25edo/fantasy_for_piano_in_25_edo.mp3|play]]// by Chris Vaisvil
//[[http://micro.soonlabel.com/gene_ward_smith/Others/Fiale/flat%20fourth%20blues.mp3|Flat fourth blues]]// by Fabrizio Fulvio Fausto Fiale


[[media type="file" key="25edochorale.mid" width="300" height="50"]] [[file:25edochorale.mid]] Peter Kosmorsky (10/14/10, 2.5.7 subgroup, a friend responded "The &lt;span class="il"&gt;25edo&lt;/span&gt; canon has a nice theme, but all the harmonizations from there are laughably dissonant. I showed them to my roomie and he found it disturbing, hahaha. He had an unintentional physical reaction to it with his mouth in which his muscles did a smirk sort of thing, without him even trying to, hahaha. So, my point; this I think this 25 edo idea was an example of where tonal thinking doesn't suit the sound of the scale.")
[http://chrisvaisvil.com/?p=2377 Fantasy for Piano in 25 Note per Octave Tuning] ''[http://micro.soonlabel.com/25edo/fantasy_for_piano_in_25_edo.mp3 play]'' by Chris Vaisvil
[[media type="file" key="25 edo prelude largo.mid" width="300" height="50"]] [[file:25 edo prelude largo.mid]] Peter Kosmorsky (2011, Blackwood)


=Intervals=
''[http://micro.soonlabel.com/gene_ward_smith/Others/Fiale/flat%20fourth%20blues.mp3 Flat fourth blues]'' by Fabrizio Fulvio Fausto Fiale


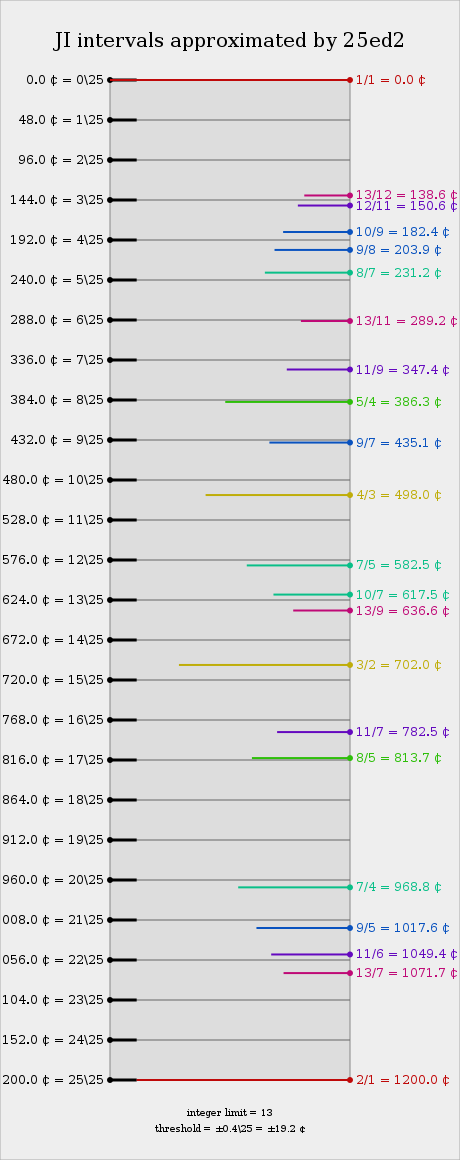
||= Degrees ||= Cents ||= Approximate
[[File:25edochorale.mid]] [[:File:25edochorale.mid|25edochorale.mid]] Peter Kosmorsky (10/14/10, 2.5.7 subgroup, a friend responded "The <span style="">25edo</span> canon has a nice theme, but all the harmonizations from there are laughably dissonant. I showed them to my roomie and he found it disturbing, hahaha. He had an unintentional physical reaction to it with his mouth in which his muscles did a smirk sort of thing, without him even trying to, hahaha. So, my point; this I think this 25 edo idea was an example of where tonal thinking doesn't suit the sound of the scale.")
Ratios* ||= Armodue
 
Notation ||||||= [[xenharmonic/Ups and Downs Notation|ups and downs notation]] ||
[[File:25_edo_prelude_largo.mid]] [[:File:25_edo_prelude_largo.mid|25 edo prelude largo.mid]] Peter Kosmorsky (2011, Blackwood)
||= 0 ||= 0 ||= 1/1 ||= 1 ||= P1 ||= perfect 1sn ||= D, Eb ||
||= 1 ||= 48 ||= 33/32, 39/38, 34/33 ||= 1# ||= ^1, ^m2 ||= up 1sn, upminor 2nd ||= D^, Eb^ ||
||= 2 ||= 96 ||= 17/16, 20/19, 18/17 ||= 2b ||= ^^m2 ||= double-upminor 2nd ||= Eb^^ ||
||= 3 ||= 144 ||= 12/11, 38/35 ||= 2 ||= vvM2 ||= double-downmajor 2nd ||= Evv ||
||= 4 ||= 192 ||= 9/8, 10/9, 19/17 ||= 2# ||= vM2 ||= downmajor 2nd ||= Ev ||
||= 5· ||= 240 ||= 8/7 ||= 3b ||= M2, m3 ||= major 2nd, minor 3rd ||= E, F ||
||= 6 ||= 288 ||= 19/16, 20/17 ||= 3 ||= ^m3 ||= upminor 3rd ||= F^ ||
||= 7 ||= 336 ||= 39/32, 17/14, 40/33 ||= 3# ||= ^^m3 ||= double-upminor 3rd ||= F^^ ||
||= 8· ||= 384 ||= 5/4 ||= 4b ||= vvM3 ||= double-downmajor 3rd ||= F#vv ||
||= 9 ||= 432 ||= 9/7, 32/25, 50/39 ||= 4 ||= vM3 ||= downmajor ||= F#v ||
||= 10 ||= 480 ||= 33/25, 25/19 ||= 4#/5b ||= M3, P4 ||= major 3rd, perfect 4th ||= F#, G ||
||= 11· ||= 528 ||= 31/21, 34/25 ||= 5 ||= ^4 ||= up 4th ||= G^ ||
||= 12 ||= 576 ||= 7/5, 39/28 ||= 5# ||= ^^4,^^d5 ||= double-up 4th,
double-up dim 5th ||= G^^, Ab^^ ||
||= 13 ||= 624 ||= 10/7, 56/39 ||= 6b ||= vvA4,vv5 ||= double-down aug 4th,
double-down 5th ||= G#vv, Avv ||
||= 14· ||= 672 ||= 42/31, 25/17 ||= 6 ||= v5 ||= down 5th ||= Av ||
||= 15 ||= 720 ||= 50/33, 38/25 ||= 6# ||= P5, m6 ||= perfect 5th, minor 6th ||= A, Bb ||
||= 16 ||= 768 ||= 14/9, 25/16, 39/25 ||= 7b ||= ^m6 ||= upminor 6th ||= Bb^ ||
||= 17· ||= 816 ||= 8/5 ||= 7 ||= ^^m6 ||= double-upminor 6th ||= Bb^^ ||
||= 18 ||= 864 ||= 64/39, 28/17, 33/20 ||= 7# ||= vvM6 ||= double-downmajor 6th ||= Bvv ||
||= 19 ||= 912 ||= 32/19, 17/10 ||= 8b ||= vM6 ||= downmajor 6th ||= Bv ||
||= 20· ||= 960 ||= 7/4 ||= 8 ||= M6, m7 ||= major 6th, minor 7th ||= B, C ||
||= 21 ||= 1008 ||= 16/9, 9/5, 34/19 ||= 8# ||= ^m7 ||= upminor 7th ||= C^ ||
||= 22 ||= 1056 ||= 11/6, 35/19 ||= 9b ||= ^^m7 ||= double-upminor 7th ||= C^^ ||
||= 23 ||= 1104 ||= 32/17, 17/9, 19/10 ||= 9 ||= vvM7 ||= double-downmajor 7th ||= C#vv ||
||= 24 ||= 1152 ||= 33/17, 64/33, 76/39 ||= 9#/1b ||= vM7 ||= downmajor 7th ||= C#v ||
||= 25 ||= 1200 ||= 2/1 ||= 1 ||= P8 ||= perfect 8ve ||= C#, D ||
*based on treating 25-EDO as a 2.9.5.7.33.39.17.19 subgroup; other approaches are possible.


[[media type="custom" key="25100128"]]
=Intervals=


[[file:25ed2-001.svg]]
{| class="wikitable"
|-
| style="text-align:center;" | Degrees
| style="text-align:center;" | Cents
| style="text-align:center;" | Approximate


Ratios*
| style="text-align:center;" | Armodue


=Relationship to Armodue=  
Notation
| colspan="3" style="text-align:center;" | [[Ups_and_Downs_Notation|ups and downs notation]]
|-
| style="text-align:center;" | 0
| style="text-align:center;" | 0
| style="text-align:center;" | 1/1
| style="text-align:center;" | 1
| style="text-align:center;" | P1
| style="text-align:center;" | perfect 1sn
| style="text-align:center;" | D, Eb
|-
| style="text-align:center;" | 1
| style="text-align:center;" | 48
| style="text-align:center;" | 33/32, 39/38, 34/33
| style="text-align:center;" | 1#
| style="text-align:center;" | ^1, ^m2
| style="text-align:center;" | up 1sn, upminor 2nd
| style="text-align:center;" | D^, Eb^
|-
| style="text-align:center;" | 2
| style="text-align:center;" | 96
| style="text-align:center;" | 17/16, 20/19, 18/17
| style="text-align:center;" | 2b
| style="text-align:center;" | ^^m2
| style="text-align:center;" | double-upminor 2nd
| style="text-align:center;" | Eb^^
|-
| style="text-align:center;" | 3
| style="text-align:center;" | 144
| style="text-align:center;" | 12/11, 38/35
| style="text-align:center;" | 2
| style="text-align:center;" | vvM2
| style="text-align:center;" | double-downmajor 2nd
| style="text-align:center;" | Evv
|-
| style="text-align:center;" | 4
| style="text-align:center;" | 192
| style="text-align:center;" | 9/8, 10/9, 19/17
| style="text-align:center;" | 2#
| style="text-align:center;" | vM2
| style="text-align:center;" | downmajor 2nd
| style="text-align:center;" | Ev
|-
| style="text-align:center;" | 5·
| style="text-align:center;" | 240
| style="text-align:center;" | 8/7
| style="text-align:center;" | 3b
| style="text-align:center;" | M2, m3
| style="text-align:center;" | major 2nd, minor 3rd
| style="text-align:center;" | E, F
|-
| style="text-align:center;" | 6
| style="text-align:center;" | 288
| style="text-align:center;" | 19/16, 20/17
| style="text-align:center;" | 3
| style="text-align:center;" | ^m3
| style="text-align:center;" | upminor 3rd
| style="text-align:center;" | F^
|-
| style="text-align:center;" | 7
| style="text-align:center;" | 336
| style="text-align:center;" | 39/32, 17/14, 40/33
| style="text-align:center;" | 3#
| style="text-align:center;" | ^^m3
| style="text-align:center;" | double-upminor 3rd
| style="text-align:center;" | F^^
|-
| style="text-align:center;" | 8·
| style="text-align:center;" | 384
| style="text-align:center;" | 5/4
| style="text-align:center;" | 4b
| style="text-align:center;" | vvM3
| style="text-align:center;" | double-downmajor 3rd
| style="text-align:center;" | F#vv
|-
| style="text-align:center;" | 9
| style="text-align:center;" | 432
| style="text-align:center;" | 9/7, 32/25, 50/39
| style="text-align:center;" | 4
| style="text-align:center;" | vM3
| style="text-align:center;" | downmajor
| style="text-align:center;" | F#v
|-
| style="text-align:center;" | 10
| style="text-align:center;" | 480
| style="text-align:center;" | 33/25, 25/19
| style="text-align:center;" | 4#/5b
| style="text-align:center;" | M3, P4
| style="text-align:center;" | major 3rd, perfect 4th
| style="text-align:center;" | F#, G
|-
| style="text-align:center;" | 11·
| style="text-align:center;" | 528
| style="text-align:center;" | 31/21, 34/25
| style="text-align:center;" | 5
| style="text-align:center;" | ^4
| style="text-align:center;" | up 4th
| style="text-align:center;" | G^
|-
| style="text-align:center;" | 12
| style="text-align:center;" | 576
| style="text-align:center;" | 7/5, 39/28
| style="text-align:center;" | 5#
| style="text-align:center;" | ^^4,^^d5
| style="text-align:center;" | double-up 4th,


Like [[16edo|16-EDO]] and [[23edo|23-EDO]], 25-EDO contains the 9-note "Superdiatonic" scale of [[7L 2s|7L2s]] (LLLsLLLLs) that is generated by a circle of heavily-flattened 3/2s (ranging in size from 5\9-EDO or 666.67 cents, to 4\7-EDO or 685.71 cents). The 25-EDO generator for this scale is the 672-cent interval. This allows 25-EDO to be used with the [[Armodue theory|Armodue]] notation system in much the same way that [[19edo|19-EDO]] is used with the standard diatonic notation; see the above interval chart for the Armodue names. Because the 25-EDO Armodue 6th is flatter than that of 16-EDO (the middle of the Armodue spectrum), sharps are lower in pitch than enharmonic flats.
double-up dim 5th
| style="text-align:center;" | G^^, Ab^^
|-
| style="text-align:center;" | 13
| style="text-align:center;" | 624
| style="text-align:center;" | 10/7, 56/39
| style="text-align:center;" | 6b
| style="text-align:center;" | vvA4,vv5
| style="text-align:center;" | double-down aug 4th,


=Commas=
double-down 5th
25 EDO tempers out the following commas. (Note: This assumes the val &lt; 25 40 58 70 86 93 |.)
| style="text-align:center;" | G#vv, Avv
||~ Comma ||~ Monzo ||~ Value (Cents) ||~ Name 1 ||~ Name 2 ||~ Name 3 ||
|-
||= 256/243 ||&lt; | 8 -5 &gt; ||&gt; 90.22 ||= Limma ||= Pythagorean Minor 2nd ||=   ||
| style="text-align:center;" | 14·
||= 3125/3072 ||&lt; | -10 -1 5 &gt; ||&gt; 29.61 ||= Small Diesis ||= Magic Comma ||=   ||
| style="text-align:center;" | 672
||=   ||&lt; | 38 -2 -15 &gt; ||&gt; 1.38 ||= Hemithirds Comma ||=   ||=   ||
| style="text-align:center;" | 42/31, 25/17
||= 16807/16384 || | -14 0 0 5 &gt; ||&gt; 44.13 ||  ||  ||  ||
| style="text-align:center;" | 6
||= 49/48 ||&lt; | -4 -1 0 2 &gt; ||&gt; 35.70 ||= Slendro Diesis ||=   ||=   ||
| style="text-align:center;" | v5
||= 64/63 ||&lt; | 6 -2 0 -1 &gt; ||&gt; 27.26 ||= Septimal Comma ||= Archytas' Comma ||= Leipziger Komma ||
| style="text-align:center;" | down 5th
||= 3125/3087 ||&lt; | 0 -2 5 -3 &gt; ||&gt; 21.18 ||= Gariboh ||=   ||=   ||
| style="text-align:center;" | Av
||= 50421/50000 ||&lt; | -4 1 -5 5 &gt; ||&gt; 14.52 ||= Trimyna ||=   ||=   ||
|-
||= 1029/1024 ||&lt; | -10 1 0 3 &gt; ||&gt; 8.43 ||= Gamelisma ||=   ||=   ||
| style="text-align:center;" | 15
||= 3136/3125 ||&lt; | 6 0 -5 2 &gt; ||&gt; 6.08 ||= Hemimean ||=   ||=   ||
| style="text-align:center;" | 720
||= 65625/65536 ||&lt; | -16 1 5 1 &gt; ||&gt; 2.35 ||= Horwell ||=   ||=   ||
| style="text-align:center;" | 50/33, 38/25
||= 100/99 ||&lt; | 2 -2 2 0 -1 &gt; ||&gt; 17.40 ||= Ptolemisma ||=   ||=   ||
| style="text-align:center;" | 6#
||= 176/175 ||&lt; | 4 0 -2 -1 1 &gt; ||&gt; 9.86 ||= Valinorsma ||=   ||=   ||
| style="text-align:center;" | P5, m6
||= 91/90 ||&lt; | -1 -2 -1 1 0 1 &gt; ||&gt; 19.13 ||= Superleap ||=   ||=   ||
| style="text-align:center;" | perfect 5th, minor 6th
||= 676/675 ||&lt; | 2 -3 -2 0 0 2 &gt; ||&gt; 2.56 ||= Parizeksma ||=   ||=   ||
| style="text-align:center;" | A, Bb
|-
| style="text-align:center;" | 16
| style="text-align:center;" | 768
| style="text-align:center;" | 14/9, 25/16, 39/25
| style="text-align:center;" | 7b
| style="text-align:center;" | ^m6
| style="text-align:center;" | upminor 6th
| style="text-align:center;" | Bb^
|-
| style="text-align:center;" | 17·
| style="text-align:center;" | 816
| style="text-align:center;" | 8/5
| style="text-align:center;" | 7
| style="text-align:center;" | ^^m6
| style="text-align:center;" | double-upminor 6th
| style="text-align:center;" | Bb^^
|-
| style="text-align:center;" | 18
| style="text-align:center;" | 864
| style="text-align:center;" | 64/39, 28/17, 33/20
| style="text-align:center;" | 7#
| style="text-align:center;" | vvM6
| style="text-align:center;" | double-downmajor 6th
| style="text-align:center;" | Bvv
|-
| style="text-align:center;" | 19
| style="text-align:center;" | 912
| style="text-align:center;" | 32/19, 17/10
| style="text-align:center;" | 8b
| style="text-align:center;" | vM6
| style="text-align:center;" | downmajor 6th
| style="text-align:center;" | Bv
|-
| style="text-align:center;" | 20·
| style="text-align:center;" | 960
| style="text-align:center;" | 7/4
| style="text-align:center;" | 8
| style="text-align:center;" | M6, m7
| style="text-align:center;" | major 6th, minor 7th
| style="text-align:center;" | B, C
|-
| style="text-align:center;" | 21
| style="text-align:center;" | 1008
| style="text-align:center;" | 16/9, 9/5, 34/19
| style="text-align:center;" | 8#
| style="text-align:center;" | ^m7
| style="text-align:center;" | upminor 7th
| style="text-align:center;" | C^
|-
| style="text-align:center;" | 22
| style="text-align:center;" | 1056
| style="text-align:center;" | 11/6, 35/19
| style="text-align:center;" | 9b
| style="text-align:center;" | ^^m7
| style="text-align:center;" | double-upminor 7th
| style="text-align:center;" | C^^
|-
| style="text-align:center;" | 23
| style="text-align:center;" | 1104
| style="text-align:center;" | 32/17, 17/9, 19/10
| style="text-align:center;" | 9
| style="text-align:center;" | vvM7
| style="text-align:center;" | double-downmajor 7th
| style="text-align:center;" | C#vv
|-
| style="text-align:center;" | 24
| style="text-align:center;" | 1152
| style="text-align:center;" | 33/17, 64/33, 76/39
| style="text-align:center;" | 9#/1b
| style="text-align:center;" | vM7
| style="text-align:center;" | downmajor 7th
| style="text-align:center;" | C#v
|-
| style="text-align:center;" | 25
| style="text-align:center;" | 1200
| style="text-align:center;" | 2/1
| style="text-align:center;" | 1
| style="text-align:center;" | P8
| style="text-align:center;" | perfect 8ve
| style="text-align:center;" | C#, D
|}
*based on treating 25-EDO as a 2.9.5.7.33.39.17.19 subgroup; other approaches are possible.


=A 25edo keyboard=
[[File:25ed2-001.svg|alt=alt : Your browser has no SVG support.]]


[[image:mm25.PNG]]</pre></div>
[[:File:25ed2-001.svg|25ed2-001.svg]]
<h4>Original HTML content:</h4>
<div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html">&lt;html&gt;&lt;head&gt;&lt;title&gt;25edo&lt;/title&gt;&lt;/head&gt;&lt;body&gt;&lt;!-- ws:start:WikiTextTocRule:15:&amp;lt;img id=&amp;quot;wikitext@@toc@@flat&amp;quot; class=&amp;quot;WikiMedia WikiMediaTocFlat&amp;quot; title=&amp;quot;Table of Contents&amp;quot; src=&amp;quot;/site/embedthumbnail/toc/flat?w=100&amp;amp;h=16&amp;quot;/&amp;gt; --&gt;&lt;!-- ws:end:WikiTextTocRule:15 --&gt;&lt;!-- ws:start:WikiTextTocRule:16: --&gt;&lt;a href="#x25 tone equal temperament"&gt;25 tone equal temperament&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:16 --&gt;&lt;!-- ws:start:WikiTextTocRule:17: --&gt; | &lt;a href="#Music"&gt;Music&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:17 --&gt;&lt;!-- ws:start:WikiTextTocRule:18: --&gt; | &lt;a href="#Intervals"&gt;Intervals&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:18 --&gt;&lt;!-- ws:start:WikiTextTocRule:19: --&gt; | &lt;a href="#Relationship to Armodue"&gt;Relationship to Armodue&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:19 --&gt;&lt;!-- ws:start:WikiTextTocRule:20: --&gt; | &lt;a href="#Commas"&gt;Commas&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:20 --&gt;&lt;!-- ws:start:WikiTextTocRule:21: --&gt; | &lt;a href="#A 25edo keyboard"&gt;A 25edo keyboard&lt;/a&gt;&lt;!-- ws:end:WikiTextTocRule:21 --&gt;&lt;!-- ws:start:WikiTextTocRule:22: --&gt;
&lt;!-- ws:end:WikiTextTocRule:22 --&gt;&lt;!-- ws:start:WikiTextHeadingRule:3:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc0"&gt;&lt;a name="x25 tone equal temperament"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:3 --&gt;&lt;span style="color: #006b2e; font-family: 'Times New Roman',Times,serif; font-size: 113%;"&gt;25 tone equal temperament&lt;/span&gt;&lt;/h1&gt;
&lt;br /&gt;
25EDO divides the &lt;a class="wiki_link" href="/octave"&gt;octave&lt;/a&gt; in 25 equal steps of exact size 48 &lt;a class="wiki_link" href="/cent"&gt;cent&lt;/a&gt;s each. It is a good way to tune the &lt;a class="wiki_link" href="/Blackwood%20temperament"&gt;Blackwood temperament&lt;/a&gt;, which takes the very sharp fifths of &lt;a class="wiki_link" href="/5EDO"&gt;5EDO&lt;/a&gt; as a given, tempers out 28/27 and 49/48, and attempts to optimize the tunings for 5 (&lt;a class="wiki_link" href="/5_4"&gt;5/4&lt;/a&gt;) and 7 (&lt;a class="wiki_link" href="/7_4"&gt;7/4&lt;/a&gt;). It also tunes sixix temperament with a sharp fifth. It supplies the optimal patent val for the 11-limit 6&amp;amp;25 temperament tempering out 49/48, 77/75 and 605/576, and the 13-limit extension also tempering out 66/65.&lt;br /&gt;
&lt;br /&gt;
25EDO has fifths 18 cents sharp, but its major thirds are excellent and its 7/4 is acceptable. Moreover, in full 7-limit including the 3, it is not &lt;a class="wiki_link" href="/consistent"&gt;consistent&lt;/a&gt;. It therefore makes sense to use it as a 2.5.7 &lt;a class="wiki_link" href="/Just%20intonation%20subgroups"&gt;subgroup&lt;/a&gt; tuning. Looking just at 2, 5, and 7, it equates five &lt;a class="wiki_link" href="/8_7"&gt;8/7&lt;/a&gt;s with the octave, and so tempers out (8/7)^5 / 2 = 16807/16384. It also equates a &lt;a class="wiki_link" href="/128_125"&gt;128/125&lt;/a&gt; &lt;a class="wiki_link" href="/diesis"&gt;diesis&lt;/a&gt; and two &lt;a class="wiki_link" href="/septimal%20tritones"&gt;septimal tritones&lt;/a&gt; of &lt;a class="wiki_link" href="/7_5"&gt;7/5&lt;/a&gt; with the octave, and hence tempers out 3136/3125. If we want to temper out both of these and also have decent fifths, the obvious solution is &lt;a class="wiki_link" href="/50EDO"&gt;50EDO&lt;/a&gt;. An alternative fifth, 14\25, which is 672 cents, provides an alternative very flat fifth which can be used for &lt;a class="wiki_link" href="/mavila"&gt;mavila&lt;/a&gt; temperament.&lt;br /&gt;
&lt;br /&gt;
If 5/4 and 7/4 aren't good enough, it also does 17/16 and 19/16, just like 12EDO. In fact, on the &lt;a class="wiki_link" href="/k%2AN%20subgroups"&gt;2*25 subgroup&lt;/a&gt; 2.9.5.7.33.39.17.19 it provides the same tuning and tempers out the same commas as 50et, which makes for a wide range of harmony.&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:5:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc1"&gt;&lt;a name="Music"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:5 --&gt;Music&lt;/h1&gt;
&lt;em&gt;&lt;a class="wiki_link_ext" href="http://clones.soonlabel.com/public/micro/gene_ward_smith/Others/Rapoport/StudyInFives.mp3" rel="nofollow"&gt;Study in Fives&lt;/a&gt;&lt;/em&gt; by &lt;a class="wiki_link_ext" href="http://en.wikipedia.org/wiki/Paul_Rapoport_%28music_critic%29" rel="nofollow"&gt;Paul Rapoport&lt;/a&gt;&lt;br /&gt;
&lt;a class="wiki_link_ext" href="http://chrisvaisvil.com/?p=2377" rel="nofollow"&gt;Fantasy for Piano in 25 Note per Octave Tuning&lt;/a&gt; &lt;em&gt;&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/25edo/fantasy_for_piano_in_25_edo.mp3" rel="nofollow"&gt;play&lt;/a&gt;&lt;/em&gt; by Chris Vaisvil&lt;br /&gt;
&lt;em&gt;&lt;a class="wiki_link_ext" href="http://micro.soonlabel.com/gene_ward_smith/Others/Fiale/flat%20fourth%20blues.mp3" rel="nofollow"&gt;Flat fourth blues&lt;/a&gt;&lt;/em&gt; by Fabrizio Fulvio Fausto Fiale&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextMediaRule:0:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/file-audio/25edochorale.mid?h=50&amp;amp;w=300&amp;quot; class=&amp;quot;WikiMedia WikiMediaFile&amp;quot; id=&amp;quot;wikitext@@media@@type=&amp;amp;quot;file&amp;amp;quot; key=&amp;amp;quot;25edochorale.mid&amp;amp;quot; width=&amp;amp;quot;300&amp;amp;quot; height=&amp;amp;quot;50&amp;amp;quot;&amp;quot; title=&amp;quot;Local Media File&amp;quot;height=&amp;quot;50&amp;quot; width=&amp;quot;300&amp;quot;/&amp;gt; --&gt;&lt;embed type="audio/midi" style="cursor:hand; cursor:pointer;" src="http://xenharmonic.wikispaces.com/file/view/25edochorale.mid" width="300" height="50" autoplay="false" target="myself" controller="true" loop="false" scale="aspect" bgcolor="#FFFFFF" pluginspage="http://www.apple.com/quicktime/download/"&gt;&lt;/embed&gt;&lt;!-- ws:end:WikiTextMediaRule:0 --&gt; &lt;!-- ws:start:WikiTextFileRule:680:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/file/25edochorale.mid?h=52&amp;amp;w=320&amp;quot; class=&amp;quot;WikiFile&amp;quot; id=&amp;quot;wikitext@@file@@25edochorale.mid&amp;quot; title=&amp;quot;File: 25edochorale.mid&amp;quot; width=&amp;quot;320&amp;quot; height=&amp;quot;52&amp;quot; /&amp;gt; --&gt;&lt;div class="objectEmbed"&gt;&lt;a href="/file/view/25edochorale.mid/314425794/25edochorale.mid" onclick="ws.common.trackFileLink('/file/view/25edochorale.mid/314425794/25edochorale.mid');"&gt;&lt;img src="http://c1.wikicdn.com/i/mime/32/empty.png" height="32" width="32" alt="25edochorale.mid" /&gt;&lt;/a&gt;&lt;div&gt;&lt;a href="/file/view/25edochorale.mid/314425794/25edochorale.mid" onclick="ws.common.trackFileLink('/file/view/25edochorale.mid/314425794/25edochorale.mid');" class="filename" title="25edochorale.mid"&gt;25edochorale.mid&lt;/a&gt;&lt;br /&gt;&lt;ul&gt;&lt;li&gt;&lt;a href="/file/detail/25edochorale.mid"&gt;Details&lt;/a&gt;&lt;/li&gt;&lt;li&gt;&lt;a href="/file/view/25edochorale.mid/314425794/25edochorale.mid"&gt;Download&lt;/a&gt;&lt;/li&gt;&lt;li style="color: #666"&gt;4 KB&lt;/li&gt;&lt;/ul&gt;&lt;/div&gt;&lt;/div&gt;&lt;!-- ws:end:WikiTextFileRule:680 --&gt; Peter Kosmorsky (10/14/10, 2.5.7 subgroup, a friend responded &amp;quot;The &lt;span class="il"&gt;25edo&lt;/span&gt; canon has a nice theme, but all the harmonizations from there are laughably dissonant. I showed them to my roomie and he found it disturbing, hahaha. He had an unintentional physical reaction to it with his mouth in which his muscles did a smirk sort of thing, without him even trying to, hahaha. So, my point; this I think this 25 edo idea was an example of where tonal thinking doesn't suit the sound of the scale.&amp;quot;)&lt;br /&gt;
&lt;!-- ws:start:WikiTextMediaRule:1:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/file-audio/25%20edo%20prelude%20largo.mid?h=50&amp;amp;w=300&amp;quot; class=&amp;quot;WikiMedia WikiMediaFile&amp;quot; id=&amp;quot;wikitext@@media@@type=&amp;amp;quot;file&amp;amp;quot; key=&amp;amp;quot;25 edo prelude largo.mid&amp;amp;quot; width=&amp;amp;quot;300&amp;amp;quot; height=&amp;amp;quot;50&amp;amp;quot;&amp;quot; title=&amp;quot;Local Media File&amp;quot;height=&amp;quot;50&amp;quot; width=&amp;quot;300&amp;quot;/&amp;gt; --&gt;&lt;embed type="audio/midi" style="cursor:hand; cursor:pointer;" src="http://xenharmonic.wikispaces.com/file/view/25+edo+prelude+largo.mid" width="300" height="50" autoplay="false" target="myself" controller="true" loop="false" scale="aspect" bgcolor="#FFFFFF" pluginspage="http://www.apple.com/quicktime/download/"&gt;&lt;/embed&gt;&lt;!-- ws:end:WikiTextMediaRule:1 --&gt; &lt;!-- ws:start:WikiTextFileRule:681:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/file/25%20edo%20prelude%20largo.mid?h=52&amp;amp;w=320&amp;quot; class=&amp;quot;WikiFile&amp;quot; id=&amp;quot;wikitext@@file@@25 edo prelude largo.mid&amp;quot; title=&amp;quot;File: 25 edo prelude largo.mid&amp;quot; width=&amp;quot;320&amp;quot; height=&amp;quot;52&amp;quot; /&amp;gt; --&gt;&lt;div class="objectEmbed"&gt;&lt;a href="/file/view/25%20edo%20prelude%20largo.mid/314425914/25%20edo%20prelude%20largo.mid" onclick="ws.common.trackFileLink('/file/view/25%20edo%20prelude%20largo.mid/314425914/25%20edo%20prelude%20largo.mid');"&gt;&lt;img src="http://c1.wikicdn.com/i/mime/32/empty.png" height="32" width="32" alt="25 edo prelude largo.mid" /&gt;&lt;/a&gt;&lt;div&gt;&lt;a href="/file/view/25%20edo%20prelude%20largo.mid/314425914/25%20edo%20prelude%20largo.mid" onclick="ws.common.trackFileLink('/file/view/25%20edo%20prelude%20largo.mid/314425914/25%20edo%20prelude%20largo.mid');" class="filename" title="25 edo prelude largo.mid"&gt;25 edo prelude largo.mid&lt;/a&gt;&lt;br /&gt;&lt;ul&gt;&lt;li&gt;&lt;a href="/file/detail/25%20edo%20prelude%20largo.mid"&gt;Details&lt;/a&gt;&lt;/li&gt;&lt;li&gt;&lt;a href="/file/view/25%20edo%20prelude%20largo.mid/314425914/25%20edo%20prelude%20largo.mid"&gt;Download&lt;/a&gt;&lt;/li&gt;&lt;li style="color: #666"&gt;6 KB&lt;/li&gt;&lt;/ul&gt;&lt;/div&gt;&lt;/div&gt;&lt;!-- ws:end:WikiTextFileRule:681 --&gt; Peter Kosmorsky (2011, Blackwood)&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:7:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc2"&gt;&lt;a name="Intervals"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:7 --&gt;Intervals&lt;/h1&gt;
&lt;br /&gt;


=Relationship to Armodue=


&lt;table class="wiki_table"&gt;
Like [[16edo|16-EDO]] and [[23edo|23-EDO]], 25-EDO contains the 9-note "Superdiatonic" scale of [[7L_2s|7L2s]] (LLLsLLLLs) that is generated by a circle of heavily-flattened 3/2s (ranging in size from 5\9-EDO or 666.67 cents, to 4\7-EDO or 685.71 cents). The 25-EDO generator for this scale is the 672-cent interval. This allows 25-EDO to be used with the [[Armodue_theory|Armodue]] notation system in much the same way that [[19edo|19-EDO]] is used with the standard diatonic notation; see the above interval chart for the Armodue names. Because the 25-EDO Armodue 6th is flatter than that of 16-EDO (the middle of the Armodue spectrum), sharps are lower in pitch than enharmonic flats.
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;Degrees&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Cents&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Approximate&lt;br /&gt;
Ratios*&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Armodue&lt;br /&gt;
Notation&lt;br /&gt;
&lt;/td&gt;
        &lt;td colspan="3" style="text-align: center;"&gt;&lt;a class="wiki_link" href="http://xenharmonic.wikispaces.com/Ups%20and%20Downs%20Notation"&gt;ups and downs notation&lt;/a&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;0&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;0&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1/1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;P1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;perfect 1sn&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;D, Eb&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;48&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;33/32, 39/38, 34/33&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^1, ^m2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;up 1sn, upminor 2nd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;D^, Eb^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;96&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;17/16, 20/19, 18/17&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;2b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^^m2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-upminor 2nd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Eb^^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;144&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;12/11, 38/35&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vvM2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-downmajor 2nd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Evv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;192&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;9/8, 10/9, 19/17&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;2#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vM2&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;downmajor 2nd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Ev&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;5·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;240&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;8/7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;3b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;M2, m3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;major 2nd, minor 3rd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;E, F&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;288&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;19/16, 20/17&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^m3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;upminor 3rd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;F^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;336&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;39/32, 17/14, 40/33&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;3#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^^m3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-upminor 3rd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;F^^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;8·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;384&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;5/4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;4b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vvM3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-downmajor 3rd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;F#vv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;9&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;432&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;9/7, 32/25, 50/39&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vM3&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;downmajor&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;F#v&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;10&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;480&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;33/25, 25/19&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;4#/5b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;M3, P4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;major 3rd, perfect 4th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;F#, G&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;11·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;528&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;31/21, 34/25&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;5&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;up 4th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;G^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;12&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;576&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;7/5, 39/28&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;5#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^^4,^^d5&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-up 4th,&lt;br /&gt;
double-up dim 5th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;G^^, Ab^^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;13&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;624&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;10/7, 56/39&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;6b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vvA4,vv5&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-down aug 4th,&lt;br /&gt;
double-down 5th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;G#vv, Avv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;14·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;672&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;42/31, 25/17&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;v5&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;down 5th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Av&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;15&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;720&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;50/33, 38/25&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;6#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;P5, m6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;perfect 5th, minor 6th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;A, Bb&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;16&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;768&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;14/9, 25/16, 39/25&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;7b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^m6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;upminor 6th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Bb^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;17·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;816&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;8/5&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^^m6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-upminor 6th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Bb^^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;18&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;864&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;64/39, 28/17, 33/20&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;7#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vvM6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-downmajor 6th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Bvv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;19&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;912&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;32/19, 17/10&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;8b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vM6&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;downmajor 6th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Bv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;20·&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;960&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;7/4&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;8&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;M6, m7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;major 6th, minor 7th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;B, C&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;21&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1008&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;16/9, 9/5, 34/19&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;8#&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^m7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;upminor 7th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;C^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;22&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1056&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;11/6, 35/19&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;9b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;^^m7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-upminor 7th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;C^^&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;23&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1104&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;32/17, 17/9, 19/10&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;9&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vvM7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;double-downmajor 7th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;C#vv&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;24&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1152&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;33/17, 64/33, 76/39&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;9#/1b&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;vM7&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;downmajor 7th&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;C#v&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;25&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1200&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;2/1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;1&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;P8&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;perfect 8ve&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;C#, D&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
&lt;/table&gt;


*based on treating 25-EDO as a 2.9.5.7.33.39.17.19 subgroup; other approaches are possible.&lt;br /&gt;
=Commas=
&lt;br /&gt;
25 EDO tempers out the following commas. (Note: This assumes the val &lt; 25 40 58 70 86 93 |.)
&lt;!-- ws:start:WikiTextMediaRule:2:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/custom/25100128?h=0&amp;amp;w=0&amp;quot; class=&amp;quot;WikiMedia WikiMediaCustom&amp;quot; id=&amp;quot;wikitext@@media@@type=&amp;amp;quot;custom&amp;amp;quot; key=&amp;amp;quot;25100128&amp;amp;quot;&amp;quot; title=&amp;quot;Custom Media&amp;quot;/&amp;gt; --&gt;&lt;object id="example" type="image/svg+xml" data="http://xenharmonic.wikispaces.com/file/view/25ed2-001.svg"&gt;alt : Your browser has no SVG support.&lt;/object&gt;&lt;!-- ws:end:WikiTextMediaRule:2 --&gt;&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextFileRule:682:&amp;lt;img src=&amp;quot;http://www.wikispaces.com/site/embedthumbnail/file/25ed2-001.svg?h=52&amp;amp;w=320&amp;quot; class=&amp;quot;WikiFile&amp;quot; id=&amp;quot;wikitext@@file@@25ed2-001.svg&amp;quot; title=&amp;quot;File: 25ed2-001.svg&amp;quot; width=&amp;quot;320&amp;quot; height=&amp;quot;52&amp;quot; /&amp;gt; --&gt;&lt;div class="objectEmbed"&gt;&lt;a href="/file/view/25ed2-001.svg/489051424/25ed2-001.svg" onclick="ws.common.trackFileLink('/file/view/25ed2-001.svg/489051424/25ed2-001.svg');"&gt;&lt;img src="http://c1.wikicdn.com/i/mime/32/empty.png" height="32" width="32" alt="25ed2-001.svg" /&gt;&lt;/a&gt;&lt;div&gt;&lt;a href="/file/view/25ed2-001.svg/489051424/25ed2-001.svg" onclick="ws.common.trackFileLink('/file/view/25ed2-001.svg/489051424/25ed2-001.svg');" class="filename" title="25ed2-001.svg"&gt;25ed2-001.svg&lt;/a&gt;&lt;br /&gt;&lt;ul&gt;&lt;li&gt;&lt;a href="/file/detail/25ed2-001.svg"&gt;Details&lt;/a&gt;&lt;/li&gt;&lt;li&gt;&lt;a href="/file/view/25ed2-001.svg/489051424/25ed2-001.svg"&gt;Download&lt;/a&gt;&lt;/li&gt;&lt;li style="color: #666"&gt;23 KB&lt;/li&gt;&lt;/ul&gt;&lt;/div&gt;&lt;/div&gt;&lt;!-- ws:end:WikiTextFileRule:682 --&gt;&lt;br /&gt;
&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:9:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc3"&gt;&lt;a name="Relationship to Armodue"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:9 --&gt;Relationship to Armodue&lt;/h1&gt;
&lt;br /&gt;
Like &lt;a class="wiki_link" href="/16edo"&gt;16-EDO&lt;/a&gt; and &lt;a class="wiki_link" href="/23edo"&gt;23-EDO&lt;/a&gt;, 25-EDO contains the 9-note &amp;quot;Superdiatonic&amp;quot; scale of &lt;a class="wiki_link" href="/7L%202s"&gt;7L2s&lt;/a&gt; (LLLsLLLLs) that is generated by a circle of heavily-flattened 3/2s (ranging in size from 5\9-EDO or 666.67 cents, to 4\7-EDO or 685.71 cents). The 25-EDO generator for this scale is the 672-cent interval. This allows 25-EDO to be used with the &lt;a class="wiki_link" href="/Armodue%20theory"&gt;Armodue&lt;/a&gt; notation system in much the same way that &lt;a class="wiki_link" href="/19edo"&gt;19-EDO&lt;/a&gt; is used with the standard diatonic notation; see the above interval chart for the Armodue names. Because the 25-EDO Armodue 6th is flatter than that of 16-EDO (the middle of the Armodue spectrum), sharps are lower in pitch than enharmonic flats.&lt;br /&gt;
&lt;br /&gt;
&lt;!-- ws:start:WikiTextHeadingRule:11:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc4"&gt;&lt;a name="Commas"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:11 --&gt;Commas&lt;/h1&gt;
25 EDO tempers out the following commas. (Note: This assumes the val &amp;lt; 25 40 58 70 86 93 |.)&lt;br /&gt;


{| class="wikitable"
|-
! | Comma
! | Monzo
! | Value (Cents)
! | Name 1
! | Name 2
! | Name 3
|-
| style="text-align:center;" | 256/243
| | | 8 -5 &gt;
| style="text-align:right;" | 90.22
| style="text-align:center;" | Limma
| style="text-align:center;" | Pythagorean Minor 2nd
| style="text-align:center;" |
|-
| style="text-align:center;" | 3125/3072
| | | -10 -1 5 &gt;
| style="text-align:right;" | 29.61
| style="text-align:center;" | Small Diesis
| style="text-align:center;" | Magic Comma
| style="text-align:center;" |
|-
| style="text-align:center;" |
| | | 38 -2 -15 &gt;
| style="text-align:right;" | 1.38
| style="text-align:center;" | Hemithirds Comma
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 16807/16384
| | | -14 0 0 5 &gt;
| style="text-align:right;" | 44.13
| |
| |
| |
|-
| style="text-align:center;" | 49/48
| | | -4 -1 0 2 &gt;
| style="text-align:right;" | 35.70
| style="text-align:center;" | Slendro Diesis
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 64/63
| | | 6 -2 0 -1 &gt;
| style="text-align:right;" | 27.26
| style="text-align:center;" | Septimal Comma
| style="text-align:center;" | Archytas' Comma
| style="text-align:center;" | Leipziger Komma
|-
| style="text-align:center;" | 3125/3087
| | | 0 -2 5 -3 &gt;
| style="text-align:right;" | 21.18
| style="text-align:center;" | Gariboh
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 50421/50000
| | | -4 1 -5 5 &gt;
| style="text-align:right;" | 14.52
| style="text-align:center;" | Trimyna
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 1029/1024
| | | -10 1 0 3 &gt;
| style="text-align:right;" | 8.43
| style="text-align:center;" | Gamelisma
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 3136/3125
| | | 6 0 -5 2 &gt;
| style="text-align:right;" | 6.08
| style="text-align:center;" | Hemimean
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 65625/65536
| | | -16 1 5 1 &gt;
| style="text-align:right;" | 2.35
| style="text-align:center;" | Horwell
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 100/99
| | | 2 -2 2 0 -1 &gt;
| style="text-align:right;" | 17.40
| style="text-align:center;" | Ptolemisma
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 176/175
| | | 4 0 -2 -1 1 &gt;
| style="text-align:right;" | 9.86
| style="text-align:center;" | Valinorsma
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 91/90
| | | -1 -2 -1 1 0 1 &gt;
| style="text-align:right;" | 19.13
| style="text-align:center;" | Superleap
| style="text-align:center;" |
| style="text-align:center;" |
|-
| style="text-align:center;" | 676/675
| | | 2 -3 -2 0 0 2 &gt;
| style="text-align:right;" | 2.56
| style="text-align:center;" | Parizeksma
| style="text-align:center;" |
| style="text-align:center;" |
|}


&lt;table class="wiki_table"&gt;
=A 25edo keyboard=
    &lt;tr&gt;
        &lt;th&gt;Comma&lt;br /&gt;
&lt;/th&gt;
        &lt;th&gt;Monzo&lt;br /&gt;
&lt;/th&gt;
        &lt;th&gt;Value (Cents)&lt;br /&gt;
&lt;/th&gt;
        &lt;th&gt;Name 1&lt;br /&gt;
&lt;/th&gt;
        &lt;th&gt;Name 2&lt;br /&gt;
&lt;/th&gt;
        &lt;th&gt;Name 3&lt;br /&gt;
&lt;/th&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;256/243&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 8 -5 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;90.22&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Limma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Pythagorean Minor 2nd&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;3125/3072&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -10 -1 5 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;29.61&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Small Diesis&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Magic Comma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 38 -2 -15 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;1.38&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Hemithirds Comma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;16807/16384&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;| -14 0 0 5 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;44.13&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;49/48&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -4 -1 0 2 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;35.70&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Slendro Diesis&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;64/63&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 6 -2 0 -1 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;27.26&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Septimal Comma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Archytas' Comma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Leipziger Komma&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;3125/3087&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 0 -2 5 -3 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;21.18&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Gariboh&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;50421/50000&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -4 1 -5 5 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;14.52&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Trimyna&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;1029/1024&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -10 1 0 3 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;8.43&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Gamelisma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;3136/3125&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 6 0 -5 2 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;6.08&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Hemimean&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;65625/65536&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -16 1 5 1 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;2.35&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Horwell&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;100/99&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 2 -2 2 0 -1 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;17.40&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Ptolemisma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;176/175&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 4 0 -2 -1 1 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;9.86&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Valinorsma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;91/90&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| -1 -2 -1 1 0 1 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;19.13&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Superleap&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
    &lt;tr&gt;
        &lt;td style="text-align: center;"&gt;676/675&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: left;"&gt;| 2 -3 -2 0 0 2 &amp;gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: right;"&gt;2.56&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;Parizeksma&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
        &lt;td style="text-align: center;"&gt;&lt;br /&gt;
&lt;/td&gt;
    &lt;/tr&gt;
&lt;/table&gt;


&lt;br /&gt;
[[File:mm25.PNG|alt=mm25.PNG|mm25.PNG]]      [[Category:25edo]]
&lt;!-- ws:start:WikiTextHeadingRule:13:&amp;lt;h1&amp;gt; --&gt;&lt;h1 id="toc5"&gt;&lt;a name="A 25edo keyboard"&gt;&lt;/a&gt;&lt;!-- ws:end:WikiTextHeadingRule:13 --&gt;A 25edo keyboard&lt;/h1&gt;
[[Category:edo]]
&lt;br /&gt;
[[Category:keyboard]]
&lt;!-- ws:start:WikiTextLocalImageRule:679:&amp;lt;img src=&amp;quot;/file/view/mm25.PNG/179204243/mm25.PNG&amp;quot; alt=&amp;quot;&amp;quot; title=&amp;quot;&amp;quot; /&amp;gt; --&gt;&lt;img src="/file/view/mm25.PNG/179204243/mm25.PNG" alt="mm25.PNG" title="mm25.PNG" /&gt;&lt;!-- ws:end:WikiTextLocalImageRule:679 --&gt;&lt;/body&gt;&lt;/html&gt;</pre></div>
[[Category:listen]]
[[Category:subgroup]]
[[Category:todo:unify_precision]]
[[Category:twentuning]]

Revision as of 00:00, 17 July 2018

25 tone equal temperament

25EDO divides the octave in 25 equal steps of exact size 48 cents each. It is a good way to tune the Blackwood temperament, which takes the very sharp fifths of 5EDO as a given, tempers out 28/27 and 49/48, and attempts to optimize the tunings for 5 (5/4) and 7 (7/4). It also tunes sixix temperament with a sharp fifth. It supplies the optimal patent val for the 11-limit 6&25 temperament tempering out 49/48, 77/75 and 605/576, and the 13-limit extension also tempering out 66/65.

25EDO has fifths 18 cents sharp, but its major thirds are excellent and its 7/4 is acceptable. Moreover, in full 7-limit including the 3, it is not consistent. It therefore makes sense to use it as a 2.5.7 subgroup tuning. Looking just at 2, 5, and 7, it equates five 8/7s with the octave, and so tempers out (8/7)^5 / 2 = 16807/16384. It also equates a 128/125 diesis and two septimal tritones of 7/5 with the octave, and hence tempers out 3136/3125. If we want to temper out both of these and also have decent fifths, the obvious solution is 50EDO. An alternative fifth, 14\25, which is 672 cents, provides an alternative very flat fifth which can be used for mavila temperament.

If 5/4 and 7/4 aren't good enough, it also does 17/16 and 19/16, just like 12EDO. In fact, on the 2*25 subgroup 2.9.5.7.33.39.17.19 it provides the same tuning and tempers out the same commas as 50et, which makes for a wide range of harmony.

Music

Study in Fives by Paul Rapoport

Fantasy for Piano in 25 Note per Octave Tuning play by Chris Vaisvil

Flat fourth blues by Fabrizio Fulvio Fausto Fiale

File:25edochorale.mid 25edochorale.mid Peter Kosmorsky (10/14/10, 2.5.7 subgroup, a friend responded "The 25edo canon has a nice theme, but all the harmonizations from there are laughably dissonant. I showed them to my roomie and he found it disturbing, hahaha. He had an unintentional physical reaction to it with his mouth in which his muscles did a smirk sort of thing, without him even trying to, hahaha. So, my point; this I think this 25 edo idea was an example of where tonal thinking doesn't suit the sound of the scale.")

File:25 edo prelude largo.mid 25 edo prelude largo.mid Peter Kosmorsky (2011, Blackwood)

Intervals

Degrees Cents Approximate

Ratios*

Armodue

Notation

ups and downs notation
0 0 1/1 1 P1 perfect 1sn D, Eb
1 48 33/32, 39/38, 34/33 1# ^1, ^m2 up 1sn, upminor 2nd D^, Eb^
2 96 17/16, 20/19, 18/17 2b ^^m2 double-upminor 2nd Eb^^
3 144 12/11, 38/35 2 vvM2 double-downmajor 2nd Evv
4 192 9/8, 10/9, 19/17 2# vM2 downmajor 2nd Ev
5· 240 8/7 3b M2, m3 major 2nd, minor 3rd E, F
6 288 19/16, 20/17 3 ^m3 upminor 3rd F^
7 336 39/32, 17/14, 40/33 3# ^^m3 double-upminor 3rd F^^
8· 384 5/4 4b vvM3 double-downmajor 3rd F#vv
9 432 9/7, 32/25, 50/39 4 vM3 downmajor F#v
10 480 33/25, 25/19 4#/5b M3, P4 major 3rd, perfect 4th F#, G
11· 528 31/21, 34/25 5 ^4 up 4th G^
12 576 7/5, 39/28 5# ^^4,^^d5 double-up 4th,

double-up dim 5th

G^^, Ab^^
13 624 10/7, 56/39 6b vvA4,vv5 double-down aug 4th,

double-down 5th

G#vv, Avv
14· 672 42/31, 25/17 6 v5 down 5th Av
15 720 50/33, 38/25 6# P5, m6 perfect 5th, minor 6th A, Bb
16 768 14/9, 25/16, 39/25 7b ^m6 upminor 6th Bb^
17· 816 8/5 7 ^^m6 double-upminor 6th Bb^^
18 864 64/39, 28/17, 33/20 7# vvM6 double-downmajor 6th Bvv
19 912 32/19, 17/10 8b vM6 downmajor 6th Bv
20· 960 7/4 8 M6, m7 major 6th, minor 7th B, C
21 1008 16/9, 9/5, 34/19 8# ^m7 upminor 7th C^
22 1056 11/6, 35/19 9b ^^m7 double-upminor 7th C^^
23 1104 32/17, 17/9, 19/10 9 vvM7 double-downmajor 7th C#vv
24 1152 33/17, 64/33, 76/39 9#/1b vM7 downmajor 7th C#v
25 1200 2/1 1 P8 perfect 8ve C#, D
  • based on treating 25-EDO as a 2.9.5.7.33.39.17.19 subgroup; other approaches are possible.

alt : Your browser has no SVG support.

25ed2-001.svg

Relationship to Armodue

Like 16-EDO and 23-EDO, 25-EDO contains the 9-note "Superdiatonic" scale of 7L2s (LLLsLLLLs) that is generated by a circle of heavily-flattened 3/2s (ranging in size from 5\9-EDO or 666.67 cents, to 4\7-EDO or 685.71 cents). The 25-EDO generator for this scale is the 672-cent interval. This allows 25-EDO to be used with the Armodue notation system in much the same way that 19-EDO is used with the standard diatonic notation; see the above interval chart for the Armodue names. Because the 25-EDO Armodue 6th is flatter than that of 16-EDO (the middle of the Armodue spectrum), sharps are lower in pitch than enharmonic flats.

Commas

25 EDO tempers out the following commas. (Note: This assumes the val < 25 40 58 70 86 93 |.)

Comma Monzo Value (Cents) Name 1 Name 2 Name 3
256/243 | 8 -5 > 90.22 Limma Pythagorean Minor 2nd
3125/3072 | -10 -1 5 > 29.61 Small Diesis Magic Comma
| 38 -2 -15 > 1.38 Hemithirds Comma
16807/16384 | -14 0 0 5 > 44.13
49/48 | -4 -1 0 2 > 35.70 Slendro Diesis
64/63 | 6 -2 0 -1 > 27.26 Septimal Comma Archytas' Comma Leipziger Komma
3125/3087 | 0 -2 5 -3 > 21.18 Gariboh
50421/50000 | -4 1 -5 5 > 14.52 Trimyna
1029/1024 | -10 1 0 3 > 8.43 Gamelisma
3136/3125 | 6 0 -5 2 > 6.08 Hemimean
65625/65536 | -16 1 5 1 > 2.35 Horwell
100/99 | 2 -2 2 0 -1 > 17.40 Ptolemisma
176/175 | 4 0 -2 -1 1 > 9.86 Valinorsma
91/90 | -1 -2 -1 1 0 1 > 19.13 Superleap
676/675 | 2 -3 -2 0 0 2 > 2.56 Parizeksma

A 25edo keyboard

mm25.PNG

Retrieved from "https://en.xen.wiki/index.php?title=25edo&oldid=522"