User:VectorGraphics/Delkian scale: Difference between revisions
tgwe |
e |
||
| Line 36: | Line 36: | ||
| rowspan="2" |1st | | rowspan="2" |1st | ||
|minor 1st | |minor 1st | ||
| | |tertigrade | ||
|s | |s | ||
|2 | |2 | ||
| Line 43: | Line 43: | ||
|major minor 2nd | |major minor 2nd | ||
|major 1st | |major 1st | ||
| | |semigrade | ||
|L | |L | ||
|3 | |3 | ||
| Line 52: | Line 52: | ||
| rowspan="2" |2nd | | rowspan="2" |2nd | ||
|minor 2nd | |minor 2nd | ||
| | |greater digrade | ||
|L+s | |L+s | ||
|5 | |5 | ||
| Line 59: | Line 59: | ||
|major major 2nd | |major major 2nd | ||
|major 2nd | |major 2nd | ||
| | |lacuna | ||
|2L | |2L | ||
|6 | |6 | ||
| Line 68: | Line 68: | ||
| rowspan="2" |3rd | | rowspan="2" |3rd | ||
|minor 3rd | |minor 3rd | ||
| | |prequadrant | ||
|2L+s | |2L+s | ||
|8 | |8 | ||
| Line 75: | Line 75: | ||
|major minor 3rd | |major minor 3rd | ||
|major 3rd | |major 3rd | ||
| | |quadrant | ||
|3L | |3L | ||
|9 | |9 | ||
| Line 91: | Line 91: | ||
|major major 3rd | |major major 3rd | ||
|major 4th | |major 4th | ||
| | |bilacuna | ||
|4L | |4L | ||
|12 | |12 | ||
| Line 100: | Line 100: | ||
| rowspan="2" |5th | | rowspan="2" |5th | ||
|perfect 5th | |perfect 5th | ||
| | |tersquance | ||
|4L+s | |4L+s | ||
|14 | |14 | ||
| Line 123: | Line 123: | ||
|perfect tritone | |perfect tritone | ||
|perfect 6th | |perfect 6th | ||
| | |median | ||
|5L+s | |5L+s | ||
|17 | |17 | ||
| Line 146: | Line 146: | ||
|perfect 5th | |perfect 5th | ||
|perfect 7th | |perfect 7th | ||
| | |sesquance | ||
|6L+s | |6L+s | ||
|20 | |20 | ||
| Line 155: | Line 155: | ||
| rowspan="2" |8th | | rowspan="2" |8th | ||
|minor 8th | |minor 8th | ||
| | |antibilacuna | ||
|6L+2s | |6L+2s | ||
|22 | |22 | ||
| Line 171: | Line 171: | ||
| rowspan="2" |9th | | rowspan="2" |9th | ||
|minor 9th | |minor 9th | ||
| | |dodrant | ||
|7L+2s | |7L+2s | ||
|25 | |25 | ||
| Line 178: | Line 178: | ||
|major major 6th | |major major 6th | ||
|major 9th | |major 9th | ||
| | |postdodrant | ||
|8L+s | |8L+s | ||
|26 | |26 | ||
| Line 187: | Line 187: | ||
| rowspan="2" |10th | | rowspan="2" |10th | ||
|minor 10th | |minor 10th | ||
| | |antilacuna | ||
|8L+2s | |8L+2s | ||
|28 | |28 | ||
| Line 194: | Line 194: | ||
|major minor 7th | |major minor 7th | ||
|major 10th | |major 10th | ||
| | |greater antidigrade | ||
|9L+s | |9L+s | ||
|29 | |29 | ||
| Line 203: | Line 203: | ||
| rowspan="2" |11th | | rowspan="2" |11th | ||
|minor 11th | |minor 11th | ||
| | |antisemigrade | ||
|9L+2s | |9L+2s | ||
|31 | |31 | ||
| Line 210: | Line 210: | ||
|major major 7th | |major major 7th | ||
|major 11th | |major 11th | ||
| | |antitertigrade | ||
|10L+s | |10L+s | ||
|32 | |32 | ||
| Line 219: | Line 219: | ||
|12th | |12th | ||
|perfect 12th | |perfect 12th | ||
| | |duplance | ||
|10L+2s | |10L+2s | ||
|34 | |34 | ||
Revision as of 20:33, 7 July 2024
This is about the 34edo scale called "diatonic" in the fictional universe it's used in. For the MOS equivalent, see 10L 2s. For normal diatonic tuning in 34edo, see 34edo (internal link, I just don't know how to link to a specific section).
The Delkian scale is a scale used in Majestaz's Famana, with 12 notes: it is an octave-equivalent scale containing 10 large steps and 2 small steps. The small steps are unevenly spaced, with a pattern of LLLLsLLLLLLs, as such it is not formed by a generator, though 10 of its 12 degrees have a perfect fifth above them.
Name
The Delkian scale is referred to as "diatonic" in the fictional universe of Famana, as the 5L 2S diatonic of Western music theory is not used. It is called the "Delkian diatonic" due to an alternative popular tuning system called the Roklotian diatonic.
Notation
Intervals
Each interval class of the Delkian scale corresponds to an edostep of 12edo, just as each 12edo interval class corresponds to an edostep of 7edo. Each interval has 2 sizes, except for the tritone, which has 3.
| Generic name (Western) | Specific name (Western) | Generic name (translated; in-universe) | Specific name (translated; in-universe) | Special name (in-universe) | Steps subtended | Size in 34-edosteps (34 edo) | Note name (starting on N) |
|---|---|---|---|---|---|---|---|
| unison | perfect unison | unison | perfect unison | 0 | 0 | N | |
| minor 2nd | minor minor 2nd | 1st | minor 1st | tertigrade | s | 2 | F- |
| major minor 2nd | major 1st | semigrade | L | 3 | F | ||
| major 2nd | minor major 2nd | 2nd | minor 2nd | greater digrade | L+s | 5 | S- |
| major major 2nd | major 2nd | lacuna | 2L | 6 | S | ||
| minor 3rd | minor minor 3rd | 3rd | minor 3rd | prequadrant | 2L+s | 8 | Z- |
| major minor 3rd | major 3rd | quadrant | 3L | 9 | Z | ||
| major 3rd | minor major 3rd | 4th | minor 4th | terce | 3L+s | 11 | G |
| major major 3rd | major 4th | bilacuna | 4L | 12 | G+ | ||
| 4th | perfect 4th | 5th | perfect 5th | tersquance | 4L+s | 14 | X |
| augmented 4th | augmented 5th | 5L | 15 | X+ | |||
| tritone | diminished tritone | 6th | diminished 6th | 4L+2s | 16 | V- | |
| perfect tritone | perfect 6th | median | 5L+s | 17 | V | ||
| augmented tritone | augmented 6th | 6L | 18 | V+ | |||
| 5th | diminished 5th | 7th | diminished 7th | 5L+2s | 19 | M- | |
| perfect 5th | perfect 7th | sesquance | 6L+s | 20 | M | ||
| minor 6th | minor minor 6th | 8th | minor 8th | antibilacuna | 6L+2s | 22 | P- |
| major minor 6th | major 8th | bess | 7L+s | 23 | P | ||
| major 6th | minor major 6th | 9th | minor 9th | dodrant | 7L+2s | 25 | T |
| major major 6th | major 9th | postdodrant | 8L+s | 26 | T+ | ||
| minor 7th | minor minor 7th | 10th | minor 10th | antilacuna | 8L+2s | 28 | C |
| major minor 7th | major 10th | greater antidigrade | 9L+s | 29 | C+ | ||
| major 7th | minor major 7th | 11th | minor 11th | antisemigrade | 9L+2s | 31 | W |
| major major 7th | major 11th | antitertigrade | 10L+s | 32 | W+ | ||
| octave | perfect octave | 12th | perfect 12th | duplance | 10L+2s | 34 | N |
Note names
There are 12 base notes: N, F, S, Z, G, X, V/L (in equal-tempered tuning, these are the same note), M, P, T, C, and W, and then back to N. These are consonants found in a language spoken in the fictional setting. There are two accidentals: - and +. + raises the pitch, and - lowers it, by one chroma. In-universe, this is analyzed as simply a small change in pitch, unlike our # and b, which are generalized based on fifth stacking.
Theory
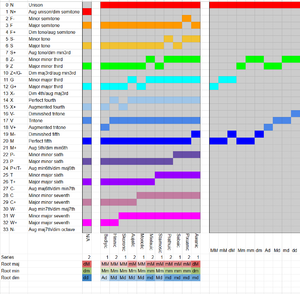
The key features of the scale are that you now get both major and minor thirds in any given key, which can be either 17edo's more extreme thirds, or the more just thirds 34edo provides, or some mix of the options. These comma-sized variations in the intervals define the mode's distinct feel.
The scale was created taking both 3 and 5 into account. Naturally, the main harmonic tool is not a chain of fifths but rather a harmonic table of fifths and classical major thirds, as follows (described in terms of 34-edosteps here, with the Staimosic mode highlighted):
| 22 | 8 | 28 | 14 | 0 | 20 | 6 | 26 | 12 | 32 | 18 | 4 | 24 | 10 | 30 | 16 | 2 |
| 33 | 19 | 5 | 25 | 11 | 31 | 17 | 3 | 23 | 9 | 29 | 15 | 1 | 21 | 7 | 27 | 13 |
| 10 | 30 | 16 | 2 | 22 | 8 | 28 | 14 | 0 | 20 | 6 | 26 | 12 | 32 | 18 | 4 | 24 |
| 21 | 7 | 27 | 13 | 33 | 19 | 5 | 25 | 11 | 31 | 17 | 3 | 23 | 9 | 29 | 15 | 1 |
| 32 | 18 | 4 | 24 | 10 | 30 | 16 | 2 | 22 | 8 | 28 | 14 | 0 | 20 | 6 | 26 | 12 |
| 9 | 29 | 15 | 1 | 21 | 7 | 27 | 13 | 33 | 19 | 5 | 25 | 11 | 31 | 17 | 3 | 23 |
| 20 | 6 | 26 | 12 | 32 | 18 | 4 | 24 | 10 | 30 | 16 | 2 | 22 | 8 | 28 | 14 | 0 |
| 31 | 17 | 3 | 23 | 9 | 29 | 15 | 1 | 21 | 7 | 27 | 13 | 33 | 19 | 5 | 25 | 11 |
Note that a fifth can be built from 8 stacked 11-step thirds, so this table can be read column-by-column to count up by thirds. Note that fifths never cycle around to create a classical third ("minor major third"), so they just loop around the sides normally.
Additionally, note that multiple wolf fifths are necessary to cycle around the scale, these are just considered a variant of fifth (the "diminished fifth/seventh" mentioned) in-universe.
Modes
11 of the modes of the scale are used in traditional music composition and thus have names. These names are based on ancient tribes from the Famana setting:
| Awanic | LsLLLLsLLLLL |
| Pixuanic | sLLLLLLsLLLL |
| Sebaic | LLsLLLLsLLLL |
| Prathuic | LsLLLLLLsLLL |
| Staimosic | LLLsLLLLsLLL |
| Mielauic | LLsLLLLLLsLL |
| Moriolic | LLLLsLLLLsLL |
| Aujalic | LLLsLLLLLLsL |
| Skoronic | LLLLLsLLLLsL |
| Hininic | LLLLsLLLLLLs |
| Bediyic | LLLLLLsLLLLs |
| N/A | sLLLLsLLLLLL |