Tonality diamond

From Xenharmonic Wiki
Jump to navigation Jump to search
English Wikipedia has an article on:


A tonality diamond is a symmetric organization of otonal and utonal chords based around a central note and bounded by an odd-limit. First formalized in the 7-odd-limit by Max F. Meyer in 1929,[1] the idea became central to the music and theories of Harry Partch,[2] who built his tonal system around the 11-odd-limit tonality diamond. Tonality diamonds have been used both conceptually (such as for targets of temperaments) and practically (such as for instrument layouts) in xenharmonics ever since.

Play some tonality diamonds on your browser here.

Construction

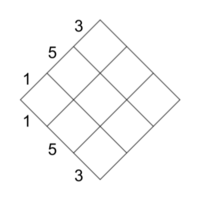
  • Step 1: Take the numbers of an odd-limit and arrange them along two axes.
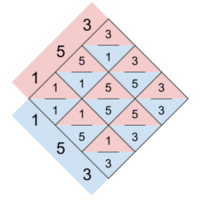
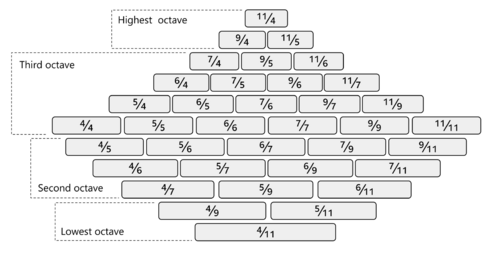
    Step 1: Take the numbers of an odd-limit and arrange them along two axes.
  • Step 2: Using one axis as the numerator and the other as the denominator, fill in the cells with the ratios they form.
    Step 2: Using one axis as the numerator and the other as the denominator, fill in the cells with the ratios they form.
  • Step 3: Octave-reduce the ratios (i.e. make sure the decimal form of each ratio is between 1 and 2; if it is not, double one of the numbers until it is).
    Step 3: Octave-reduce the ratios (i.e. make sure the decimal form of each ratio is between 1 and 2; if it is not, double one of the numbers until it is).
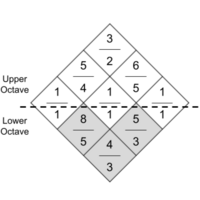
  • Optional step: to make the rows play rooted chords, one half of the diamond (not including the middle unison row) must be lowered by an octave (represented by grey cells in image).
    Optional step: to make the rows play rooted chords, one half of the diamond (not including the middle unison row) must be lowered by an octave (represented by grey cells in image).

Note: the numbers of the odd-limit are generally arranged in one of three ways:

  • Numerically: (1, 3, 5, 7, 9, 11) as in Meyer's 7-limit diamond.
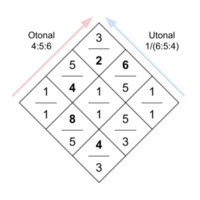
  • Tonally: (1, 9, 5, 11, 3, 7) as in Partch's 11-limit diamond.
  • Chordally: (1, 5, 3, 7, 9, 11) as in the layout for the Diamond Marimba. This creates a 4:5:6:7:9:11 extended 11th chord on the diagonal, arranged in thirds.

Here's a short video illustrating the interlocking nature of the otonal and utonal chords and constant presence of the 1/1 interval in the 5-limit tonality diamond:

Load video
Local File

History

The tonality diamond was first formally explained by Max F. Meyer in his 1929 publication The Musician's Arithmetic using the 7-odd-limit.[1]

Harry Partch is the person most associated with the tonality diamond, and claimed to have invented it. However, it is likely that he plagarized the idea from Meyer.[3] Regardless, his extending of the concept to the 11-odd-limit (as well as his other extensions and uses of it) was an extremely important and foundational moment in the history of xenharmonic music.

Erv Wilson in particular was inspired by Partch's use of the tonality diamond and it's extended form. He developed a number of "diamonds" himself,[4] as well as other concepts inspired by Partch's use of the extended tonality diamond such as constant structure.[5] A related idea of Wilson's is the cross-set, of which the tonality diamond is a special case.

The first novel xenharmonic temperament—George Secor's later-named Miracle temperament—was made to approximate Partch's 11-limit diamond.[6][7]

Instrument layout

The most famous example of the tonality diamond as a practical layout for an instrument is Harry Partch's "Diamond Marimba," which uses the 11-odd-limit tonality diamond exactly. This idea was explored further with Partch's "Quadrangularis Reversum," and by Cris Forster with his 13-odd-limit Diamond Marimba.[8]

Layout of the Diamond Marimba. Ratios are shown unreduced to highlight the structure. Click here to play the Diamond Marimba on your browser.

Music

Banjo Boogie
Cris Forster
Harry Partch
David Paulick
T.J Troy

Related scales

See also

External links

References

  1. ↑ 1.0 1.1 Meyer, Max F. (1929) The Musician’s Arithmetic: Drill Problems for an Introduction to the Scientific Study of Musical Composition. The University of Missouri Studies. Vol. 4, no. 1. University of Missouri. January 1, 1929. p. 22.
  2. ↑ Harry Partch (1949), Genesis of a Music, University of Wisconsin Press
  3. ↑ Forster, Cris (2015). The Partch Hoax Doctrines. Self-published.
  4. ↑ Wilson, Erv. (1965-1970) Letters on Diamond Lattices (PDF) Self-published.
  5. ↑ Wilson, Erv. (1964-2002) The Partch Papers (collection of documents on Harry Partch's 11-limit diamond and its extensions, PDF). Self-published.
  6. ↑ Secor, George (1975). A New Look at the Partch Monophonic Fabric. Xenharmonicon. Vol. 3
  7. ↑ Secor, George. (2006) The Miracle Temperament and Decimal Keyboard. Xenharmonikon. Vol. 18. 2006. pp. 5–15
  8. ↑ https://web.archive.org/web/20220901100217/https://www.chrysalis-foundation.org/instruments-and-music/diamond-marimba-i/
Retrieved from "https://en.xen.wiki/index.php?title=Tonality_diamond&oldid=197981"