User:Squib
todo: some stuff
list of things that i think could be improved about the wiki
My opinion is subject to change. For now, I'm not putting too much thought into this, so don't take anything to heart. Although you probably shouldn't anyway; I'm one person.
- things on this wiki can be very hard to understand
- it's hard to find a page you're looking for even if you know what it's about
- probably something else i forgot
unnamed music theory
A number of things bother me about the way tuning is done on this wiki and in general, in particular octave/tritave equivalence, generators, and the excessive use of hard-to-understand vocabulary and math which often isn't even all that relevant or helpful. The last one should not be a surprise; the first two might be. I find generators extremely unintuitive, and while they may be useful for things, that does not mean I have to like them. I also dislike the concept of equivalence in general. I think *every* pitch should be considered its own thing.
So I decided to formalize the ideas that I have been exploring into a music theory, inspired by Shastavistic music theory.
Terms
Most of these terms are widely-used but I might be using them slightly differently than most people.
Interval: The frequency ratio between two notes. Can be a measurement of specific notes or just a ratio.
Harmonic: An interval which is an integer ratio (including 1/1). Also, a note which is a harmonic interval above another note.
Harmonic Series: The set of notes which are harmonics of the fundamental, including the fundamental itself.
Overtone: A tone produced with the fundamental, contributing to the timbre of a single note.
Explanation
The simplest interval is the unison, 1/1. This is the interval between a note and itself. Stacking it multiple times doesn't do anything, which isn't very interesting, so let's consider the next simplest interval: the octave, 2/1. Although notes an octave apart are not considered equivalent, they do have a special relationship: the higher note is a harmonic of the lower. 3/1 is also a harmonic interval. Stacking these gives us intervals like 4/1, 6/1, and 8/1, which are also harmonics. Since only harmonics can be created, this does not allow for much progression, since every note only contains overtones from the root note. So we will now allow intervals to be subtracted from each other, creating nonharmonic intervals like 3/2 which have new overtones. Going up by harmonics removes some overtones and strengthens the remaining ones; going down by harmonics weakens existing overtones and adds new ones in the gaps. Combining these gives us nonharmonic intervals, and stacking them adds more and more new overtones.
Every culture's music is influenced by the tools available to them. The primary tool available to me is a Launchpad with a 9x9 grid of LED buttons (minus the top right corner). So, the most immediately obvious set of pitches to use is a lattice where moving one button to the right is by 2/1 and one button up is 3/1. This theoretically allows these intervals to be combined in any combination.
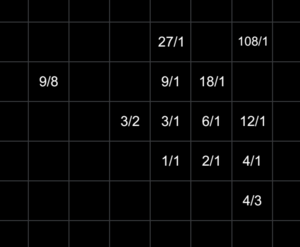
There's a problem. 9/8, the whole tone, is as easy to reach as 108/1! Not only does this make useful intervals like 9/8 more difficult to use, but since keyboard space is limited, this adds extremely high and low notes that render much of the space unusable. So instead, notes can be represented as any combination of fourths (4/3) and fifths (3/2), the two simplest non-harmonic intervals. This leaves 2/1 and 3/1 easily accessible while moving very large intervals further away, as well as moving more complex smaller intervals closer together. It's also much more natural to think of 9/8 as the difference between a fourth and a fifth than it is to think of it as the difference between three 2/1s and two 3/1s, for example.

Thus, the fourths-fifths layout is the most basic layout of this music theory, and it works very well. Except for absolute pitch, every place on the keyboard is the same, a property called isomorphism. This allows any interval or chord to be placed anywhere on the keyboard.
But what about ratios involving 5? 4 can be created from 2×2, and 6 can be created from 2×3, but 5 is prime. It could be represented using a third dimension, but that would be difficult to visualize and next to impossible to play, since most keyboards are at most 2-dimensional, including the Launchpad. So how can we get more notes?
One way is to use the notes we already have. Two 9/8s make a very rough approximation of a major third, but two 4/3s minus three 9/8s is a much closer one and is nearly indistinguishable from 5/4. It's awkward to use, but we can adjust the layout to change that.

Just like when the layout was changed to fourths and fifths, bringing more complex intervals closer pushes larger intervals further away, but this time the range is reduced to only a couple octaves and the intervals far to the side are very complex and not very useful. We can make convenient ether very large or very complex intervals, but not both. The layout shown is in my opinion the best trade-off; it's possible to make 5/4 and especially 10/9 more convenient, but then it can barely fit a single 3/1! So is there a less complex way to approximate 5?
The other way to approximate 5/4 is to indeed add more notes between the existing ones. The tuning we already have is called Pythagorean tuning because it uses only ratios of 2 and 3. We can take two sets of Pythagorean and put them together. There are an infinite number of ways to do this, but only 3 preserve isomorphism. In fact, the number of equal tunings with N sets of pythagorean is exactly equal to the sum of the unique factors of N. Don't ask me why, although I suspect figuring it out will help me name them.
Explanation (that I don't entirely understand) from a mathy discord server I'm in: "These arrangements of n integer lattices must be lattices themselves, so they have a basis. As a basis, we can take {(a,0), (b,c)}, where a is the least positive value such that (a,0) is in the lattice, c is the least positive value such that (x,c) is in the lattice for some x, and b is the least nonnegative value such that (b,c) is in the lattice. a has to be 1/k for integer k because (0,1) is in the lattice, and since the lattice has n copies of the integer lattice, k must be a divisor of n. This means there are n/k integer lattices with points on the x-axis, so c must be k/n. In order for the lattice to close, b must be i/n for some integer i, and since b is minimal, 0 ≤ i/n < 1/k, so 0 ≤ i < n/k and there are n/k possible values of i. Since all divisors of n are of the form n/k for some k | n, the number of lattices is the sum of the divisors of n."
Overview
For now, this is just a list of the things I want to explain here.
- intro
- what this is & why i made it
- how much i'm taking credit for
- no, i don't expect this to become widely-used. although that would be cool.
- philosophy
- creating the theory based on experience and what actually works/is helpful
- intentionally keeping it simple; this makes it more useful even if it's not what i would naturally gravitate to otherwise
- as a result of this: models emerge!
- models are abstractions, describing the important attributes of a complex phenomenon in a simple way.
- the foundation
- what are notes, anyway?
- harmonic series as a model of complex timbres
- overtones as a model of consonance, harmony, and progression
- rational numbers as a model of intervals
- chords & the harmonic series
- why chords are a useful but incomplete model of harmony
- why harmonic series segments are a useful but incomplete model of chords
- so what do we do? keep reading to find out :)
- 2d tunings & layouts
- limited space & the tradeoff between complexity and range
- 3d tunings in a 2d space