User:PiotrGrochowski/Ups and Downs Notation-a
A 22edo example
Ups and Downs is a generic notation system that works with edos with a fifth. It only adds 2 symbols to standard notation, so it's very easy to learn. The name comes from the up symbol "^" and the down symbol "v". When extended with highs and lows, it works with almost all rank 2 tunings (see the pergens page).
It's not created by anyone, it's a mathematical miracle, just like the edos.
To understand the ups and downs notation, let's start with an EDO that doesn't need it. 19-EDO is easy to notate because 7 fifths reduced by 4 octaves adds up to one EDO-step. So C# is right next to C, and the keyboard runs C C# Db D D# Eb E etc. Conventional notation works perfectly with 19-EDO as long as you remember that C# and Db are different notes.
In contrast, 22-EDO is hard to notate because 7 fifths are three EDO-steps, and the usual chain of fifths Eb-Bb-F-C-G-D-A-E-B-F#-C# etc. creates the scale C Db B# C# D Eb Fb D# E F. That's very confusing because B#-Db looks ascending on the page but sounds descending. Also a 4:5:6 chord is written C-D#-G, and the major 3rd becomes an aug 2nd. Some people forgo the chain of fifths for a maximally even scale like C _ _ D _ _ E _ _ F _ _ _ G _ _ A _ _ B _ _ C. But that's confusing because G-D and A-E are dim 5ths. And if your piece is in G or A, that's really bad. A notation system should work in every key!
The solution is to use the sharp symbol to mean "raised by 7 fifths", and to use the up symbol "^" to mean "sharpened by one EDO-step". 22-EDO can be written C - Db - Db^ - Dv - D - Eb - Eb^ - Ev - E - F etc. The notes are pronounced "D-flat-up, D-down", etc. Now the notes run in order. There's a pattern that's not too hard to pick up on, if you remember that there's 3 ups to a sharp.
The names change depending on the key, just like in conventional notation where F# in D major becomes Gb in Db major. So the B scale is B - C - C^ - C#v - C# - D - D^ - D#v - D# - E etc.
The advantage to this notation is that you always know where your fifth is. And hence your 4th, and your major 9th, hence the maj 2nd and the min 7th too. You have convenient landmarks to find your way around, built into the notation. The notation is a map of unfamiliar territory, and we want this map to be as easy to read as possible.
Relative notation for 22-EDO is P1 - m2 - ^m2 - vM2 - M2 - m3 - ^m3 - vM3 - M3 - P4 - d5 - ^d5 - vP5 - P5 etc. That's pronounced "upminor 2nd, downmajor 3rd", etc. The ups and downs are leading in relative notation but trailing in absolute notation. You can apply this pattern to any key, with certain keys requiring double-sharps or even triple-sharps. The notes without ups or downs always form a chain of fifths.
You can loosely relate the ups and downs to JI: major = red or fifthward white, downmajor = yellow, upminor = green, minor = blue or fourthwards white. Or simply up = green, down = yellow, and mid = white, blue or red. (See Kite's color notation for an explanation of the colors.) These correlations are for 22-EDO only, other EDOs have other correlations.
Conventionally, in C you use D# instead of Eb when you have a Gaug chord. You have the freedom to spell your notes how you like, to make your chords look right. Likewise, in 22-EDO, Db can be spelled C^ or B#v or even B^^ ("B double-up"). However avoid using both C# and Db, as the ascending Db-C# interval appears descending.
Interval arithmetic
22-EDO interval arithmetic works out very neatly. Ups and downs are just added in:
C + M3 = E, C + vM3 = Ev, C^ + M3 = E^
D-F# is a M3, Dv-F#v = M3
M2 + m2 = m3, M2 + ^m2 = ^m3, vM2 + m2 = vm3
Sometimes enharmonic equivalents need to be used. Take this scale:
C Db Db^ Dv D Eb Eb^ Ev E F Gb Gb^ Gv G Ab Ab^ Av A Bb Bb^ Bv B C
Here's our fifths: C-G, Db-Ab, Db^-Ab^, Dv-Av, D-A, etc. Most fifths *look* like fifths and are easy to find. So do the 4ths. Our 4\22 maj 2nds are C-D, Db-Eb, Db^-Eb^, Dv-Ev, D-E, Eb-F, good until we reach Eb^-Gb, which is a major 2nd that is spelled as a downminor 3rd. Here's this scale's chain of 5ths:
Gb^ - Db^ - Ab^ - Eb^ - Bb^ - Gb - Db - Ab - Eb - Bb - F - C - G - D - A - E - B - Gv - Dv - Av - Ev - Bv
The problem is, there are a few places where the sequence of 7 letters breaks, and we actually have runs of 5 letters. This is the essentially pentatonic-friendly nature of 22-EDO asserting itself. By which is meant, 22-EDO pentatonically is like 19-EDO heptatonically, in that ups and downs are not necessary. Here's 22-EDO in pentatonic notation:
chain of "fifths": Gx Dx Ax F# C# G# D# A# F C G D A Fb Cb Gb Db Ab Fbb Cbb Gbb Dbb
scale in C: C C# Dbb Db D D# Dx Fbb Fb F F# Gbb Gb G G# Gx Ab A A# Ax Cbb Cb C
That's an awful lot of sharps and flats, but that does make a neat and tidy notation (except for the Dbb-Gx fifth). And it exists as an alternative, embedded within conventional notation, with a key signature with circled X's on the B and E spots.
So the chain of fifths has a few spots to watch out for. You have to remember that fifths sometimes appear as downminor 6ths, in the form of B-something to G-something. A little tricky, but manageable. Analogous to 12-ET, where G# to Eb is a fifth that looks like a sixth.
Staff Notation
For staff notation, just put an up or down to the left of the note and any standard accidental it might have. All 22 possible keys can be written out. Just as conventionally each black key produces both a sharp key and a flat key (Db major and C# minor), each of the 15 black keys of 22-EDO produces both, and there are 37 possible keys. Double-sharps and double-flats are avoided, as are Fb, Cb, B# and E#. Also Fb^, Cb^, B#v and E#v. This is so that the three black keys between, say, C and D are only notated as some version of C or D, never as some version of B or E. To achieve this, ups and downs are allowed in tonic names and key signatures.
major keys: C, Db, Db^, Dv, D, Eb, Eb^, Ev, E, F, F^, Gb^, Gv, G, Ab, Ab^, Av, A, Bb, Bb^, Bv, B
minor keys: C, C^, C#v, C#, D, D^, Eb^, Ev, E, F, F^, F#v, F#, G, G^, G#v, G#, A, Bb, Bb^, Bv, B
Major keys are almost entirely natural, down, flat or upflat. The one exception is F^ major, needed because Gb major would use Cb. Likewise, minor keys are mostly natural, up, sharp or downsharp. Exceptions: Ev minor for D# minor, and Bv minor for A# minor, to avoid E#. In addition, three minor keys are named to match their relative major. This isn't as strict a rule, and the other names may be used as alternatives. Thus Bb minor and Bb^ minor are preferred over A^ minor and A#v minor, to match their relative majors Db major and Db^ major. Also Eb^ minor is preferred over D#v minor, to match its relative major Gb^ major. These two keys break the rule for naming black keys because they have a Cb^. There is unfortunately no way to notate these keys and follow the rule!
Key signatures:
C major: all natural
Db major: B, E, A, D and G are flat
Db^ major: B, E, A, D and G are upflat, C and F are up
Dv major: F and C are downsharp, G, D, A, E and B are down
D major: F and C are sharp
Eb major: B, E, and A are flat
etc.
C minor: B, E and A are flat
C^ minor: B, E and A are upflat, D, G, C and F are up
C#v minor: F, C, G and D are downsharp, A, E and B are down
C# minor: F, C, G and D are sharp
D minor: B is flat
D^ minor: B is upflat, E, A, D, G, C and F are up
etc.
Other EDOs
The up symbol means "sharpened by one edo-step" in any edo that uses them. The size in cents of the up changes greatly depending on the edo, from 120¢ in 10-edo to ~17¢ in 72-edo. The sharp symbol's cents size also depends on the edo, ranging from 240¢ in 5-edo to ~26¢ in 47edo.
EDOs come in 5 categories, based on the size of the fifth. From widest to narrowest:
supersharp = EDOs with fifths wider than 720¢
pentatonic = EDOs with a fifth =720¢
regular = EDOs with a fifth that hits the "sweet spot" between 720¢ and 686¢
perfect =`**`**EDOs with a fifth four sevenths of an octave = 4\7 =`` 686¢
superflat = EDOs with a fifth less than 686¢
This is in addition to the trivial EDOs, 2, 3, 4 and 6, which can be notated with standard notation as a subset of 12-EDO. The fifth is defined as the nearest approximation to 3/2. There is a little leeway to this in certain EDOs like 18 which have two possible fifths with nearly equal accuracy.
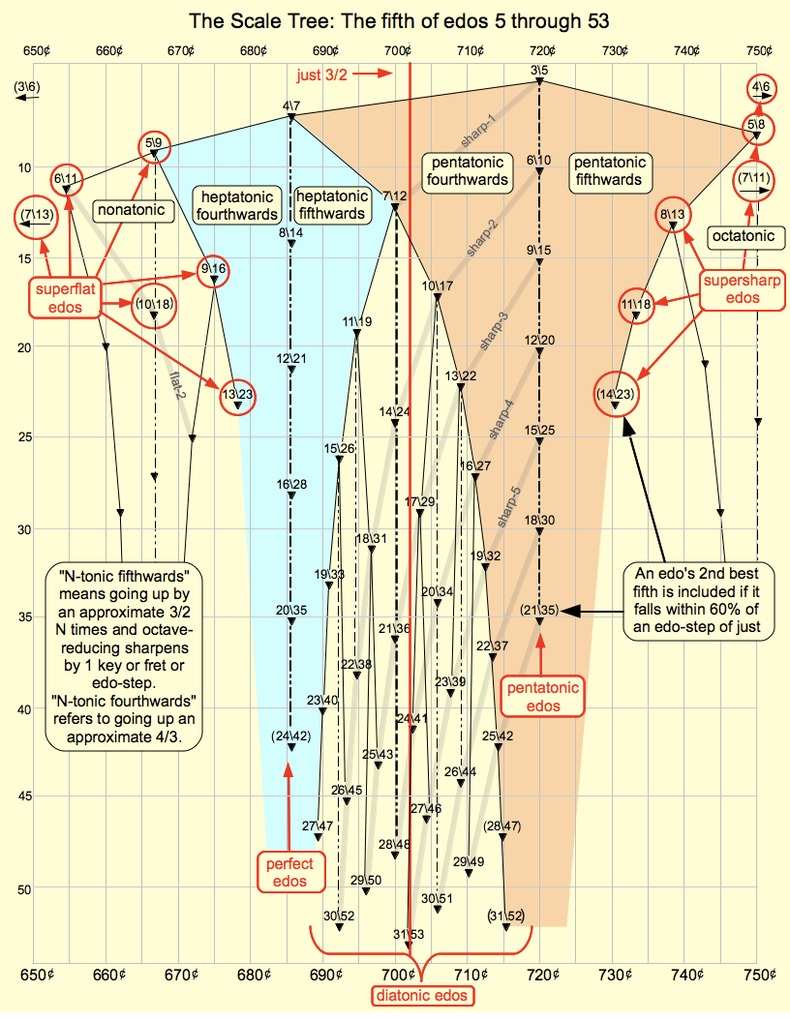
The above diagram is actually a section of the Stern-Brocot tree. The tree usually has ratios, not octave fractions (i.e. 4/7, not 4\7 as above). Also it's usually arranged vertically with nodes of the same "generation" occurring at the same height. For example, 5\9 and 7\12 are both children of 4\7, and would usually be level with each other. Here the nodes are arranged vertically by denominator, i.e., the EDO itself. This version of the Stern-Brocot tree is the scale tree. The colored regions of the tree are kites. The heptatonic kite is blue and the pentatonic kite is orange. Every kite has a head (4\7 for the blue kite), a central spine (8\14, 12\21, etc.), a fifthward side on the right (7\12, 11\19, etc.) and a fourthward side on the left (5\9, 9\16, etc.). Every node on a spine is a spinal node. Every non-spinal node is part of three kites. It's the head of one kite and on the side of two others.
Every EDO with a node on the head or either side of the heptatonic kite (7, 9, 12, 16, 19, 23, etc.) can be notated heptatonically without using ups and downs. All others require ups and downs. Likewise the pentatonic kite, minus the spine, contains the only EDOs that can be notated pentatonically without ups and downs.
The diagram only shows part of the full Stern-Brocot tree, which extends sideways from 0¢ (0\1) to 1200¢ (1\1). The full tree contains four pentatonic kites and six heptatonic kites. The blue kite is the 4\7 kite; the others are the 1\7, 2\7 3\7, 5\7 and 6\7 kites. The 3\7 kite is the mirror image of the 4\7 kite, 5\7 mirrors 2\7, and 6\7 mirrors 1\7. The 4\7 kite contains EDOs best notated by heptatonic notation generated by the fifth (i.e., to sharpen or augment means to add seven fifths, octave-reduced). The octave inverse of the generator is also a generator, thus fourth-generated is equivalent to fifth-generated, and the 3\7 kite contains the exact same EDOs as the 4\7 kite. The 2\7 kite is for notation generated by thirds, and the 1\7 kite is for notation generated by seconds.
Every EDO larger than 7edo will appear on only one of these three mirror-pairs of kites. The only exception is perfect EDOs, which appear on the spine of every heptatonic kite. This means that every non-perfect EDO above 7edo has a "natural" (not requiring ups and downs) notation, generated by either the 2nd, the 3rd, or the 5th. For now we'll assume that the fifth is the notation's generator. More on alternate generators later.
As we've seen, 19-EDO doesn't require ups and downs. Let the keyspan of the octave in an EDO be K1 and the keyspan of the fifth be K2. For example, in 12-EDO, K1 = 12 and K2 = 7. The stepspan is one less than the degree. For our usual heptatonic framework, the stepspan of the octave S1 is 7 and the stepspan of the fifth S2 is 4. In order for ups and downs to be unnecessary, S1 * K2 - S2 * K1 = +/-1. Examples of EDOs that don't need ups and downs are 5, 12, 19, 26, 33, 40, etc. (every 7th EDO). There are 4 other such EDOs, 7, 9, 16 and 23. All other EDOs need ups and downs.
22-EDO is a sharp-3 edo because a sharp equals 3 ups. 17-EDO is sharp-2.
The mid symbol "~" means "exactly midway between major and minor", hence neutral. In other words, mid is a quality like major or perfect. This only applies to EDOs in which the sharpness is an even number. For example, every seventh EDO (10edo, 17edo, 24edo, 31edo, etc.) is a sharp-2 EDO, upminor equals downmajor, and "mid" replaces both terms. 20edo, 27edo, 34edo, 41edo, etc., are sharp-4 EDOs, and mid replaces both double-upminor and double-downmajor. 11-edo and 18b-edo are flat-2 EDOs, and mid replaces upmajor and downminor.
There are three special cases to be addressed. The first special case is when the edo's fifth equals 4\7, as in 7edo, 14edo, 21edo, 28edo, and 35edo. (42edo, 49edo, etc. have a fifth wider than 4\7.) These five edos are sharp-0 edos, and all intervals are perfect. The scale that is produced by a chain of fifths is exactly the same scale as produced by a chain of 2nds, 3rds, 4ths, etc. Since any of these intervals is a potential generator, and since the generator is perfect by definition, they must all be perfect. There are no major or minor intervals.
The chain of fifths in perfect EDOs (3/2 maps to 4\7) is a circle of 7 notes:
P2 - P6 - P3 - P7 - P4 - P1 - P5 - P2 - P6 - P3 - P7 etc.
F - C - G - D - A - E - B - F - C - G - D - A - E - B etc.
21edo: P1 - ^P1 - vP2 - P2 - ^P2 - vP3 - P3 - ^P3 - vP4 - P4 - ^P4 - vP5 - P5 - ^P5 - vP6 - P6 - ^P6 - vP7 - P7 - ^P7 - vP8 - P8
Because everything is perfect, the quality can be omitted:
21edo: 1 - ^1 - v2 - 2 - ^2 - v3 - 3 - ^3 - v4 - 4 - ^4 - v5 - 5 - ^5 - v6 - 6 - ^6 - v7 - 7 - ^7 - v8 - 8
21edo: C - C^ - Dv - D - D^ - Ev - E - E^ - Fv - F - F^ - Gv - G - G^ - Av - A - A^ - Bv - B - B^ - Cv - C
Just as ups and downs aren't needed in 19edo, sharps and flats aren't needed in 21edo. The sharp symbol actually indicates raising by zero EDOsteps, and F = F#. One could simply redefine the sharp and flat symbols to mean up and down in perfect EDOs, perhaps to make one's notation software easier to use. But this would be confusing, because the upfifth B - F# would look like a perfect fifth.
The second special case is when the edo's fifth is wider than 3\5, as in 8edo, 13edo and 18edo. Heptatonic fifth-based notation is possible in these cases. The minor 2nd, which is the sum of five 4ths minus two 8ves, becomes a descending interval. Thus the major 3rd is wider than the perfect 4th, etc. 13edo and 18edo can be notated by using the 2nd best fifth.
The third special case is when the edo's 5th is narrower than 4\7, as in 16edo. There are two approaches. One preserves the harmonic (chain-of-fifths) meaning of sharp/flat, major/minor and aug/dim, and the other preserves the melodic meaning.
In the first approach, major is still fifthwards, which makes it narrower than minor. Aug is narrower than dim. This makes interval arithmetic and chord names unaffected. M2 + M2 is still M3, and a C minor chord is still C Eb G. Sharp is flatter than natural. Up is still ascending in pitch. If someone's singing above pitch, instead of saying "you're singing sharp", you would say "you're singing up".
In the 2nd approach, major is still wider than minor, so major is not fifthwards but fourthwards. Sharp is still sharper than natural. The chain of fifths: M2 - M6 - M3 - M7 - P4 - P1 - P5 - m2 - m6 - m3 - m7 - d4 - d1 etc.
F# - C# - G# - D# - A# - E# - B# - F - C - G - D - A - E - B - Fb - Cb - Gb - Db - Ab - Eb - Bb - Fbb etc.
16edo: P1 - A1/d2 - m2 - M2 - m3 - M3 - A3/d4 - P4 - A4/d5 - P5 - A5/d6 - m6 - M6 - m7 - M7 - A7/d8 - P8
16edo: C - C#/Db - D - D#/Eb - E - E# - Fb - F - F#/Gb - G - G#/Ab - A - A#/Bb - B - B# - Cb - C
Interval arithmetic is done using a simple trick: first reverse everything, then perform normal arithmetic, then reverse everything again. Reversing means exchanging major for minor, aug for dim, and sharp for flat. Perfect and natural are unaffected. Examples:
| initial question | reverse everything | do the math | reverse again |
| M2 + M2 | m2 + m2 | dim3 | aug3 |
| D to F# | D to Fb | dim3 | aug3 |
| D to F | D to F | m3 | M3 |
| Eb + m3 | E# + M3 | G## | Gbb |
| Eb + P5 | E# + P5 | B# | Bb |
| A minor chord | A major | A C# E | A Cb E |
| Eb major chord | E# minor | E# G# B# | Eb Gb Db |
| Gm7 = G + m3 + P5 + m7 | G + M3 + P5 + M7 | G B D F# | G B D Fb |
| Ab7aug = Ab + M3 + A5 + m7 | A# + m3 + d5 + M7 | A# C# E G## | Ab Cb E Gbb |
| what chord is D F A#? | D F Ab | D + m3 + d5 | D + M3 + A5 = Daug |
| what chord is C E Gb Bb? | C E G# B# | C + M3 + A5 + A7 | C + m3 + d5 + d7 = Cdim7 |
| C major scale = C + M2 + M3
+ P4 + P5 + M6 + M7 + P8 |
C + m2 + m3 + P4
+ P5 + m6 + m7 + P8 |
C Db Eb F
G Ab Bb C |
C D# E# F
G A# B# C |
| C minor scale = C + M2 + m3
+ P4 + P5 + m6 + m7 + P8 |
C + m2 + M3 + P4
+ P5 + M6 + M7 + P8 |
C Db E F
G A B C |
C D# E F
G A B C |
| what scale is A B# Cb D
E F Gb A? |
A Bb C# D
E F G# A |
A + m2 + M3 + P4
+ P5 + m6 + M7 |
A + M2 + m3 + P4
+ P5 + M6 + m7 = A dorian |
Both approaches have their merit, but the first one will be used here.
17-EDO: (2 keys per sharp/flat)
Black and white keys: C * * D * * E F * * G * * A * * B C
Relative notation: 1 m2 ~2 M2 m3 ~3 M3 4 d5 v5 5 m6 ~6 M6 m7 ~7 M7 8 (1, 4, 5 and 8 are assumed to be perfect)
The d5 could instead be an A4: P4 ^P4 A4 P5 or P4 vA4 A4 P5
Many other variations are possible, much freedom of spelling.
In C, with downmajors: C Db Dv D Eb Ev E F Gb Gv G Ab Av A Bb Bv B C
In B, with upminors: B C C^ C# D D^ D# E F F^ F# G G^ G# A A^ A# B
One can't associate ups and downs with yellow and green because of the poor approximation of the 5-limit. However major = red or fifthward white, minor = blue or fourthward white, and downmajor = upminor = jade or amber.
24-EDO: (2 keys per sharp/flat)
black and white keys: C * * * D * * * E * F * * * G * * * A * * * B * C
Relative notation: P1 ^P1/vm2 m2 ~2 M2 ^M2/vm3 m3 ~3 M3 ^M3/vP4 P4 ^P4 A4/d5 vP5 P5 etc.
In C: C C^/Dbv C#/Db Dv D D^/Ebv D#/Eb Ev E E^/Fv F F^ F#/Gb Gv G etc.
JI associations: Major = yellow or fifthward white, minor = green or fourthward white, upmajor = red, downminor = blue, downmajor = upminor = jade or amber.
24-EDO is an example of a multi-ring EDO. An EDO is multi-ring if the keyspan of the generator (usually the fifth) isn't coprime with the keyspan of the octave, and single-ring or 1-ring if it is. 24-EDO has a fifth of 14 steps, and is 2-ring because there are 2 unconnected circles of 12 fifths. They are notated as the mid one and the up one:
Eb - Bb - F - C - G - D - A - E - B - F# - C# - G#/Ab - Eb
Eb^ - Bb^ - F^ - C^ - G^ - D^ - A^ - E^ - B^ - F#^ - C#^ - G#^/Ab^ - Eb^
Just as G# could alternatively be written as Ab, all the up notes could alternatively be written as down notes.
In 1-ring EDOs, we can require that the tonic be a mid note. For example in 22-EDO, rather than using C#v as a tonic, we could use B#. But multi-ring EDOs force the use of tonics that are not a mid note. For example, the key of C^ runs:
C^ Db Db^ D D^ Eb Eb^ E E^ F F^ F^^ Gb^ G G^ etc.
31-EDO: (2 keys per sharp/flat)
Black and white keys: C * * * * D * * * * E * * F * * * * G * * * * A * * * * B * * C
relative notation: P1 ^P1 vm2 m2 ~2 M2 ^M2 vm3 m3 ~3 M3 ^M3 vP4 P4 ^P4 A4 d5 ^d5 P5 etc.
alternate spellings: A1=vm2, ^m2=vM2, ^M3=vP4, ^P4=vA4, etc.
In C: C C^ Dbv Db Db^ D D^ Ebv Eb Eb^ E E^ Fv F F^ F# Gb Gb^ G etc.
JI associations: Perfect = white, major = yellow or fifthward white, minor = green or fourthward white, downminor = blue, upmajor = red, downmajor = upminor = jade or amber (same as 24-EDO).
41-EDO: (4 keys per sharp/flat)
Black and white keys: C * * * * * * D * * * * * * E * * F * * * * * * G * * * * * * A * * * * * * B * * C
P1 ^P1 vm2 m2 ^m2 ~2 vM2 M2 ^M2 vm3 m3 ^m3 ~3 vM3 M3 ^M3 vP4 P4 ^P4 ^^P4 d5 ^d5 vvP5 vP5 P5 etc.
In C: C C^ Dbv Db Db^ D D^ Ebv Eb Eb^ E E^ Fv F F^ F# Gb Gb^ G etc.
JI associations: Perfect = white, major = fifthward white, minor = fourthward white, downmajor = yellow, upminor = green, downminor = blue, upmajor = red, double-downmajor = double-upminor = jade or amber.
22edo Chord Names
Ups and downs allow us to name any chord easily. The quality of an interval (major, minor, perfect, etc.) is defined by its position on the chain of 5ths. Perfect is 0-1 steps away, major/minor are 2-5 steps away, aug/dim are 6-12 steps away, etc.
Chord names are based entirely on the ups/downs interval names, not on JI ratios. This avoids identifying one EDOstep with multiple ratios, as happens in 22edo when 0-7-18 implies 4:5:7 but 0-9-18 implies 9:12:16. 18\22 is neither 7/4 nor 16/9, it's 18\22!
Let's review the 22edo interval names:
0\22 = P1
1\22 = m2
2\22 = ^m2
3\22 = vM2
4\22 = M2
5\22 = m3
6\22 = ^m3
7\22 = vM3
8\22 = M3
9\22 = P4
10\22 = ^P4, d5
11\22 = vA4, ^d5
12\22 = A4, vP5
13\22 = P5
14\22 = m6
15\22 = ^m6 (d7 in a dim7 chord)
16\22 = vM6
17\22 = M6
18\22 = m7
19\22 = ^m7
20\22 = vM7
21\22 = M7
22\22 = P8
These are pronounced "downmajor second", "upminor third", etc. For 4ths and 5ths, "perfect" is implied and can be omitted: ^P4 = "up-fourth" and vP5 = "down-fifth". In larger edos there may be "down-octave", "up-unison", etc.
There are some alternate names. However double-ups and double-downs are to be avoided in 22edo. Thus 7\22 would never be written ^^m3. In larger edos, double-ups and double-downs would be necessary.
0-8-13 in C has C E & G, and is written C and pronounced "C" or "C major".
0-7-13 = C Ev G is written C.v, spoken as "C downmajor" or "C dot down".
The period is needed because Cv, spoken as "C down", is either a note, or a major chord Cv Ev Gv.
0-6-13 = C Eb^ G = C.^m, "C upminor"
0-5-13 = C Eb G = Cm, "C minor"
The period isn't needed in the last chord name because there's no ups or downs immediately after the note name.
0-8-13-18 = C E G Bb = C7, "C seven", a standard C7 chord with a M3 and a m7.
0-7-13-18 = C Ev G Bb = C7(v3), "C seven, down third". The altered note or notes are in parentheses.
0-8-13-21 = C E G B = CM7, "C major seven".
0-7-13-20 = C Ev G Bv = C.vM7, "C downmajor seven". The down symbol affects both the 3rd and the 7th.
Often the root of a chord will not be a mid note. The root in the next two examples is Cv.
0-8-13-21 = Cv Ev Gv Bv = Cv.M7, "C down, major seven"
To distinguish between C.vM7 and Cv.M7, one has to pronounce the period with a small pause.
0-7-13-20 = Cv Evv Gv Bvv = Cv.vM7, "C down, downmajor seven".
Sus chords: as in conventional notation, "sus" means the 3rd is replaced by the named note, a 2nd or 4th. "Sus4" implies a perfect 4th, and other 4ths are specified explicitly as sus^4 for an up-fourth, etc. Certain larger edos might have susv4, susvv4, etc. "Sus2" implies a major 2nd. In most edos, this M2 is always a perfect 4th below the perfect 5th, implying an approximate 8:9:12 chord. See the superflat EDOs below for an exception.
Aug-3 and dim-3 chords: many of the larger EDOs have an aug 3rd distinct from the perfect 4th, and a dim 3rd distinct from the major 2nd. An A3,P5 chord is C(A3) = "C aug-three" (not "C aug", because that refers to the conventional aug chord M3,A5). Likewise d3,P5 is C(d3) = "C dim-three", and m3,d5 is Cdim.
0-3-13 = C Dv G = C(v2)
0-4-13 = C D G = C2
0-5-13 = C Eb G = Cm
0-6-13 = C Eb^ G = C.^m
0-7-13 = C Ev G = C.v
0-8-13 = C E G = C
0-9-13 = C F G = C4
0-10-13 = C F^ G = C(^4)
0-5-10 = C Eb Gb = Cdim
0-5-11 = C Eb Gb^ = Cdim(^5)
0-5-12 = C Eb Gv = Cm(v5)
0-5-10-15 = C Eb Gb Bbb = Cdim7
0-5-11-14 = C Eb Gb^ Bbbv = Cdim7(^5,v7)
0-6-11-15 = C Eb^ Gb^ Bbb = Cdim7(^3,^5)
0-6-11-16 = C Eb^ Gb Bbb^ = C.^dim7 (the up symbol applies to both the 3rd and the 7th)
0-5-13-17 = C Eb G A = Cm6
Sometimes doubled ups/downs are unavoidable:
0-6-12-15 = C Eb^ Gv Avv = C.^m(v5)vv6, or C Eb^ Gb^^ Bbb = Cdim7(^3,^^5)
0-8-13-17 = C E G A = C6
0-8-13-16 = C E G Av = C(v6)
0-7-13-17 = C Ev G A = C6(v3)
0-7-13-16 = C Ev G Av = C.v6 (the down symbol applies to both the 3rd and the 6th)
0-5-13-18 = C Eb G Bb = Cm7
0-6-13-19 = C Eb^ G Bb^ = C.^m7
0-7-13-20 = C Ev G Bv = C.vM7
0-8-13-21 = C E G B = CM7
0-5-13-16 = C Eb G Av = Cm,v6
0-8-13-19 = C E G Bb^ = C,^7
0-7-13-18-26 = C Ev G Bb D = C9(v3)
0-7-13-18-26-32 = C Ev G Bb D F^ = C9(v3)^11
You can write out chord progressions using ups/downs notation to name the roots. Here's the first 4 chords of Paul Erlich's 22edo composition "Tibia":
G.vM7no5 = "G dot down major seven, no five"
Eb^.v,9 = "E-upflat dot down, add nine"
C7(4) = "C-seven sus-four"
A7(v3) = "A-seven down-three"
Here are all possible 22edo chord roots in relative notation:
I
^I or bII
v#I or ^bII
- I or vII
II
^II or bIII
v#II or ^bIII
- II or vIII
III
IV
^IV or bV
v#IV or ^bV
- IV or vV
V
^V or bVI
v#V or ^bVI
- V or vVI
VI
^VI or bVII
v#VI or ^bVII
- VI or vVII
VII or vI
These are pronounced "down-two", "up-flat-three", "down-sharp-four", etc. Periods are used as before, for consistency, although they are not always needed. Thus 1 - M3 - 5 - vm7 = I,v7 = "one down-seven", 1 - vM3 - 5 - vm7 = I.v7 = "one dot down seven", and v1 - vM3 - v5 - vm7 = vI7 = "down-one seven". Here's the "Tibia" chords again:
I.vM7no5 = "one dot down major seven, no five"
^bVI.v,9 = "upflat-six dot down, add nine"
IV7(4) = "four-seven sus-four"
II7(v3) = "two-seven down-three"
Chord names in other EDOs
In chord names, the mid symbol "~" means "exactly midway between major and minor", hence neutral. This only applies to even-sharpness edos. In sharp-2 edos (10, 17, 24, etc.), upminor equals downmajor, and "mid" replaces both terms. In sharp-4 edos (20, 27, 34, etc.), mid replaces both double-upminor and double-downmajor. In 11-edo and 18b-edo, mid replaces both upmajor and downminor.
Alterations are enclosed in parentheses, additions never are.
In perfect EDOs (7, 14, 21, 28 and 35), every interval is perfect, and there is no major or minor. In the following list of chord names, omit major, minor, dim and aug. Substitute up for upmajor and upminor, and down for downmajor and downminor. The C-E-G chord is called "C perfect" or simply "C". The D-F-A chord is "D perfect" or "D".
A period in a chord name is pronounced as "dot". For example, C.v = C Ev G is "C dot down", because "C down" means Cv major = Cv Ev Gv. If there are any words after the up/down, a slight pause suffices, e.g. C.vm = "C downminor" and Cv.m = "C-down minor". This is analogous to saying "A-flat nine" for Ab C Eb Gb Bb vs. "A flat-nine" for A C# E G Bb. Even if the period doesn't need to be pronounced, it's always acceptable to do so. However C.v7 must be "C dot down-seven" because "C down-seven" is C,v7 = C E G Bbv.
Applying "dot up" or "dot down" to a chord raises or lowers the 3rd, and also the 6th or the 7th or the 11th, if present. Thus "C dot down nine" is the usual C9 chord with the 3rd and 7th lowered: C.v9 = C Ev G Bbv D. A "dot mid" chord has a neutral 3rd and a neutral 6th/7th, and a half-augmented 11th. The rationale for this rule is that a chord often has a note a perfect fourth or fifth above the 3rd. Furthermore, in many EDOs, upfifths, downfifths, upfourths and downfourths will all be quite dissonant and rarely used in chords. Thus if the 3rd is upped or downed, the 6th or 7th likely would be too. However the 9th likely wouldn't, because that would create an upfifth or a downfifth with the 5th. If the 7th is upped or downed, the 11th would be too.
To find a chord's name, determine its component notes, then use the following tables. These tables aren't exhaustive, but they do provide enough examples to extrapolate from.
Various triads:
C D G = C2 = "C two"
C D^ G = C(^2) = "C up-two" (not "C-up two", which would be C^.2 = C^ D^ G^)
C D^^ G = C(^^2) = "C double-up-two"
C Eb G = Cm = "C minor" (in perfect EDOs, C = "C" or "C perfect")
C Ebv G = C.vm = "C downminor" (in perfect EDOs, C.v = "C dot down") (not "C-down minor" = Cv.m = Cv Ebv Gv)
C Ebvv G = C.vvm = "C double-downminor" (not "C-double-down minor" = Cvv.m = Cvv Ebvv Gvv)
C Eb^ G = C.^m = "C upminor" (in EDOs 10, 17, 24, 31, etc., C~ = "C mid")
C Eb^^ G = C.^^m = "C double-upminor" (in EDOs 20, 27, 34, 41, etc., C~ = "C mid")
C E G = C = "C" or "C major" (in perfect EDOs, "C" or "C perfect")
C Ev G = C.v = "C downmajor" or "C dot down" (in EDOs 10, 17, 24, 31, etc., C~ = "C mid")
C Evv G = C.vv = "C double-downmajor" or "C dot double-down" (in EDOs 20, 27, 34, 41, etc., C~ = "C mid")
C E^ G = C.^ = "C upmajor" or "C dot up" (not "C up", which would be C^ major = C^ E^ G^)
C E^^ G = C.^^ = "C double-upmajor" or "C dot double-up"
C F G = C4 = "C four"
C Fv G = C(v4) = "C down-four"
C Fvv G = C(vv4) = "C double-down-four"
C D# G = C(#2) or C(A2) = "C sharp-two" or "C aug-two"
C Ebb G = C(d3) or C(bb3) = "C dim-three" or "C double-flat-three"
C E# G = C(#3) or C(A3) = "C sharp-three" or "C aug-three"
C Fb G = C(b4) or C(d4) = "C flat-four" or "C dim-four"
Altered fifths:
C Eb Gb = Cdim = "C dim" (in perfect EDOs, C = "C" or "C perfect")
C Eb Gbv = Cdim(v5) = "C dim down-five"
C Eb Gb^ = Cdim(^5) = "C dim up-five"
C Eb^ Gb = C.^dim = "C up-dim" (in certain EDOs, C~dim = "C mid-dim")
C Eb^ Gb^ = C.^dim(^5) = "C up-dim up-five" (in certain EDOs, C~(^b5) = "C mid upflat-five")
C Eb Gv = Cm(v5) = "C minor down-five"
C Ebv Gv = C.vm(v5) = "C downminor down-five"
C E Gv = C(v5) = "C down-five" (not "C-down five", which would be a Cv power chord Cv.5 = Cv Gv)
C E G^ = C(^5) = "C up-five"
C E^ G^ = C.^(^5) = "C dot up up-five" or "C upmajor up-five"
C Ev Gv = C.v(v5) = "C dot down down-five" or "C downmajor down-five" (in certain EDOs, C~(v5) = "C mid down-five")
C E G# is Caug = "C aug" (in perfect EDOs, C = "C" or "C perfect")
C E G#v = Caug(v5) = "C aug down-five"
C E G#^ = Caug(^5) = "C aug up-five"
C E^ G# is C.^aug = "C up-aug"
C E^ G#^ = C.^aug(^5) = "C up-aug up-five"
C D# Gb = C(#2,b5) = "C sharp-two, flat-five"
C Ebb Gb = Cdim(d3) or Cdim(bb3) = "C dim dim-three" or "C dim double-flat-three"
C Eb G# is Cmin(#5) = "C minor sharp-five"
C E# G# is Caug(#3) = "C aug sharp-three"
C Fb G# is C(b4,#5) = "C flat-four sharp-five"
Seventh chords:
C E G Bb = C7 = "C seven"
C Ev G Bb = C7(v3) = "C seven down-three" (in certain EDOs, C7(~3) = "C seven mid-three")
(here "down-three" means downmajor 3rd, not downminor 3rd, because "C7" indicates a major 3rd)
C E G Bbv = C,v7 = "C down-seven" (not "C-down seven", which would be Cv.7 = Cv Ev Gv Bbv)
C Ev G Bbv = C.v7 = "C dot down seven" (in certain EDOs, C~,v7 = "C mid down-seven")
C E Gv Bb = C7(v5) = "C seven down-five"
C Ev Gv Bb = C7(v3,v5) = "C seven down-three down-five"
C Ev Gv Bbv = C.v7(v5) = "C dot down seven, down-five"
C Ev G Bbvv = C.v,vv7 = "C dot down, double-down seven"
C E G Bb^ = C,^7 = "C up-seven" (in certain EDOs, C,~7 = "C mid-seven")
C Ev G Bb^ = C.v,^7 = "C dot down up-seven" (in certain EDOs, C.~7 = "C dot mid-seven")
C Eb G Bb = Cm7 = "C minor seven" (in perfect EDOs, C7 = "C seven")
C Eb^ G Bb = Cm7(^3) = "C minor seven up-three" (in certain EDOs, C7(~3) = "C seven mid-three")
C Eb G Bb^ = Cm,^7 = "C minor up-seven" (in certain EDOs, Cm,~7 = "C minor mid-seven")
C Eb^ G Bb^ = C.^m7 = "C dot up minor-seven" (in certain EDOs, C.~7 = "C dot mid seven")
C E G B = CM7 = "C major seven" (in perfect EDOs, C7 = "C seven")
C Ev G B = CM7(v3) = "C major seven down-three"
C E G Bv = C,vM7 = "C downmajor-seven"
C Ev G Bv = C.vM7 = "C dot down major-seven"
C Eb Gb Bbb = Cdim7 = "C dim seven" (in perfect EDOs, C7 = "C seven")
C Eb^ Gb Bbb = Cdim7(^3) = "C dim seven up-three" (in certain EDOs, Cdim7(~3) = "C dim seven mid-three")
C Eb Gb^ Bbb = Cdim7(v5) = "C dim seven up-five"
C Eb Gb Bbb^ = Cdim,^d7 = "C dim updim-seven"
C Eb^ Gb Bbb^ = C.^dim7 = "C dot up dim-seven"
C Eb^ Gb^ Bbb^ = C.^dim7(^5) = "C dot up dim-seven up-five"
C Eb Gb Bb = Cm7(b5) = "C minor seven flat-five" or "C half-dim" (in perfect EDOs, C7 = "C seven")
C Eb^ Gb Bb = Cm7(b5,^3) = "C minor seven flat-five up-three" or "C half-dim up-three"
C Eb Gb^ Bb = Cm7(^b5) = "C minor seven upflat-five" or "C half-dim up-five"
C Eb Gb Bb^ = Cdim,^7 = "C dim up-seven" or "C half-dim up-seven"
C Eb^ Gb^ Bb = Cm7(^b5,^3) = "C minor seven up-three upflat-five" or "C half-dim up-three up-five"
C Eb^ Gb Bb^ = C.^m7(b5) = "C dot up minor-seven flat-five" or "C half-dim up-three up-seven"
C Eb Gb^ Bb^ = Cdim(^5)^7 = "C dim up-five up-seven" or "C half-dim up-five up-seven"
C Eb^ Gb^ Bb^ = C.^m7(^b5) = "C dot up minor-seven upflat-five" or "C half-dim up-three up-five up-seven"
C E G Bbb = C,bb7 or C,d7 = "C double-flat-seven" or "C major dim-seven" (not "C dim-seven" = Cdim7)
C E G B# is C,#7 or C,A7 = "C sharp-seven" or "C major aug-seven" (not "C aug-seven" = Caug7)
C E G Cb = C,b8 or C,d8 = "C flat-eight" or "C dim-eight"
Sixth chords:
C E G A = C6 = "C six"
C Ev G A = C6(v3) = "C six down-three" (in certain EDOs, C6(~3) = "C six mid-three")
C E G Av = C,v6 = "C down-six" (in certain EDOs, C,~6 = "C mid-six")
C Ev G Av = C.v6 = "C dot down six" (in certain EDOs, C.~6 = "C dot mid six")
C Eb G A = Cm6 = "C minor six" (in perfect EDOs, C6 = "C six")
C Eb^ G A = Cm6(^3) = "C minor six up-three" (in certain EDOs, C6(~3) = "C six mid three")
C Eb G Av = Cm,v6 = "C minor down-six" (in certain EDOs, Cm,~6 = "C minor mid-six")
C Eb^ G A^ = C.^m6 = "C dot up minor-six"
C Eb^ G A = Cm6(^3) = "C minor six up-three" (in certain EDOs, C6(~3) = "C six mid-three")
C E G Ab = C,b6 = "C flat-six" (not "C minor-six" because that sounds like "C minor six" = Cm6)
C E G A# is C,#6 = "C sharp-six"
Ninth chords:
C D E G = C,9 = "C add nine"
C D Ev G = C.v,9 = "C dot down add nine" or "C downmajor add nine"
C D^ E G = C,^9 = "C add up-nine"
C D^ E^ G = C.^,^9 = "C dot up add up-nine" or "C upmajor add up-nine"
C D E G Bb = C9 = "C nine"
C D Ev G Bb = C9(v3) = "C nine down-three" (in certain EDOs, C9(~3) = "C nine mid-three")
C D E G Bb^ = C9(^7) = "C nine up-seven" (in certain EDOs, C9(~7) = "C nine mid-seven")
C Dv E G Bb = C7(v9) = "C seven down-nine" or C9(v9) = "C nine down-nine"
C D Ev G Bbv = C.v9 = "C dot down nine"
C Dv Ev G Bb = C7(v3)v9 = "C seven down-three down-nine"
C Dv E G Bbv = C,v7,v9 = "C down-seven down-nine"
C Dv Ev G Bbv = C.v7,v9 = "C dot down seven down-nine"
C Dv Ev Gv Bbv = C.v7(v5)v9 = "C dot down-seven down-five down-nine"
C D E G B = CM9 = "C major nine" (in perfect EDOs, C9 = "C nine")
C D Ev G B = CM9(v3) = "C major nine down-three" (in certain EDOs, CM9(~3) = "C major nine mid-three")
C D E G Bv = CM9(v7) = "C major nine down-seven" (in certain EDOs, CM9(~7) = "C major nine mid-seven")
C D Ev G Bv = C.vM9 = "C dot down major-nine" (in certain EDOs, C.~M9 = "C dot mid major nine")
C D Eb G Bb = Cm9 = "C minor nine" (in perfect EDOs, C9 = "C nine")
C D Eb^ G Bb = Cm9(^3) = "C minor nine up-three" (in certain EDOs, C9(~3) = "C nine mid-three")
C D Eb G Bb^ = Cm9(^7) = "C minor nine up-seven" (in certain EDOs, Cm9(~7) = "C minor nine mid-seven")
C D Eb^ G Bb^ = C.^m9 = "C dot up minor-nine" (in certain EDOs, C.~M9 = "C dot mid major nine")
C Db E G Bb = C7,b9 = "C seven flat-nine" (in perfect EDOs, C9 = "C nine")
C Db Ev G Bb = C7,b9(v3) = "C seven flat-nine down-three"
C Db E G Bbv = C,v7,b9 = "C seven flat-nine down-seven"
C Dbv E G Bb = C7,vb9 = "C seven downflat-nine"
C Db Ev G Bbv = C.v7,b9 = "C dot down seven flat-nine"
C Dbv Ev G Bb = C7(v3)vb9 = "C seven down-three downflat-nine"
C Dbv E G Bbv = C,v7,vb9 = "C down-seven downflat-nine"
C Dbv Ev G Bbv = C.v7,vb9 = "C dot down seven downflat-nine"
Example EDOs:
14edo: D * E * F * G * A * B * C * D, zero keys per #/b.
(the chain of fifths is always centered on D, for symmetry)
chord components: P1 vP2 P2 vP3 P3, etc.
Because every interval is perfect, the quality can be omitted
chord components: 1 v2 2 v3 3 ^3/v4 4 ^4/v5 5 v6 6 ^6/v7 7 ^7
chord roots: I ^I/vII II ^II/vIII III vIII/vIV IV ^IV/vV V ^V/vVI VI ^VI/vVII VII ^VII/vI
0-3-8 = D Fv A = D.v = "D dot down" or "D downperfect"
0-4-8 = D F A = D = "D" or "D perfect"
0-5-8 = D F^ A = D.^ = "D dot up"
0-3-7 = D Fv Av = D.v(v5) = "D dot down, down-five"
0-4-7 = D F Av = D(v5) = "D down-five"
0-4-9 = D F A^ = D(^5) = "D up-five"
0-5-9 = D F^ A^ = D.^(^5) = "D dot up, up-five"
0-4-8-11 = D F A Cv = D,v7 = "D down-seven", or D F A B^ = D,^6 = "D up-six"
0-3-8-11 = D Fv A Cv = D.v7 = "D dot down seven"
0-5-8-11 = D F^ A B^ = D.^6 = "D dot up six"
15edo: 3 keys per #/b, so ups and downs are needed.
keyboard/fretboard: D * * E/F * * G * * A * * B/C * * D
chord components: P1 ^m2 vM2 M2/m3 ^m3 vM3 M3/P4 ^P4 vP5 P5 ^m6 vM6 M6/m7 ^m7 vM7
chord roots: I ^bII vII II/bIII ^bIII vIII III/IV ^IV vV V ^bVI vVI VI/bVII ^bVII vVII
0-3-9 = D F A = Dm = "D minor" (or possibly D E A = Dsus2)
0-4-9 = D F^ A = D.^m = "D upminor"
0-5-9 = D F#v A = D.v = "D dot down" or "D downmajor"
0-6-9 = D F# A = D = "D" or "D major" (or possibly D G A = Dsus4)
0-3-9-12 = D F A C = Dm7 = "D minor seven", or D F A B = Dm6 = "D minor six"
0-4-9-12 = D F^ A C = Dm7(^3) = "D minor seven up-three", or D F^ A B = Dm6(^3) = "D minor six up-three"
0-5-9-12 = D F#v A C = D7(v3) = "D seven down-three", or D F#v A B = D6(v3) = "D six down-three"
0-6-9-12 = D F# A C = D7 = "D seven", or D F# A B = D6 = "D six"
0-5-9-14 = D F#v A C#v = D.vM7 = "D dot down major-seven"
0-4-9-13 = D F^ A C^ = D.^m7 = "D dot up minor-seven", or D F^ A B^ = D.^m6 = "D dot up minor-six"
16edo: D * E * * F * G * A * B * * C * D, 1 key per #/b, ups and downs not needed.
if # is fourthward and raises the pitch, and major is wider than minor:
chord components: P1 d2 m2 M2 m3 M3 A3 P4 A4/d5 P5 d6 m6 M6/d7 m7 M7 A7
chord roots: I #I/bbII bII II bIII III #III/bIV IV #IV/bV V #V/bbVI bVI VI bVII VII #VII/bI
0-3-9 = D E# A = Dsus2
0-4-9 = D Fb A = Dm
0-5-9 = D F A = D (or D major)
0-5-10 = D F A# = Daug (the conventional aug chord)
0-6-9 = D F# A = D(#3) = "D sharp-three" or "D aug-three" (aug 3rd, perfect 5th)
0-7-9 = D G A = Dsus4
0-5-9-13 = D F A Cb = D7
0-4-8-12 = D Fb Ab Cbb = Ddim7 (the conventional dim tetrad)
16edo if # is fifthward and lowers the pitch, and major is narrower than minor:
chord components: P1 A2 M2 m2/A3 M3 m3 d3/A4 P4 d4/A5 P5 d5/A6 M6 m6/A7 M7 m7 d7
chord roots: I bI/#II II bII III bIII bbIII/#IV IV bIV/#V V bV/#VI VI bVI VII bVII bbVII/#I
0-3-9 = D F## A = D(#3) = "D aug-three" (or possibly D Eb A = D(b2) = "D dim-two")
0-4-9 = D F# A = D = "D" or "D major"
0-5-9 = D F A = Dm = "D minor"
0-6-9 = D Fb A = D(bb3) = "D dim-three" (or possibly D G# A = D(#4) = "D sharp-four")
0-5-10 = D F Ab = Ddim = "D dim"
0-6-10 = D Fb Ab = Ddim(bb3) = "D dim dim-three"
0-7-9 = D G A = D4 = "D four"
0-5-9-13 = D F A C# is DmM7 = "D minor-major"
0-4-8-12 = D F# A# C## is Daug,#7 = "D aug sharp-seven"
17edo: D * * E F * * G * * A * * B C * * D, 2 keys per #/b.
chord components: P1 m2 ~2 M2 m3 ~3 M3 P4 ^P4/d5 A4/vP5 P5 m6 ~6 M6 m7 ~7 M7
chord roots: I v#I/bII #I/vII II bIII vIII III IV ^IV/bV #IV/vV V #V/bVI vVI VI bVII vVII VII
0-4-10 = D F A = Dm = "D minor"
0-5-10 = D F^ A = D~ = "D mid"
0-6-10 = D F# A = D = "D" or "D major"
0-5-10-14 = D F^ A C = D7(~3) = "D seven mid-three"
0-4-10-15 = D F A C^ = Dm,~7 = "D minor mid-seven"
0-5-10-15 = D F^ A C^ = D.~7 = "D dot mid seven"
0-6-10-15 = D F# A C^ = D,~7 = "D mid-seven"
19edo: D * * E * F * * G * * A * * B * C * * D, ups and downs not needed.
chord components: P1 d2 m2 M2 d3 m3 M3 A3 P4 A4 d5 P5 A5 m6 M6 d7 m7 M7 A7
chord roots: I #I/bbII bII II #II/bbIII bIII III #III/bIV IV #IV bV V #V/bbVI bVI VI bbVII bVII VII #VII/bI
0-4-11 = D Fb A = D(d3) = "D dim-three" (dim 3rd, perfect 5th = approx. 6:7:9)
0-4-10 = D Fb Ab = Ddim(d3) = "D dim dim-three"
0-7-11 = D F## A = D(#3) = "D sharp-three" (aug 3rd, perfect 5th)
0-7-12 = D F## A# is Daug(#3) = "D aug sharp-three"
0-5-10-15 = D F Ab Cb = Ddim7 = "D dim seven"
0-6-11-15 = D F# A Cb = D(bb7) = "D double-flat-seven" (approx. 4:5:6:7)
21edo: D * * E * * F * * G * * A * * B * * C * * D, zero keys per #/b.
Because every interval is perfect, the quality can be omitted.
chord components: 1 ^1/vv2 v2 2 ^2 v3 3 ^3 v4 4 ^4 v5 5 ^5 v6 6 ^6 v7 7 ^7 ^^7/v8
chord roots: I ^I vII II ^II vIII III vIII vIV IV ^IV vV V ^V vVI VI ^VI vVII VII ^VII vI
0-4-12 = D Fvv A = D.vv = "D dot double-down", or D E^ A = Dsus^2 = "D sus up-two"
0-5-12 = D Fv A = D.v = "D dot down"
0-6-12 = D F A = D = "D" or "D perfect"
0-7-12 = D F^ A = D.^ = "D dot up" (approx. 4:5:6)
0-8-12 = D F^^ A = D.^^ = "D dot double-up", or D Gv A = D.v4 = "D down-four"
0-7-12-17 = D F^ A Cv = D.^,v7 = "D dot up down-seven" (approx. 4:5:6:7)
24edo: D * * * E * F * * * G * * * A * * * B * C * * * D, 2 keys per #/b.
chord components: P1 vm2 m2 ~2 M2 vm3 m3 ~3 M3 ^M3/vP4 P4 ^P4 A4/d5 vP5 P5 vm6 m6 ~6 M6 ^M6/vm7 m7 ~7 M7 ^M7
chord roots: I v#I/vbII #I/bII vII II vbIII bIII vIII III ^III/vIV IV ^IV #IV/bV vV V ^#V/vbVI bVI vVI VI ^VI/vbVII bVII vVII VII ^VII/vI
0-5-14 = D Fv A = D.vm = "D downminor"
0-6-14 = D F A = Dm = "D minor"
0-7-14 = D F^ A = D~ = "D mid"
0-8-14 = D F# A = D = "D" or "D major"
0-9-14 = D F#^ A = D.^ = "D dot up" or "D upmajor"
31edo: D * * * * E * * F * * * * G * * * * A etc. 2 keys per #/b.
P1 ^P1 vm2 m2 ~2 M2 ^M2 vm3 m3 ~3 M3 ^M3 vP4 P4 ^P4 A4 d5 vP5 P5 etc.
I ^I vbII bII vII II ^II vbIII bIII vIII III ^III vIV IV ^IV #IV bV vV V etc.
0-7-18 = D Fv A = D.vm = "D downminor"
0-8-18 = D F A = Dm = "D minor"
0-9-18 = D F^ A = D~ = "D mid"
0-10-18 = D F# A = D (major)
0-11-18 = D F#^ A = D.^= "D dot up" or "D upmajor"
0-12-18 = D Gv A = D(v4) = "D down-four"
41edo: C * * Db C# * * D
D * * * * * * E * * F * * * * * * G * * * * * * A * * * * * * B * * C * * * * * * D, 4 keys per sharp.
P1 ^P1 vm2 m2 ^m2 ~2 vM2 M2 ^M2 vm3 m3 ^m3 ~3 vM3 M3 ^M3 vP4 P4 ^P4 vd5 d5 A4/^d5 ^A4/vvP5 vP5 P5 etc.
I ^I vbII bII ^bII vvII vII II ^II vbIII bIII ^bIII vvIII vIII III ^III vIV IV ^IV vbV bV #IV ^#IV vV V etc.
0-10-20 = D F Ab = Ddim = "D dim"
0-10-21 = D F Ab^ = Ddim(^5) = "D dim up-five"
0-10-22 = D F Avv = Dm(vv5) = "D minor double-down five", or possibly Ddim(^^5)
0-10-23 = D F Av = Dm(v5) = "D minor down-five"
0-10-24 = D F A = Dm = "D minor"
0-11-24 = D F^ A = D.^m = "D upminor"
0-12-24 = D F^^ A = D.~ = "D mid"
0-13-24 = D F#v A = D.v = "D downmajor" or "D dot down"
0-14-24 = D F# A = D = "D" or "D major"
0-14-25 = D F# A^ = D(^5) = "D up-five"
0-14-26 = D F# A^^ = D(^^5) = "D double-up-five", or possibly Daug(vv5)
0-14-27 = D F# A#v = Daug(v5) = "D aug down-five"
0-14-28 = D F# A# is Daug = "D aug"
11edo: C# * * C D * * Db
D E F# Fv F G A B B^ Bb C D, -2 keys per sharp, upmajor = downminor = mid.
P1 M2 ~2/M3 ~3 m3 P4 P5 M6 ~6/M7 m6/~7 m7 P8
m2 m6 m3 m7 P4 P1 P5 M2 M6 M3 M7
0-1-6 = D E A = D2
0-2-6 = D F# A = D = "D major"
0-3-6 = D Fv A = D.~ = "D mid"
0-4-6 = D F A = Dm = "D minor"
0-5-6 = D G A = D4
0-2-5 = D F# Av = D(v5) = "D down-five"
0-3-5 = D Fv Av = D~(v5) = "D mid down-five"
0-3-7 = D Fv A^ = D~(^5) = "D mid up-five"
0-4-7 = D F A^ = Dm(^5) = "D minor up-five"
0-2-6-7 = D F# A B = D6
0-3-6-7 = D Fv A B = D6(~3) = "D six up-three"
0-4-6-7 = D F A B = Dm6
0-2-6-8 = D F# A C# is DM7, or D F# A B^ = D,~6 = "D mid-six"
0-3-6-8 = D F#^ A C# is DM7(^3) = "D major seven up-three", or D F#^ A B^ = D.^6 = "D dot up-six"
0-3-6-9 = D Fv A Cv = D.~7 = "D dot mid seven", or D Fv A Bb = D~,b6 = "D mid flat-six"
Cross-EDO considerations
In 22edo, the major chord is 0-8-13 = 0¢-436¢-709¢. In 19edo, it's 0-6-11 = 0¢-379¢-695¢. The two chords sound quite different, because "major 3rd" is defined only in terms of the fifth, not in terms of what JI ratios it approximates. To describe the sound of the chord, color notation can be used. 22edo major chords sound red and 19edo major chords sound yellow.
A chord quality like "major" refers not to the sound but to the function of the chord. If you want to play a I - VIm - IIm - V - I progression without pitch shifts or tonic drift, you can do that in any edo, as long as you use only major and minor chords. The notation tells you what kind of chord can be used to play that progression. In 22edo, the chord that you need sounds like a red chord.
In other words, I - VIm - IIm - V - I in just intonation implies Iy - VIg - IIg - Vy - Iy, but this implication only holds in those EDOs in which major sounds yellow. If 22edo's downmajor chord 0-7-13 = 0¢-382¢-709¢ were called "major", you wouldn't know that it doesn't work in that progression.
Another example: I7 - bVII7 - IV7 - I7. To make this work, the 7th in the I7 chord must be a minor 7th. in 22edo, that 7th sounds blue. In 19edo, it sounds green. If you want a blue 7th in 19edo, you have to use the downminor 7th, which will cause shifts or drifts in the progression.
Scale Fragments
To summarize an EDO, a scale fragment from C to D is shown, including C# and Db. Examples:
C C#/Db D (12edo)
C Db C# D (17edo)
C C# Db D (19edo)
C C# _ Db D (26edo)
C _ C# Db _ D (31edo)
The scale fragment concisely conveys the "flavor" of the EDO's notation. The C-C# interval is the augmented unison, and if the 2nd key in the fragment isn't C#, ups and downs are required. The only exception is 7edo. For most EDOs, the C-Db interval is the minor 2nd and the C-D interval is the major 2nd. For perfect EDOs, C-Db = d2 and C-D = P2. For superflat EDOs, C-Db = d2 and C-D = m2. D# is included for these EDOs because C-D# is a M2 just like E-F. For supersharp EDOs, the scale fragment isn't as helpful because you can't deduce the entire keyboard layout from it.
Every EDO contains a unique scale fragment, and every scale fragment implies a unique EDO. Furthermore, this uniqueness applies to EDOs with alternate fifths: "wide-fifth" 35edo (which uses 21\35 as a fifth) has a different scale fragment than "narrow-fifth" 35edo with 20\35. If an EDO has a fifth of keyspan F and an octave of keyspan O (i.e. it's O-EDO), the minor 2nd's keyspan is m2 = -5F + 3O, and the augmented unison's is A1 = 7F - 4O. These equations can be reversed: F = 4(m2) + 3(A1) and O = 7(m2) + 5(A1). (For perfect and superflat EDOs, substitute M2 for m2.)
| 5edo | pentatonic | C/Db | C#/D | |||||||||
| 6edo | supersharp | |||||||||||
| 7edo | perfect | C/C# | Db/D | |||||||||
| 8edo | supersharp | |||||||||||
| 9edo | superflat | C/Db | C#/D | D# | ||||||||
| 10edo | pentatonic | C/Db | * | C#/D | ||||||||
| 11edo | superflat | C | D | C# | D# | |||||||
| 12edo | regular | C | C#/Db | D | ||||||||
| 13b-edo | superflat | C | D | * | C# | D# | ||||||
| 14edo | perfect | C/C# | * | Db/D | ||||||||
| 15edo | pentatonic | C/Db | * | * | C#/D | |||||||
| 16edo | superflat | C | C#/Db | D | D# | |||||||
| 17edo | regular | C | Db | C# | D | |||||||
| 18b-edo | superflat | C/Db | * | C#/D | * | D# | ||||||
| 19edo | regular | C | C# | Db | D | |||||||
| 20edo | pentatonic | C/Db | * | * | * | C#/D | ||||||
| 21edo | perfect | C/C# | * | * | Db/D | |||||||
| 22edo | regular | C | Db | * | C# | D | ||||||
| 23edo | superflat | C | C# | Db | D | D# | ||||||
| 24edo | regular | C | * | C#/Db | * | D | ||||||
| 25edo | pentatonic | C/Db | * | * | * | * | C#/D | |||||
| 26edo | regular | C | C# | * | Db | D | ||||||
| 27edo | regular | C | Db | * | * | C# | D | |||||
| 28edo | perfect | C/C# | * | * | * | Db/D | ||||||
| 29edo | regular | C | * | Db | C# | * | D | |||||
| 30edo | pentatonic | C/Db | * | * | * | * | * | C#/D | ||||
| 31edo | regular | C | * | C# | Db | * | D | |||||
| 32edo | " | C | Db | * | * | * | C# | D | ||||
| 33edo | " | C | C# | * | * | Db | D | |||||
| 34edo | " | C | * | Db | * | C# | * | D | ||||
| 35edo | perfect | C/C# | * | * | * | * | Db/D | |||||
| 36edo | regular | C | * | * | C#/Db | * | * | D | ||||
| 37edo | " | C | Db | * | * | * | * | C# | D | |||
| 38edo | " | C | * | C# | * | Db | * | D | ||||
| 39edo | " | C | * | Db | * | * | C# | * | D | |||
| 40edo | " | C | C# | * | * | * | Db | D | ||||
| 41edo | " | C | * | * | Db | C# | * | * | D | |||
| 42edo | " | C | Db | * | * | * | * | * | C# | D | ||
| 43edo | " | C | * | * | C# | Db | * | * | D | |||
| 44ddo | " | C | * | Db | * | * | * | C# | * | D | ||
| 45edo | " | C | * | C# | * | * | Db | * | D | |||
| 46edo | " | C | * | * | Db | * | C# | * | * | D | ||
| 47edo | " | C | C# | * | * | * | * | Db | D | |||
| 48edo | " | C | * | * | * | C#/Db | * | * | * | D | ||
| 49edo | " | C | * | Db | * | * | * | * | C# | * | D | |
| 50edo | " | C | * | * | C# | * | Db | * | * | D | ||
| 51edo | " | C | * | * | Db | * | * | C# | * | * | D | |
| 52edo | " | C | * | C# | * | * | * | Db | * | D | ||
| 53edo | " | C | * | * | * | Db | C# | * | * | * | D |
Summary of EDO notation
Regular EDOs
(12, 17, 19, 22, 24, 26, 27, 29, 31-34, and all edos 36 or higher)
All regular EDOs use the usual chain of fifths: m2 - m6 - m3 - m7 - P4 - P1 - P5 - M2 - M6 - M3 - M7 etc.
Fb - Cb - Gb - Db - Ab - Eb - Bb - F - C - G - D - A - E - B - F# - C# - G# - D# - A# - E# - B# etc.
12edo: sharp/flat = 1 key, no ups and downs: C C#/Db D
C * D * E F * G * A * B C
C - C#/Db - D - D#/Eb - E - F - F#/Gb - G - G#/Ab - A - A#/Bb - B - C
P1 - A1/m2 - M2 - A2/m3 - M3 - P4 - A4/d5 - P5 - A5/m6 - M6 - A6/m7 - M7 - P8
perfect = white, major = red, yellow and fifthward white, minor = green, blue and fourthwards white
17edo: sharp = 2 keys: C Db C# D
C * * D * * E F * * G * * A * * B C
C - C^/Db - Dv/C# - D - D^/Eb - D#/Ev - Eb - E - F - F^/Gb - F#/Gv - G - G^/Ab - G#/Av - A - A^/Bb - A#/Bv - B - C
P1 - m2 - A1 - M2 - m3 - A2 - M3 - P4 - ^P4/d5 - A4/vP5 - P5 - m6 - A5 - M6 - m7 - A6 - M7 - P8
19edo: no ups and downs C C# Db D
C * * D * * E * F * * G * * A * * B * C
C - C# - Db - D - D# - Eb - E - E#/Fb - F - F# - Gb - G - G# - Ab - A - A# - Bb - B - B#/Cb - C
P1 - A1 - m2 - M2 - A2 - m3 - M3 - A3/d4 - P4 - A4 - d5 - P5 - A5 - m6 - M6 - A6 - m7 - M7 - A7/d8 - P8
perfect = white, major = yellow and fifthward white, minor = green and fourthward white, aug/dim = red/blue.
22edo: sharp = 3 keys: C Db * C# D
C * * * D * * * E F * * * G * * * A * * * B C
C - C^/Db - C#v/Db^ - C#/Dv - D - D^/Eb - D#v/Eb^ - D#/Ev - E - F - F^/Gb - F#v/Gb^ - F#/Gv - G - G^/Ab - G#v/Ab^ - G#/Av - A etc.
P1 - m2 - ^m2 - vM2 - M2 - m3 - ^m3 - vM3 - M3 - P4 - ^P4/d5 - vA4/^d5 - A4/vP5 - P5 etc.
24edo: sharp = 2 keys: C * C#/Db * D
C * * * D * * * E * F * * * G * * * A * * * B * C
C - C^/C#v - C#/Db - C#^/Dv - D - D^/Ebv - D#/Eb - D#^/Ev - E - E^/Fv - F - F^/Gbv - F#/Gb - F#^/Gv - G - G^/Abv - G#/Ab - G#^/Av - A etc.
P1 - ^P1/vA1 - A1 - ~2 - M2 - ^M2/vm3 - m3 - ~3 - M3 - ^M3/vP4 - P4 - ^P4/vd5 - A4/d5 - ^A4/vP5 - P5 etc.
etc.
Perfect EDOs
(7, 14, 21, 28 and 35)
All perfect EDOs use the same circle of 7 fifths: P4 - P1 - P5 - P2 - P6 - P3 - P7 - P4 - P1 etc.
F - C - G - D - A - E - B - F - C - G - D - A - E - B etc.
Sharp and flat are zero keys because C and C# are the same note.
7edo: C/C# Db/D
C D E F G A B C
P1 - P2 - P3 - P4 - P5 - P6 - P7 - P8
Because everything is perfect, the quality can be omitted: 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8
14edo: C/C# * Db/D
C * D * E * F * G * A * B * C
C - C^/Dv - D - D^/Ev - E - E/ Fv - F - F^/Gv - G - G^/Av - A - A^/Bv - B - B^/Cv - C
1 - ^1/v2 - 2 - ^2/v3 - 3 - ^3/v4 - 4 - ^4/v5 - 5 - ^5/v6 - 6 - ^6/v7 - 7 - ^7/v8 - 8
21edo: C/C# * * Db/D
C * * D * * E * * F * * G * * A * * B * * C
C - C^ - Dv - D - D^ - Ev - E - E^ - Fv - F - F^ - Gv - G - G^ - Av - A - A^ - Bv - B - B^ - Cv - C
1 - ^1 - v2 - 2 - ^2 - v3 - 3 - ^3 - v4 - 4 - ^4 - v5 - 5 - ^5 - v6 - 6 - ^6 - v7 - 7 - ^7 - v8 - 8
28edo: C/C# * * * Db/D
C * * * D * * * E * * * F * * * G * * * A * * * B * * * C
C - C^ - C^^/Dvv - Dv - D - D^ - D^^/Evv - Ev - E - E^ - E^^/Fvv - Fv - F - F^ - F^^/Gvv - Gv - G - G^ - G^^/Avv - Av - A etc.
1 - ^1 - ^^1/vv2 - v2 - 2 - ^2 - ^^2/vv3 - v3 - 3 - ^3 - ^^3/vv4 - v4 - 4 - ^4 - ^^4/vv5 - v5 - 5 etc.
35edo: C/C# * * * * Db/D
C * * * * D * * * * E * * * * F * * * * G * * * * A * * * * B * * * * C
C - C^ - C^^ - Dvv - Dv - D - D^ - D^^ - Evv - Ev - E - E^ - E^^ - Fvv - Fv - F - F^ - F^^ - Gvv - Gv - G - G^ - G^^ - Avv - Av - A etc.
1 - ^1 - ^^1 - vv2 - v2 - 2 - ^2 - ^^2 - vv3 - v3 - 3 - ^3 - ^^3 - vv4 - v4 - 4 - ^4 - ^^4 - vv5 - v5 - 5 etc.
Superflat EDOs
(9, 11, 13b, 16, 18b and 23)
If sharp is lower than flat, the chain of fifths is m2 - m6 - m3 - m7 - P4 - P1 - P5 - M2 - M6 - M3 - M7 etc.
Fb - Cb - Gb - Db - Ab - Eb - Bb - F - C - G - D - A - E - B - F# - C# - G# - D# - A# - E# - B# etc.
If sharp is higher than flat, the chain of fifths is M2 - M6 - M3 - M7 - P4 - P1 - P5 - m2 - m6 - m3 - m7 etc.
F# - C# - G# - D# - A# - E# - B# - F - C - G - D - A - E - B - Fb - Cb - Gb - Db - Ab - Eb - Bb etc.
Edos 11 and 13b and problematic. See "Supersharp EDOs" below for alternate notations for them.
9edo: C/D# Cb/D (# = v) with sharp lowering the pitch, and major/aug narrower than minor/dim
C D E * F G A B * C
C - D - E - Eb/F# - F - G - A - B - Bb/C# - C
P1 - M2 - m2/M3 - m3 - P4 - P5 - M6 - m6/M7 - m7 - P8
C/Db C#/D (# = ^) with sharp raising the pitch, and major/aug wider than minor/dim
C - D - E - E#/Fb - F - G - A - B - B#/Cb - C
P1 - m2 - M2/m3 - M3 - P4 - P5 - m6 - M6/m7 - M7 - P8
11edo: C D Cb Db (# = vv) with sharp lowering the pitch, and major/aug narrower than minor/dim
C D E * * F G A B * * C
C - D - E - E^/F# - Eb/Fv - F - G - A - B - B^/C# - Bb/Cv - C
P1 - M2 - ~2/M3 - m2/~3 - m3 - P4 - P5 - M6 - ~6/M7 - m6/~7 - m7 - P8
problematic because M3 is narrower than m2
C D C# D# (# = ^^) with sharp raising the pitch, and major/aug wider than minor/dim
C - D - E - E^/Fb - E#/Fv - F - G - A - B - B^/Cb - B#/Cv - C
P1 - m2 - ~2/m3 - M2/~3 - M3 - P4 - P5 - m6 - ~6/m7 - M6/~7 - M7 - P8
problematic because m3 is narrower than M2
13b-edo: C D * Cb Db (# = vvv) with sharp lowering the pitch, and major/aug narrower than minor/dim
C D E * * * F G A B * * * C
C - D - E - E^/F# - Ebv/F#^ - Eb/Fv - F - G - A - B - B^/C# - Bbv/C#^ - Bb/Cv - C
P1 - M2 - ^M2/M3 - vm2/^M3 - m2/vm3 - m3 - P4 - P5 - M6 - ^M6/M7 - vm6/^M7 - m6/vm7 - m7 - P8
problematic because M3 is narrower than m2
C D * C# D# (# = ^^^) with sharp raising the pitch, and major/aug wider than minor/dim
C - D - E - E^/Fb - E#v/Fb^ - E#/Fv - F - G - A - B - B^/Cb - B#v/Cb^ - B#/Cv - C
P1 - m2 - ^m2/m3 - vM2/^m3 - M2/vM3 - M3 - P4 - P5 - m6 - ^m6/m7 - vM6/^m7 - M6/vM7 - M7 - P8
problematic because m3 is narrower than M2
16edo: C Cb/D# D (# = v) with sharp lowering the pitch, and major/aug narrower than minor/dim
C * D * E * * F * G * A * B * * C
C - Cb/D# - D - Db/E# - E - Eb - F# - F - Fb/G# - G - Gb/A# - A - Ab/B# - B - Bb - C# - C
P1 - d1/A2 - M2 - m2 - M3 - m3 - d3/A4 - P4 - d4/A5 - P5 - d5/A6 - M6 - m6 - M7 - m7 - d7/A8 - P8
C C#/Db D (# = ^) with sharp raising the pitch, and major/aug wider than minor/dim
C - C#/Db - D - D#/Eb - E - E# - Fb - F - F#/Gb - G - G#/Ab - A - A#/Bb - B - B# - Cb - C
P1 - A1/d2 - m2 - M2 - m3 - M3 - A3/d4 - P4 - A4/d5 - P5 - A5/d6 - m6 - M6 - m7 - M7 - A7/d8 - P8
18b-edo: C/D# * Cb/D (# = vv) with sharp lowering the pitch, and major/aug narrower than minor/dim
C * D * E * * * F * G * A * B * * * C
C - C^/Dv - D - D^/Ev - E - E^ - Eb/F# - Fv - F - F^/Gv - G - G^/Av - A - A^/Bv - B - B^ - Bb/C# - Cv - C
P1 - ^P1/vM2 - M2 - ~2 - m2/M3 - ~3 - m3 - ^m3/vP4 - P4 - ^P4/vP5 - P5 - ^P5/vM6 - M6 - ~6 - m6/M7 - ~7 - m7 - ^m2/d8 - P8
Mid "~" is midway between major and minor, and replaces both upmajor and downminor.
C/Db * C#/D (# = ^^) with sharp raising the pitch, and major/aug wider than minor/dim
C - C^/Dv - D - D^/Ev - E - E^ - E#/Fb - Fv - F - F^/Gv - G - G^/Av - A - A^/Bv - B - B^ - B#/Cb - Cv - C
P1 - ^P1/vm2 - m2 - ~2 - mM2/m3 - ~3 - M3 - ^M3/vP4 - P4 - ^P4/vP5 - P5 - ^P5/vm6 - m6 - ~6 - M6/m7 - ~7 - M7 - ^M7/d8 - P8
23edo: C Cb * D# D (# = v) with sharp lowering the pitch, and major/aug narrower than minor/dim
C * * D * * E * * * F * * G * * A * * B * * * C
C - Cb - D# - D - Db - E# - E - Eb - Ebb/Fx - F# - F - Fb - G# - G - Gb - A# - A - Ab - B# - B - Bb - Bbb/Cx - C# - C
P1 - d1 - A2 - M2 - m2 - d2/A3 - M3 - m3 - d3 - A4 - P4 - d4 - A5 - P5 - d5 - A6 - M6 - m6 - d6/A7 - M7 - m7 - d7 - A8 - P8
C C# * Db D (# = ^) with sharp raising the pitch, and major/aug wider than minor/dim
C - C# - Db - D - D# - Eb - E - E# - Ex/Fbb - Fb - F - F# - Gb - G - G# - Ab - A - A# - Bb - B - B# - Bx/Cbb - Cb - C
P1 - A1 - d2 - m2 - M2 - A2/d3 - m3 - M3 - A3 - d4 - P4 - A4 - d5 - P5 - A5 - d6 - m6 - M6 - A6/d7 - m7 - M7 - A7 - d8 - P8
Pentatonic EDOs
(5, 10, 15, 20, 25 and 30)
All pentatonic EDOs use the usual chain of fifths: m2 - m6 - m3 - m7 - P4 - P1 - P5 - M2 - M6 - M3 - M7 etc.
Fb - Cb - Gb - Db - Ab - Eb - Bb - F - C - G - D - A - E - B - F# - C# - G# - D# - A# - E# - B# etc.
In all pentatonic EDOs, the minor 2nd = the unison and the major 3rd = the perfect fourth.
5edo: C/Db C#/D
B/C D E/F G A B/C
P1 - M2/m3 - P4 - P5 - M6/m7 - P8
10edo: 2 keys per sharp/flat: C/Db * C#/D
B/C * D * E/F * G * A * B/C
B/C - C^/Dv - D - D^/Ev - E/F - F^/Gv - G - G^/Av - A - A^/Bv - B/C
P1/m2 - ^m2/vM2 - M2/m3 - ^m3/vM3 - M3/P4 - ^P4/vP5 - P5/m6 - ^m6/vM6 - M6/m7 - ^m7/vM7 - P8
15edo: 3 keys per sharp/flat: C/Db * * C#/D
B/C * * D * * E/F * * G * * A * * B/C
B/C - C^ - Dv - D - D^ - Ev - E/F - F^ - Gv - G - G^ - Av - A - A^ - Bv - B/C
P1/m2 - ^m2 - vM2 - M2/m3 - ^m3 - vM3 - M3/P4 - ^P4 - vP5 - P5/m6 - ^m6 - vM6 - M6/m7 - ^m7 - vM7 - P8
20edo: 4 keys per sharp/flat: C/Db * * * C#/D
B/C * * * D * * * E/F * * * G * * * A * * * B/C
B/C - C^ - C^^/Dvv - Dv - D - D^ - D^^/Evv - Ev - E/F - F^ - F^^/Gvv - Gv - G - G^ - G^^/Avv - Av - A - A^ - A^^/Bvv - Bv - B/C
P1/m2 - ^m2 - ~2 - vM2 - M2/m3 - ^m3 - ~3 - vM3 - M3/P4 - ^P4 - ^^P4/vvP5 - vP5 - P5/m6 - ^m6 - ~6 - vM6 - M6/m7 - ^m7 - ~7 - vM7 - P8
25edo: 5 keys per sharp/flat: C/Db * * * * C#/D
B/C * * * * D * * * * E/F * * * * G * * * * A * * * * B/C
B/C - C^ - C^^ - Dvv - Dv - D - D^ - D^^ - Evv - Ev - E/F - F^ - F^^ - Gvv - Gv - G - G^ - G^^ - Avv - Av - A - A^ - A^^ - Bvv - Bv - B/C
P1/m2 - ^m2 - v~2 - ^~2 - vM2 - M2/m3 - ^m3 - v~3 - ^~3 - vM3 - M3/P4 - ^P4 - ^^P4 - vvP5 - vP5 - P5/m6 - ^m6 - v~6 - ^~6 - vM6 - M6/m7 - ^m7 - v~7 - ^~7 - vM7 - P8
30edo: 6 keys per sharp/flat: C/Db * * * * * C#/D
B/C * * * * * D * * * * * E/F * * * * * G * * * * * A * * * * * B/C
B/C - C^ - C^^ - Dvv - Dv - D - D^ - D^^ - Evv - Ev - E/F - F^ - F^^ - Gvv - Gv - G - G^ - G^^ - Avv - Av - A - A^ - A^^ - Bvv - Bv - B/C
P1/m2 - ^m2 - v~2 - ^~2 - vM2 - M2/m3 - ^m3 - v~3 - ^~3 - vM3 - M3/P4 - ^P4 - ^^P4 - vvP5 - vP5 - P5/m6 - ^m6 - v~6 - ^~6 - vM6 - M6/m7 - ^m7 - v~7 - ^~7 - vM7 - P8
Supersharp EDOs
(8, 11b, 13 and 18)
These can be notated with diatonic notation just fine.
Diatonic notation for 8edo, 11b-edo, 13edo and 18edo
Db - Ab - Eb - Bb - F - C - G - D - A - E - B - F# - C# - G# - D# etc.
8edo: (generator = 5\8 = perfect 5thoid) C B D
C B D F E G * A C
C B D F E G G^ A C
11b-edo: (generator = 7\11 = perfect 5thoid) C . B D
C * B D F * E G * * A C
13edo: (generator = 8\13 = perfect 5thoid) C B . D
C B * D * F E * G * * A * C
18edo: (generator = 11\18 = perfect 5thoid) C B . . D
C B * * D * * F E * * G * * * A * * C
Rank-2 Scales: 8ve Periods
Ups and downs can be used to notate rank-2 scales as well. Instead of edos like 12-edo, we'll be talking about frameworks like 12-tone. The generator chain is called a genchain. Fifth-generated rank-2 tunings can be notated without ups and downs in any framework on either side of the 4\7 kite (sharp-1 or flat-1):
12-tone genchain Eb Bb F C G D A E B F# C# G# makes this scale: C C# D Eb E F F# G G# A Bb B C
12-tone genchain F C G D A E B F# C# G# D# A# makes this scale: C C# D D# E F F# G G# A A# B C
When the notes selected from the genchain don't make a continuous chain, you get a MODMOS, easily notated:
7-tone: Eb * F C G D A * B = C D Eb F G A B C
5-tone: Bb * C G D * E = C D E G Bb C
12-tone: Gb Db * * Bb F C G D A E B * * G# D# = C Db D D# E F Gb G G# A Bb B C
For a rank-2 temperament to work with a given framework, the keyspans of the generator and the period must be coprime. Otherwise the genchain won't reach all the notes. The framework must be single-ring, i.e. not on the spine of a kite. For example, fifth-generated tunings like meantone and pythagorean are compatible with 12-tone, but not with 15-tone or 24-tone. Likewise a third-generated tuning like dicot or mohajira is incompatible with 12-tone, but compatible with 24-tone. In the region of the scale tree near the 2\7 kite, 12-tone is multi-ring and 24 isn't.
All supersharp frameworks are incompatible with fifth-generated heptatonic notation, since the minor 2nd becomes a descending interval. All perfect and pentatonic frameworks, except for 5-tone and 7-tone, are incompatible with fifth-generated rank-2 tunings. We need only consider single-ring regular frameworks with sharpness > 1 or < -1. If these are notated without ups and downs, the notes run out of order:
17-tone: Gb Db Ab Eb Bb F C G D A E B F# C# G# D# A# = C Db C# D Eb D# E F Gb F# G Ab G# A Bb A# B C
To extend ups and downs to rank-2 tunings, the up symbol is assigned not only a keyspan (always +1) but also a genspan, which indicates how many steps forward or backwards along the genchain one must travel to find the interval. The sharp is always genspan +7, and the flat is always genspan -7. By adding the genspans of the sharps/flats to the genspans of the ups/downs attached to a note, we can determine the exact location of the note on the genchain, and thus its exact tuning.
Every single-ring node on the scale tree heads up a kite and is on the side of two other kites. These two other kites can be used to find the rank-2 interval with keyspan of 1. For example, the 10\17 node is on the side of the 7\12 kite and the 3\5 kite (its two stern-brocot ancestors). Because it's on the right (fifthward) side of the 7\12 kite, we know that 12 fifths add up to 1\17. Because it's on the left (fourthward) side of the 3\5 kite, 5 fourths add up to 1\17. Between the two, choose the interval with the smaller genspan for simplicity, which is always the kite closest to the top of the diagram. Thus in the 17-tone framework, up has a genspan of -5, corresponding to five stacked fourths, octave-reduced, which equals a tempered pythagorean minor 2nd of 256/243. Because a minor 2nd equals an up, a downminor 2nd (vm2) equals no change, and can be freely added to or subtracted from any note to change its name. To avoid out-of-order notes, either rewrite C# as C# + vm2 = Dv, or rewrite Db as Db - vm2 = C^ (subtracting a down equals adding an up).
17-tone Gb - A# genchain = C C^ C# D D^ D# E F F^ F# G G^ G# A A^ A# B C = C Db Dv D Eb Ev E F Gb Gv G Ab Av A Bb Bv B C
Substituting E# for Gb in the genchain gives us E# + vm2 = F#v in place of F^ or Gb. Unlike 17edo, F#v is not equivalent to F^, even though they occupy the same key on the keyboard, just as C# equals Db in 12-edo but not 12-tone.
22-tone also has a pentatonic ancestor, and vm2 still equals a unison. The 22-tone genchain:
| genspan from C | keyspan from C | |||||
| -13 | 7 | Gbb | Fb^ | Eb^^ | ||
| -12 | 20 | Dbb | Cb^ | Bb^^ | ||
| -11 | 11 | Abb | Gb^ | F^^ | ||
| -10 | 2 | Ebb | Db^ | C^^ | ||
| -9 | 15 | Bbb | Ab^ | G^^ | ||
| -8 | 6 | Fb | Eb^ | D^^ | ||
| -7 | 19 | Cb | Bb^ | A^^ | ||
| -6 | 10 | Gb | F^ | E^^ | ||
| -5 | 1 | Db | C^ | B^^ | ||
| -4 | 14 | Ab | G^ | F#^^ | ||
| -3 | 5 | Fbv | Eb | D^ | C#^^ | |
| -2 | 18 | Cbv | Bb | A^ | G#^^ | |
| -1 | 9 | Gbv | F | E^ | D#^^ | |
| 0 | 0 | Dbv | C | B^ | A#^^ | |
| 1 | 13 | Abv | G | F#^ | E#^^ | |
| 2 | 4 | Fbvv | Ebv | D | C#^ | B#^^ |
| 3 | 17 | Cbvv | Bbv | A | G#^ | |
| 4 | 8 | Gbvv | Fv | E | D#^ | |
| 5 | 21 | Dbvv | Cv | B | A#^ | |
| 6 | 12 | Abvv | Gv | F# | E#^ | |
| 7 | 3 | Ebvv | Dv | C# | B#^ | |
| 8 | 16 | Bbvv | Av | G# | ||
| 9 | 7 | Fvv | Ev | D# | ||
| 10 | 20 | Cvv | Bv | A# | ||
| 11 | 11 | Gvv | F#v | E# | ||
| 12 | 2 | Dvv | C#v | B# | ||
| 13 | 15 | Avv | G#v | Fx | ||
| 14 | 6 | Evv | D#v | Cx | ||
| 15 | 19 | Bvv | A#v | Gx | ||
| 16 | 10 | F#vv | E#v | Dx | ||
| 17 | 1 | C#vv | B#v | Ax | ||
| etc. |
The 22-tone keyboard, with alternate tunings for the black keys:
| keyspan from C | genspan from C | note | genspan from C | note |
| 0 | 0 | C | ||
| 1 | -5 | Db = C^ | +17 | C#vv = Dv3 |
| 2 | -10 | Db^ = C^^ | +12 | C#v = Dvv |
| 3 | -15 | Db^^ = C^3 | +7 | C# = Dv |
| 4 | +2 | D | ||
| 5 | -3 | Eb = D^ | +19 | D#vv = Ev3 |
| 6 | -8 | Eb^ = D^^ | +14 | D#v = Evv |
| 7 | -13 | Eb^^ = D^3 | +9 | D# = Ev |
| 8 | +4 | E | ||
| 9 | -1 | F | ||
| 10 | -6 | Gb = F^ | +16 | F#vv = Gv3 |
| 11 | -11 | Gb^ = F^^ | +11 | F#v = Gvv |
| 12 | -16 | Gb^^ = F^3 | +6 | F# = Gv |
| 13 | +1 | G | ||
| 14 | -4 | Ab = G^ | +18 | G#vv = Av3 |
| 15 | -9 | Ab^ = G^^ | +13 | G#v = Avv |
| 16 | -14 | Ab^^ = G^3 | +8 | G# = Av |
| 17 | +3 | A | ||
| 18 | -2 | Bb = A^ | +20 | A#vv = Bv3 |
| 19 | -7 | Bb^ = A^^ | +15 | A#v = Bvv |
| 20 | -12 | Bb^^ = A^3 | +10 | A# = Bv |
| 21 | +5 | B | ||
| 22 | 0 | C |
In 22-tone, positive genspans, which lie on the fifthward half of the genchain, create sharps and downs. Negative genspans, from the fourthward half of the genchain, create flats and ups.
The three black keys between C and D each have two names, one some version of C and the other some version of D. You can choose which one you want to keep the notes in order. Here are four possible tunings of these 3 keys, each written out in four ways:
C C#vv C#v C# D = C C#vv C#v Dv D = C C#vv Dvv Dv D = C Dv3 Dvv Dv D
C C^ C#v C# D = C C^ C#v Dv D = C C^ Dvv Dv D = C Db Dvv Dv D
C C^ C^^ C# D = C C^ C^^ Dv D = C C^ Db^ Dv D = C Db Db^ Dv D
C C^ C^^ C^3 D = C C^ C^^ Db^^ D = C C^ Db^ Db^^ D = C Db Db^ Db^^ D
All four tunings could be part of a MOS. Here's one that requires a MODMOS:
C C^ C#v C^3 D = C C^ C#v Db^^ D = C C^ Dvv Db^^ D = C Db Dvv Db^^ D
There are hundreds of possibilities, and ups and downs can notate all of them.
Finding the up's genspan
The genspan for the up symbol in 22-tone can be found from the scale tree. Or it can be derived more rigorously if calculated from the keyspans:
K(^) = +1, K(v) = -1 (by definition, the keyspan of an up is 1)
K(#) = c, K(b) = -c (c = sharpness = keyspan of a sharp = how many keys wide aug1 is. For 22-tone, c = 3)
K(#vc) = K(#) + c * K(v) = 0 (going up c keys using a sharp, then going down c keys using c downs, must cancel out)
- vc means one sharp plus c downs. Zero keyspans in the genchain only occur on every Nth step for a N-tone framework. E.g., 12-tone keyspans:
| genchain of fifths | C | G | D | A | E | B | F# | C# | G# | D# | A# | E# | B# |
| genspan from C | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 12-tone keyspan from C | 0 | 7 | 2 | 9 | 4 | 11 | 6 | 1 | 8 | 3 | 10 | 5 | 0 |
B#, genspan 12, has a zero keyspan, as does Dbb, genspan -12, and A###, genspan 24. Thus the final equation means that the genspan resulting from going up a sharp and down c downs must be zero, N, -N, 2N, -2N, etc. Thus this genspan mod N must be zero.
G(#) = 7 (by definition, the sharp's genspan = 7, since we're assuming heptatonic notation)
G(#vc) = G(#) + c * G(v) = G(#) - c * G(^) = 7 - c * G(^)
G(#vc) mod N = 0, thus G(#vc) = i * N for some integer i
7 - c * G(^) = i * N
G(^) = - (i * N - 7) / c
For 22-tone, N = 22 and c = 3. We choose i to be the smallest (least absolute value) number that avoids fractions, and produces an interval with a keyspan of 1. Thus i = 1, G(^) = -5, and ^ = min 2nd. In order to provide alternate names for each note, the ^ should always be a 2nd, or a descending 2nd which is a 7th. This means the up's genspan modulo 7 should be 2 or 5. However as we'll see, this isn't always possible.
All relevant frameworks of size 53 or less:
| Keyspan of # | value of i | genspan of ^ | example | stepspan &
quality of ^ |
stepspan &
quality of unison | |
| 11-tone | -2 | 1 | 2 | C^ = D | maj 2nd | vM2 |
| 13b-tone | -3 | 1 | 2 | C^ = D | maj 2nd | vM2 |
| 17-tone | 2 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 22-tone | 3 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 27-tone | 4 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 29-tone | 3 | -1 | +12 | C^ = B# | desc dim 2nd | ^d2 |
| 31-tone | 2 | 1 | -12 | C^ = Dbb | dim 2nd | vd2 |
| 32-tone | 5 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 37-tone | 6 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 39-tone | 5 | -2 | +17 | C^ = Ax | desc double-dim 3rd | ^dd3 |
| 41-tone | 4 | -1 | +12 | C^ = B# | desc dim 2nd | ^d2 |
| 42-tone | 7 | 1 | -5 | C^ = Db | min 2nd | vm2 |
| 43-tone | 3 | 1 | -12 | C^ = Dbb | dim 2nd | vd2 |
| 45-tone | 2 | 1 | -19 | C^ = Dbbb
|
double-dim 2nd | vdd2 |
| 49-tone | 7 | -3 | +22 | C^ = G### | desc triple-dim 4th | ^ddd4 |
| 50-tone | 3 | -1 | +19 | C^ = Bx | desc double-dim 2nd | ^dd2 |
| 53-tone | 5 | -1 | +12 | C^ = B# | desc dim 2nd | vd2 |
A look at the scale fragments reveals why 29-tone's up is a descending interval:
22-tone: C Db * C# D
27-tone: C Db * * C# D
29-tone: C * Db C# * D
The 22-tone and 27-tone frameworks all have Db adjacent to C, so that C^ equals Db. For 29-tone, Db = C^^. To find a D-something that is adjacent to C, we must use Dbb, which is one key below C. Thus Cv = Dbb, and C^ = B#, ^ is a descending dim 2nd, and the unison is an up-dim 2nd, ^d2. Descending ups are not a problem.
The 29-tone keyboard, with alternate tunings for the black keys:
| keyspan from C | genspan from C | note | genspan from C | note |
| 0 | 0 | C | ||
| 1 | -17 | Dbv = C#vv | +12 | C^ |
| 2 | -5 | Db = C#v | +24 | C^^ = Dbb^3 |
| 3 | -22 | Dvv = Cxv3 | +7 | C# = Db^ |
| 4 | -10 | Dv | +19 | C#^ = Db^^ |
| 5 | +2 | D | ||
| etc. |
The value of i equals the stepspan of the up interval. 39-tone and 49-tone are problematic:
39-tone: C * Db * * C# * D
49-tone: C * Db * * * * C# * D
There is no variant of D adjacent to C, and there is no 2nd with keyspan 1 or -1. (In theory, 39-tone's C^ could be an octuple-diminished 9th.) Notating rank-2 fifth-generated tunings in these two frameworks requires out-of-order notes.
Rank-2 Scales: Non-8ve Periods
This section is somewhat obsolete, see the pergens page instead.
Fractional-period rank-2 temperaments have multiple genchains running in parallel. Multiple genchains occur because a rank-2 genchain is really a 2 dimensional "genweb", running in octaves (or whatever the period is) vertically and fifths (or whatever the generator is) horizontally.
F2 --- C3 --- G3 --- D4 --- A4 --- E5 --- B5
F1 --- C2 --- G2 --- D3 --- A3 --- E4 --- B4
F0 --- C1 --- G1 --- D2 --- A2 --- E3 --- B3
When the period is an octave, the genweb octave-reduces to a single horizontal genchain:
F --- C --- G --- D --- A --- E --- B
But if the period is a half-octave, the genweb has vertical half-octaves, which octave-reduces to two parallel genchains. Temperaments with third-octave periods reduce to a triple-genchain, and so forth.
Ups and downs can be used to indicate the genchain. This is a completely separate use of ups and downs than in the last section! Rather than a genspan, the up has a "period-span" of 1. Each genchain has a different "height"; one is up, another is down, etc.
For example, Srutal [10] might look like this:
F^3 --- C^4 --- G^4 --- D^5 --- A^5
C3 ---- G3 ----- D4 ---- A4 ---- E5
F^2 --- C^3 --- G^3 --- D^4 --- A^4
C2 ---- G2 ----- D3 ---- A3 ---- E3
F^1 --- C^2 --- G^2 --- D^3 --- A^3
C1 ---- G1 ----- D2 ---- A2 ---- E2
This octave-reduces to two genchains:
F^ --- C^ --- G^ --- D^ --- A^
C ---- G ----- D ---- A ---- E
Scale: C - C^ - D - D^ - E - F^ - G - G^ - A - A^ - C
Moving up from C to F^ moves up a half-octave. Ups and downs are used (F^ not F#) because F# is on the wrong genchain. It's two steps to the right of E. The exact meaning of "up" here is "a half-octave minus a fourth", with the understanding that both the octave and the fourth may be tempered. Normally, the 12-tone half-octave would be A4 or d5, no ups or downs needed. But to notate this tuning, the half-octave must be written ^4 or v5.
If "up" means "a half-octave minus a fourth" as well as "up one key or fret", a 4th must be one key or fret less than a half-octave, which only holds for frameworks 10, 12, 14, 16 and 18b. For other frameworks, the period must be named differently. The general rule is, the period's name must have at least one up or down, and the generator's name must have none, or vice versa. This allows ups and downs to serve "double-duty" as genchain indicators. For 20-tone, the period is ^^4 or vv5. For 22-tone, it's vA4 or ^d5. For 24, 26 and 28, it's ^^4 or vv5. But for now, let's assume the period is ^4 or v5.
It would be equally valid to write the half-octave not as an up-fourth but as a down-fifth:
Gv --- Dv --- Av --- Ev --- Bv
C ----- G ----- D ---- A ---- E
It would also be valid to exchange the two rows:
C ----- G ----- D ---- A ---- E
Gv --- Dv --- Av --- Ev --- Bv
Srutal's generator could be thought of as either ~3/2 or ~16/15, because ~16/15 would still create the same scales:
F^ -- G --- G^ -- A --- A^
C --- C^ -- D --- D^ -- E
The Diminished [8] scale has only two modes. The period is a quarter-octave = 300¢. The generator is ~3/2. There are four very short genchains.
G#vv ----- D#vv
Ev --------- Bv
C ---------- G
Ab^ ------- Eb^
Scale: C - D#vv - Ev - Eb^ - G#vv - G - Ab^ - Bv - C
The period interval is named as a 3rd with at least one up or down. Again, it varies by framework. For 12-tone, it's a downmajor 3rd, as above. For 16-tone, vm3, for 20-tone, ^m3, for 24-tone, vvM3. For a vM3, "up" means "a major 3rd (~81/64) minus a quarter-octave". Using ~25/24 as the generator yields the same scale.
Blackwood [10]'s period is a fifth-octave, and the generator is ~5/4. Here it's better if ups and downs indicate the generator-span instead of the period-span. "Up" means "2/5 of an octave minus ~5/4":
F ------ Av
D ------ F#v
C ------ Ev
A ------ C#v
G ------ Bv
Since octaves are equivalent, the lattice rows can be reordered to make a "pseudo-period" of 3\5 = ~3/2.
F ------ Av
C ------ Ev
G ------ Bv
D ------ F#v
A ------ C#v
The scale: C C#v D Ev F F#v G Av A Bv C
Ups and downs solfege
Solfege (do-re-mi) can be adapted to indicate sharp/flat and up/down:
The initial consonant remains as before: D, R, M, F, S, L and T
The first vowel indicates sharp or flat: a = natural, e = #, i = ##, o = b, u = bb
The vowels are pronounced as in Spanish or Italian
The pitch from ## to bb follows the natural vowel spectrum i-e-a-o-u
The optional 2nd vowel indicates up/down: a = ^^^, e = ^, i = ^^, o = v, u = vv
The 2nd vowel is separated from the first by either a glottal stop, an "h", a "w", or a "y"
Thus C#v is Deo, pronounced as De'o or Deho or Dewo or Deyo.
This suffices for many but not all edos, as some require triple sharps or quadruple ups.
Fixed-do solfege:
Da = C, De = C#, Di = C##, Do = Cb, Du =Cbb
Da = C, Da'e = C^, Da'i = C^^, Da'o = Cv, Da'u = Cvv, Da'a = C^^^
De = C#, De'e = C#^, De'i = C#^^, De'o = C#v, De'u = C#vv, De'a = C#^^^
etc.
Moveable-do solfege:
The 2nd vowel is as before. The 1st vowel's meaning depends on the interval.
Perfect intervals (tonic, 4th, 5th and octave): a = perfect, e= aug, i = double-aug, o = dim, u = double-dim
Da = P1, De = A1, Di = AA1, Do = d1, Du = dd1
Da'e = ^P1, Da'i = ^^P1, Da'o = vP1, Da'u = vvP1, Da'a = ^^^P1
etc.
Imperfect intervals (2nd, 3rd, 6th and 7th): a = major, e = aug, i = double-aug, o = minor, u = dim
Ra = M2, Re = A2, Ri = AA2, Ro = m2, Ru = d2
Ra'e = ^M2, Ra'i = ^^M2, Ra'o = vM2, Ra'u = vvM2, Ra'a = ^^^M2
etc.