User:FloraC/Proposed standard ear-training waveform
In October 2021, the default waveform in Scale Workshop was set to semisine, a super intriguing decision indeed. I expected the developers to openly talk about it, or at least update the user manual to include a few words. Such a thing never came about. Thereby I would like to share my own research results and opinions.
Chapter I. What
Up to the above chronological point, it is safe to say the semisine wave is a very obscure entity. It is not mentioned on Wikipedia at all, and Google search only reveals really limited materials about it.
To grab an impression, the waveform looks much like the fully rectified sine wave, and it is probably from that observation that the name was derived. In fact, however, it is made up of copies of parabolas. From this perspective, the name of the waveform is a little bit strange.
Of course, the main interest is in its frequency domain properties. In terms of Fourier series, it is
[math]\displaystyle{ \displaystyle f(t) = \sum_{\omega = 1}^{\infty} \cos ({\tau}\omega t)/\omega^2 }[/math]
The most salient fact is that it is composed of all integer harmonics with quadratic roll-off. If the base frequency has unity amplitude, the 2nd harmonic has 1/4, the 3rd harmonic has 1/9, and so on.
Let us not forget to take a sneak peek at Scale Workshop's implementation. Clearly, we are informed of what each number means in the line defining the sound:
// first element is DC offset, second element is fundamental, third element is 2nd harmonic, etc.
and the line of semisine reads:
new Float32Array([0, 1, 0.25, 0.111111, 0.0625, 0.04, 0.027777, 0.020408, 0.015625, 0.0123456, 0.01, 0.008264, 0.0069444, 0.0059171, 0.005102041, 0.0044444, 0.00390625])
Oh. Alright! So it is additive synthesis with the first 16 harmonics only…
Chapter II. Why
Commonly believed, there are "four basic waveforms": sine, sawtooth, square, and triangle. It is not quite right if you think about it. The only truly basic wave form is sine; the other three are composite. Their frequency-domain characteristics are:
- sawtooth – integer harmonics, linear roll-off,
- square – odd harmonics, linear roll-off,
- triangle – odd harmonics, quadratic roll-off.
We may think of sine as trivial, and the other three as basic, but we are missing the last piece of the puzzle, with integer harmonics and quadratic roll-off – semisine. Apart from sine, the picture of basic waveforms should be like as follows.
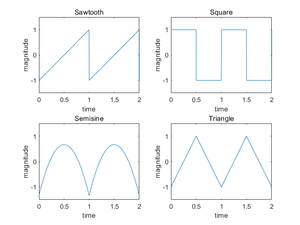
If you have not heard those waveforms, it is recommended to do so. Notably, sawtooth sounds very harsh and piercing; square is crunchy. They are commonly used as the bases in subtractive synthesis for a good reason. Meanwhile, triangle, whose higher harmonics are a little bit hard to notice, is a dark sound all things considered. In comparison, semisine hits a really pleasant acoustic sweet spot.
I have taken to believe that semisine is a general-purpose musical waveform, and the best candidate for a standard ear-training waveform. With all integer harmonics, it is a natural manifestation of the harmonic series. The quadratic roll-off produces a brightness just about right. Also, in terms of filter parameters, it corresponds to a lowpass filter of
[math]\displaystyle{ \displaystyle 20\lg (2^{-2}) \text{ dB/oct} = -12.04 \text{ dB/oct} }[/math]
which is virtually the standard filter roll-off in synthesis.
Chapter III. How
It is not clear why this waveform has tended to be overlooked. Maybe people only focus on synthetically useful waveforms. Anyway, we try to make the sound with the other waveforms in this section.
Apparently, we can simply superpose individual harmonics… but additive synthesis is generally intolerably inefficient – to clarify, harmonics beyond 16 may not be hard clipped, despite that I am less fond of talking about them. The absence of harmonics in the waves is not the same as not playing the notes, let alone what it means to those who actively use higher-limit JI.
Another possible approach is to take the sawtooth and apply a lowpass filter of -6 dB/oct (because sawtooth itself has -6 dB/oct), but this kind of filter is not common.
My method exploits the fact that semisine can be decomposed into an infinite series of triangle waves. It is like adding individual harmonics, but adding triangles is significantly more efficient. First, putting a triangle gives us odd harmonics with quadratic roll-off. Next, we add another triangle on the 2nd harmonic, attenuated to 1/4 of the base. At this point, we have every harmonic at the desired level except for multiples of 4, which are completely absent. Good thing is, it sounds somewhat like semisine already. Now we know what to do: we add another triangle on the 4th harmonic, attenuated to 1/16 of the base, and so forth ad infinitum.
The brightness of any finite synthesis made this way is between that of triangle and semisine. It is always brighter than triangle and darker than semisine. This series contains no terrible sound, and still it rapidly converges to semisine. Three iterations yield a saturated sound already. Since many synthesisers come with three oscillators, it is good point to stop. In this case, the missing harmonics are 8, 16, 24, 32… musically unimportant anyway. I would apply a -12 dB/oct lowpass filter with cutoff frequency at D9 (9397.273 Hz) to further attenuate the relatively harsh treble. I have created this sound in both Surge and Odin 2, the two free software synthesisers I use as workhorses.
Credits
Special thanks to Sintel.
Release Notes
© 2022 Flora Canou
Version Stable 1
This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License.