IFDO
An IFDO (inverse-arithmetic frequency division of the octave), or UDO (utonal division of the octave) is a periodic tuning system which divides the octave according to the inverse-arithmetic progression of frequency.
The inverse-arithmetic progression is known in general mathematics as the harmonic progression, but it would have been confusing to name this tuning a "harmonic division of the octave" because this mathematical sense of harmonic conflicts with the relevant musical sense of harmonic: divisions according to the harmonic mean correspond to subharmonic sequences, which are the opposite of harmonic sequences. And so "inverse-arithmetic progression" was coined to avoid this conflict, as well as to point to its relationship with the arithmetic progression.
For example, in 12ifdo the first degree is 24/23, the second is 24/22 (12/11), and so on. For an IFDO system, the difference between inverse interval ratios is equal (they form an inverse-arithmetic progression), rather than their difference between interval ratios being equal as in AFDO systems (an arithmetic progression). All IFDOs are subsets of just intonation, and up to transposition, any IFDO is a superset of a smaller IFDO and a subset of a larger IFDO (i.e. n-ifdo is a superset of (n - 1)-ifdo and a subset of (n + 1)-ifdo for any integer n > 1).
When treated as a scale, the IFDO is equivalent to the undertone scale, also known as an aliquot scale[1]. However, an undertone scale often has an assumption of a tonic whereas an IFDO simply describes all the theoretically available pitch relations. Therefore, a passage built on 1/(12::22) could be said to be in Mode 12, but is technically covered by 11ifdo.
An IFDO is equivalent to a UDO (utonal division of the octave). It may also be called an n-ELDO (equal length division of the octave) since it includes the pitches found by dividing the length of a string or resonating chamber into n equal parts; however, this more general acronym is typically reserved for divisions of irrational intervals (unlike the octave) which are therefore not subsets of just intonation.
Formula
Within each period of n-ifdo, the frequency ratio c of the k-th step is
[math]\displaystyle{ \displaystyle c = (2n)/(2n - k) }[/math]
Equal divisions of length
The equal division of length (EDL) is equivalent to the IFDO. However, n-edl corresponds to (n/2)-ifdo for any even number n. Therefore, EDL cannot be used to represent an odd-numbered IFDO.
n-edl divides a string length to n equal divisions, so we have n/2 divisions per octave. If the first division is l1 and the last, ln, we have:
- l1 = l2 = l3 = … = ln
So the sum of divisions is l or the string length. Note that the number of divisions in octave is half of the string length. By dividing a string length of l to n divisions we have:
- n:(n - 1):(n - 2):(n - 3):…:(n - m):…:1
where n - m is n/2.
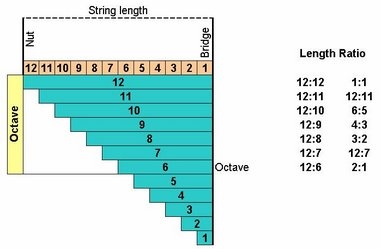
For example, by dividing string length to 12 equal divisions we have a series as:
- 12:11:10:9:8:7:6:5:4:3:2:1
which shows 12-edl:
12:12 means 12 from 12 divisions, 12:11 means 11 from 12 divisions and so on. Ratios as 12:11 shows active string length for each degree, which is vibrating. EDL system shows ascending trend of divisions sizes due to its inner structure and if compared with EDO:
Relation to superparticular ratios
An IFDO has step sizes of superparticular ratios with decreasing numerators. For example, 5ifdo has step sizes 10/9, 9/8, 8/7, 7/6, and 6/5.
Relation to utonality and subharmonic series
We can consider an IFDO system as a utonal system. Utonality is a term introduced by Harry Partch to describe chords whose notes are the undertones (divisors) of a given fixed tone. Considering IFDO, a utonality is a collection of pitches which can be expressed in ratios that have the same numerators. For example, 7/4, 7/5, 7/6 form an utonality in which 7 as the numerator is called a "numerary nexus".
Properties
- n-ifdo has maximum variety n.
- Except for 1ifdo and 2ifdo, IFDOs are chiral. The inverse of n-ifdo is n-afdo.
- 1ifdo is equivalent to 1afdo and 1edo;
- 2ifdo is equivalent to 2afdo.
Individual pages for IFDOs
By size
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
| 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |
| 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 |
| 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 |
| 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 |
| 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 |
| 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 |
| 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 |
| 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
| 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 |
| 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 |
| 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 |
By prime family
Under-2: 2, 4, 8, 16, 32, 64, 128, 256, 512
Under-3: 3, 6, 12, 24, 48, 96, 192, 384
Under-5: 5, 10, 20, 40, 80, 160, 320
Under-7: 7, 14, 28, 56, 112, 224, 448
Under-11: 11, 22, 44, 88, 176, 352
Under-13: 13, 26, 52, 104, 208, 416
Under-17: 17, 34, 68, 136, 272, 544
Under-19: 19, 38, 76, 152, 304
Under-23: 23, 46, 92, 184, 368
Under-29: 29, 58, 116, 232, 464
Under-31: 31, 62, 124, 248, 496
By other properties
Prime: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271
Semiprime: 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87, 91, 93, 94, 95, 106, 111, 115, 118, 119, 121, 122, 123, 129, 133, 134, 141, 142, 143, 145, 146, 155, 158, 159, 161, 166, 169, 177, 178, 183, 185, 187
Odd squarefree semiprime: 15, 21, 33, 35, 39, 51, 55, 57, 65, 69, 77, 85, 87, 91, 93, 95, 111, 115, 119, 123, 129, 133, 141, 143, 145, 155, 159, 161, 177, 183, 185, 187, 201, 203, 205, 209, 213, 215, 217, 219, 221, 235, 237, 247, 249, 253, 259, 265, 267, 287, 291, 295, 299, 301, 303
Prime powers (without primes): 4, 8, 9, 16, 25, 27, 32, 49, 64, 81, 121, 125, 128, 169, 243, 256, 289, 343, 361, 512, 529, 625, 729, 841, 961, 1024, 1331, 1369, 1681, 1849, 2048
See also
- Through other Pythagorean means:
- UD, or utonal division
External links
Notes
- ↑ 1/1, The Journal of the Just Intonation Network, Volume 4, Number 1, Winter 1988, p.6, Michael Sloper.