Stern-Brocot ancestors and rank 2 temperaments

Rank 2 tunings

Let's say you have a rank 2 tuning, with a period of P cents and a generator of G cents. You construct an N-note scale with a chain of N-1 generators. The classic example of this is a diatonic scale with an octave as period and a fifth as generator, with P = 1200¢, G = 702¢, and N = 7. Or perhaps the fifth is tempered down to 700¢ for 12-EDO, or 696¢ for 50-EDO meantone. Or perhaps N = 5 because you live in a pentatonic culture. Or N = 12 because you're creating a full keyboard tuning, not just a scale. Or perhaps you're using the third 5/4 as your generator. Or the tritave 3/1 as your period. Whatever, this discussion applies to all these cases. But for now we'll assume that the period is an octave and the generator is a roughly fifth-sized interval.

The process of filling in the period with notes can be visualized as drawing a star of sorts in a circle. Think of a clock. An octave is 12 hours and a fifth is about 7 hours. To construct a scale, draw a line from 12:00 noon to 7:00 to 2:00 to 9:00 to 4:00. Return back to noon with a dotted line. If noon is F, you've made a pentatonic scale F G A C D F. The first four lines you drew were generators, but the dotted line is a different interval. (Sometimes it works out that that dotted line is also a generator, but it usually isn't.) The first four lines are perfect fifths and the dotted line is a minor sixth E-C. Now erase the dotted line, and continue from 4:00 to 11:00 to 6:00, and a dotted line from 6:00 back to noon. That's a diatonic, aka heptatonic, scale F G A B C D E F. We drew six generators and a non-generator. In musical terms, six perfect fifths and a diminished fifth B-F.

Because the fifth may not be exactly 700¢, the line may not hit 7:00 exactly. That error will add up as we draw the star, so if the star misses 7:00 by a tiny bit, it will miss 6:00 by six times as much. But as long as the tiny bit is small, it won't matter. The shape of the star will be the same.

N is called the stepspan of the period. The stepspan is one less than the degree, so a third has stepspan 2, a fourth has stepspan 3, etc. We'll use stepspan instead of degree because it makes the math a little easier. The generator has a stepspan too, determined by how many star-points fall between our starting point 12:00 and the first generator at 7:00. Let's call this stepspan M. If N = 7, M = 4, because our heptatonic scale has four steps from C to G. For the pentatonic scale, N = 5 and M = 3.

Ideally, every time we draw a line on the clock face, the stepspan of that interval is M. Even the dotted line. But it's possible for some of the generators to have a different stepspan, which makes the scale hard to notate. If all the generators have the same stepspan, it's a MOS scale.

To see why the standard diatonic scale is MOS, go back to the 7-pointed star. First list the names of the 7 star-points:

scale steps: F G A B C D E

Now list these seven notes in the order that the star connects them:

generator chain: F C G D A E B

Take any 2 adjacent notes from this second list and find them on the first list, and they will indeed form a fifth in the sense that one note is five notes away from the other one. For example, the 1st and 2nd notes of the second list are F and C. On the first list, we have F-G-A-B-C, five notes. The 2nd and 3rd notes are C and G. Starting on C and wrapping around, we have C-D-E-F-G, again five notes. In other words, there is a fixed relationship between distance on one list and distance on the other list. This seemingly trivial fact is the fundamental principle behind our diatonic notation. This relationship holds for any distance. For example, take any two notes from the second list that have one other note between them, like the 1st and 3rd notes, F and G. Any such pair will be adjacent on the first list. This works the other way too. Take any two adjacent notes from the first list, like F and G, or A and B. They will always have one other note between them on the second list (F-C-G or A-E-B).

Each interval has what can be called a generator-span, or genspan for short, and vice versa. As we saw, F-G maps to F-C-G, thus the 2nd has genspan 2. The fifth has genspan 1, the major 3rd has genspan 4, etc. Each genspan creates a specific interval: 1 generator = a fifth, 2 gens = a major 2nd, etc. Going backwards on the generator-chain creates negative genspans, so -1 gen = 4th, and -2 gens = minor 7th. You can think of negative genspans as using an inverse generator. In this example the 4th is the inverse of the 5th. You can reach any interval by going either forwards or backwards, so every interval has two genspans associated with it, one positive and one negative. The two genspans are always exactly N steps apart. For example the 3rd is either 4 steps forwards or 3 steps back, a distance of 7. In this example, the positive genspan's interval is perfect, major or augmented, and the negative one is perfect, minor or diminished. For example, 4 steps forwards = major 3rd and 3 steps back = minor 3rd. Here's the complete list:

Intervals as genspans:

min 2nd = -5 gens, maj 2nd = 2 gens

min 3rd = -3, maj 3rd = 4

4th = -1, aug 4th = 6

dim 5th = -6, 5th = 1

min 6th = -4, maj 6th = 4

min 7th = -2, maj 7th = 5

dim 8ve = -7, 8ve = 0

Genspans as intervals:

-7 gens = dim octave, -6 gens = dim 5th, -5 = min 2nd, -4 = min 6th, -3 = min 3rd, -2 = min 7th, -1 = 4th, 0 = unison, 1 = 5th, 2 = maj 2nd, 3 = maj 6th, 4 = maj 3rd, 5 = maj 7th, 6 = aug 4th, 7 = aug unison

What's the criteria for MOS-ness? It has to do with M, N, G and P. It turns out that the generator must be roughly M/N of a period. In other words, G/P must be roughly M/N. Or to put it another way, M/N must be roughly G/P. Think of it this way: when we define 2/1 as an octave containing 7 steps, and 3/2 as a fifth containing 4 steps, we're saying that 3/2 is approximately four sevenths of 2/1. We're doing more than just saying it, we're basing our entire notation on it. Now a fifth isn't four-sevenths of an octave, not unless you flatten the heck out of it, but we can get away with saying it is because it's roughly four-sevenths. It's close enough to generate a MOS heptatonic scale.

Pentatonic cultures define 2/1 as containing 5 steps and 3/2 as containing 3 steps. They approximate the fifth as three-fifths of an octave, and it works. Pentatonic scales are MOS.

What if we said that 2/1 is a ninth of 8 steps, and 3/2 is a sixth of 5 steps? This would be an octotonic scale. What happens when you draw an eight-pointed star on a clock? You go noon to 7:00 to 2:00 to 9:00 to 4:00 to 11:00 to 6:00 to 1:00 and a dotted line back to noon. The dotted line from 1:00 to noon is NOT a sixth! Neither is 2:00 to 9:00, or 4:00 to 11:00, because there aren't enough steps in between them. So if M = 5, N = 8, P = 1200¢ and G = about 702¢, we get a non-MOS scale. For the five-eighths approximation to work, G/P would have to be closer to 5/8, and our generator would need to be significantly sharper than 702¢.

What's wrong with non-MOS scales? Some of the generators are fifths and some are sixths, naming them by the number of scale steps they contain. And the last line is a seventh. But wait, you say, doesn't that happen in our standard system? Isn't a tritone both an aug 4th and a dim 5th? Yes, but remember that only in certain tunings (12-EDO, 24-EDO, 36-EDO, etc.) is the aug4 identical to the dim5. Often they are different intervals. But our octotonic generators are always identical by definition. More on this later.

So four-sevenths works for the fifth, but five-eighths doesn't. How accurate does this M/N approximation have to be? What are the exact limits of what G can be? How flat or sharp can our fifth be and still make a MOS heptatonic scale? Or to put it another way, how sharp would the generator have to be for five-eighths to work?

It turns out that if the scale is MOS, M and N are always co-prime, meaning no common factors. If they weren't, the star wouldn't hit all the points before returning to noon. For example, if N = 10 and M = 6, your star would only hit 5 out of the 10 points. Another example: we've drawn a 5-pointed star and a 7-pointed star on a clock. Try drawing a 6-pointed star, as symmetrical as the other stars. The Star of David doesn't count, because you must draw it all in one go, without lifting your pencil from the page. Give up yet? It can't be done. That's because 2, 3 and 4 aren't co-prime with 6. The only numbers smaller than 6 that are co-prime with it are 1 and 5. Using those numbers is equivalent to drawing a hexagon in a circle. A musically valid generator, but not very star-like.

If you draw a MOS-scale star on a clock, at some point you reach the point to the immediate right of the starting point at noon, the 2nd note of the scale. Let's say that point is after you draw X lines. Mathematically speaking, we say there exists a number X between 0 and N such that XM mod N = 1. X must be less than N because after N lines, we've drawn the whole star. In the course of drawing these X lines, we have probably gone around the clock a number of times. In musical terms, we probably need to octave-reduce the sum of X generators to make a 2nd, as opposed to a 9th or something. Let's say we've gone around the clock Y times. We need to reduce X generators by Y periods, and we say XM - YN = 1, or XM = YN + 1. Y will always be less than M, because we go around the clock M times total. We know this because NM = MN, so N generators = M periods.

Now at some other point while drawing, you reach the point to the immediate left of 12:00 noon, which is the 7th, or more generally the penultimate note of the scale. How many lines does it take? We want an equation like XM = YN + 1, except with - 1 instead of +1, and different X and Y of course. It turns out that N - X generators is just shy of M - Y periods. Proof:

#1	XM = YN + 1
#2	NM = MN
subtract #1 from #2:	NM - XM = MN - YN - 1
rewrite it	(N - X) M = (M - Y) N - 1

So far we've been thinking of the generator only as an M-step interval. But it's actually an interval of G cents. If you make the generator flatter (or narrower, strictly speaking), all the intervals of the scale become flatter. If you flatten the generator to the point that the scale becomes non-MOS, your 2nd will be flattened down to the tonic. If this happens, X generators will be equal to Y periods, in other words, XG = YP. Thus the lower limit of what G can be is (Y/X) P.

If you make the generator sharper (or wider), all the intervals become sharper. If you sharpen the generator to the non-MOS point, the penultimate note becomes equal to the period, and N - X generators will equal M - Y periods. Thus (N - X) G = (M - Y) P, and the upper limit of what G can be is [(M - Y) / (N - X)] P. Thus:

Y / X < G / P < (M - Y) / (N - X)

Let's apply this to a heptatonic scale generated by a fifth. If N = 7 and M = 4, 4X mod 7 = 1 is true when X = 2. If 4X = 7Y + 1, then Y = 1. N - X is 5 and M - Y is 3. Thus 1/2 < G/P < 3/5. P = 1200¢, so the generator must be between 600¢ and 720¢. By symmetry we can deduce that if M = 3, the generator (the 4th) must be 480-600¢. Although we used the ratio 2/1 to derive 1200¢, we didn't use 3/2 or 702¢ anywhere in our calculations. We simply said that our 7-pointed star must have lines that go about 4/7 of the way around the clock. We could use as our generator any ratio that falls in the 600-720¢ range, such as 10/7 or 16/11. We could also use any irrational interval in this range, such as the EDO intervals 7\12 or 11\19 or 13\22. As long as we assign a stepspan of 4 to the generator, the scale will be MOS. In other words, we're using the term "fifth" in the loosest possible sense, meaning any note-to-note interval that skips over 3 other notes and is 600-720¢.

Let's try this for pentatonic scales: N = 5 and M = 3. X is again 2, and Y is again 1. N - X is 3 and M - Y is 2. The limits for G are (1/2)1200 = 600¢ and (2/3)1200 = 800¢. The lower limit is the same, but the upper limit is higher for pentatonic than for heptatonic, meaning it's more robust. Thus a generator of 14/9 = 765¢ would make a MOS pentatonic scale but an non-MOS heptatonic scale. As would an 8-EDO generator of 5\8 = 750¢.

Let's take another look at non-MOS scales, using the 5\8 interval to generate a 7-note scale. On the clock face, 5\8 equals 7 and 1/2 hours. Starting at noon, draw lines to 7:30 to 3:00 to 10:30 to 6:00 to 1:30 to 9:00 and a dotted line back to noon. Name the star-points F G A B C D E as before, and also list the notes in the order that the star connects them:

scale steps: F G A B C D E F

generator chain: F C A E B G D F

Here's the problem: on the gen-chain, F-C and C-A are both adjacent pairs. But F-C is a fifth, but C-A is a sixth. Adjacent pairs A-E and E-B are fifths, but B-G is a sixth. G-D is a fifth, but the dotted line D-F is only a third. Imagine trying to notate this scale that way. You'd have to look at C-G, A-E and E-B and think "looks like a fifth but sounds like a tritone". You'd have to look at C-A and B-G and think "looks like a major or minor sixth but sounds like a fifth". Furthermore, all the other intervals are also inconsistent. For example, the F-A third is the same size as the A-B second. This is all because distance on one list is no longer related to distance on the other list. As a result, you can't use the familiar interval arithmetic that you've spent years memorizing. You'd be much better off drawing a five-pointed star and using the letters F G A C D, because that would be MOS:

scale steps: F G A C D F

generator chain: F C G D A F

Please don't think that I'm saying that good music can't be made with an 8-EDO scale. I'm just saying that if you make music with this scale, it's much easier to write it out pentatonically than heptatonically.

Back to heptatonic, what if the generator was a third? Then M = 2, and X = 4 and Y = 1. N - X = 3 and M - Y = 1. The limits of G are 1/4 and 1/3, which is 300-400¢. Thus the ratios 6/5, 5/4, or 11/9, or the EDO-steps 3\10, 4\13 or 5\17 would all be valid generators. 7/6 would not work, it's too small. Would it work as a 2nd, with M = 1?

If M = 1, we can find the limits very easily. X is always 1 and Y is always 0. The lower limit is 0/1 = 0¢, in other words any interval at all will be big enough. The upper limit is 1/(N - 1). For N = 7, the upper limit is 1/6 P = 200¢. So 7/6 wouldn't work heptatonically because it's too big to be a 2nd and too small to be a 3rd. But pentatonically, the upper limit is 1/4 P = 300¢, and 7/6 would work as a 2nd.

We can also find the limits easily when M = N - 1. X is always N - 1, because XM mod N = (N - 1) (N - 1) mod N = (N^2 -2N + 1) mod N = 1. Y is always N - 2 because XM = YN + 1, so Y = (XM - 1) / N = (N^2 - 2N + 1 - 1) / N = N - 2. The limits are (N - 2) / (N - 1) and 1/1. For heptatonic scales, M = 6 and the limits are 5/6 P = 1000¢ and 1/1 P = 1200¢. For pentatonic scales, the limits are 3/4 and 1/1, or 900-1200¢. Putting this all together:

Heptatonic second: 0-200¢

Heptatonic third: 300-400¢

Heptatonic fourth: 480-600¢

Heptatonic fifth: 600-720¢

Heptatonic sixth: 800-900¢

Heptatonic seventh: 1000-1200¢

Pentatonic second: 0-300¢

Pentatonic third: 400-600¢

Pentatonic fourth: 600-800¢

Pentatonic fifth: 900-1200¢

We see that there are gaps between the ranges. Some intervals like 7/6 can never be heptatonic generators because they fall through the cracks. Likewise some intervals can never be pentatonic generators. But every interval can be one or the other. What if N were 6 or 8?

Hexatonic second: 0-240¢

Hexatonic third, fourth and fifth: impossible, not co-prime

Hexatonic sixth: 960-1200¢

Octotonic second: 0-171¢ (171¢ = 1\7)

Octotonic third: impossible, not co-prime

Octotonic fourth: 400-480¢

Octotonic fifth: impossible, not co-prime

Octotonic sixth: 720-800¢

Octotonic seventh: impossible, not co-prime

Octotonic eighth: 1029-1200¢ (1029¢ = 6\7)

Look at all those gaps. 3/2 can never be a generator. It's obvious why hexatonic or octotonic notation is rarely used!

9-note second: 0-150¢

9-note third: 240-300¢

9-note fourth: impossible, not co-prime

9-note fifth: 515-600¢ (515¢ = 3\7)

9-note sixth: 600-685¢ (685¢ = 4\7)

9-note seventh: impossible, not co-prime

9-note eighth: 900-960¢

9-note ninth: 1050-1200¢

10-note second: 0-133¢ (133¢ = 1\9)

10-note third: impossible, not co-prime

10-note fourth: 343-400¢ (343¢ = 2\7)

10-note fifth, sixth and seventh: impossible, not co-prime

10-note eighth: 800-857¢ (857¢ = 5\7)

10-note ninth: impossible, not co-prime

10-note tenth: 1067-1200¢ (1067¢ = 2\9)

Again, many gaps, and the 3/2 can't be a generator. However the 9-note scale does fill in some gaps in the heptatonic range, and can be an alternative to pentatonicism.

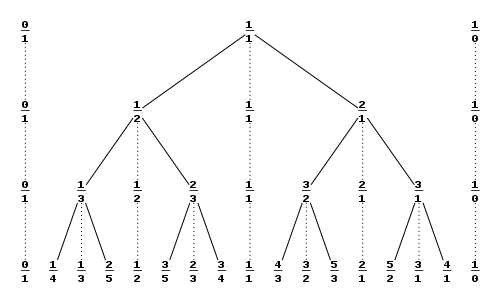
How to find X and Y? It helps if you know about the Stern-Brocot tree. Read about it here:

http://en.wikipedia.org/wiki/Stern%E2%80%93Brocot_tree

It turns out that the upper and lower limits of G/P are the ancestors of M/N on the Stern-Brocot tree! How do we know this? Because we know that X < N and Y < M. Therefore N - X < N and M - Y < M. So both limits have smaller numbers than M/N. And obviously the "freshman sum" of Y/X and (M - Y) / (N - X) is M/N. Furthermore, X and Y are relatively prime. If they weren't, suppose they were both even numbers, with X = 2V and Y = 2W. Then XM = YN + 1 becomes 2VM = 2WN + 1. But 2VM and 2WN are both even numbers, and an even number plus 1 must be an odd number. So X and Y can't both be even. By similar logic, they can't both be multiples of 3, or of 4, or of any other number. They must be co-prime.

How to find the ancestors of M/N? Suppose that G/P was exactly M/N. This would correspond to notating 7edo heptatonically. (By the way, G/P = M/N is the only way in which the final dotted line of the star can be a generator.) The generator is MP/N cents. The 2nd of the scale would be P/N cents. Now suppose we flatten that 2nd down to 0¢. That means X generators would be flattened down by P/N cents, and each generator would be flattened by P/(XN) cents. The original generator was G = MP/N, and the new generator would be G = MP/N - P/(XN) = P (XM - 1)/XN. The lower ancestor of M/N is therefore (XM - 1) / XN.

Similarly, the penultimate note is shy of the period by P/N cents. To close the gap, we must sharpen (N - X) generators by P/N cents, and sharpen one generator by P / [N(N - X)] cents. The new generator is G = MP/N + P / [N(N - X)] = P [(N - X)M + 1] / [(N - X)N]. The upper ancestor of M/N is therefore [(N - X)M + 1] / [(N - X)N]. Don't let this formula scare you. Once you find the lower ancestor, you can find the upper one by "freshman subtraction" of the lower one from M/N.

To find X, either consult the Stern-Brocot tree, or find X from the formula XM mod N = 1. If you find a number Z such that ZM mod N = -1, then X = N - Z.

EDO notation

Stern-Brocot ancestors have a specific application in notating EDOs.