Singtervals

Singtervals is a series of ear-training exercises originated by Andrew Heathwaite around 2011.

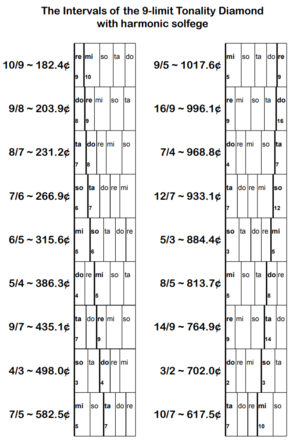
A rundown of 9-odd-limit Singtervals

The order of intervals as they correspond to the chart begin going down the left column, and back up from the bottom of the right column. This way, octave inversions of intervals are lined up next to one another.
Whenever the solfege appears, that is referring to a transposition of the harmonic series. do = 1/1, re = 9/8, mi = 5/4, so = 3/2, ta = 7/4.
The transpositions of do are by subharmonic intervals. (The subharmonic series is the harmonic series turned upside down i.e. 1/1, 1/2, 1/3, 1/4, etc.)
This is to facilitate changes of function of the 1/1. For example, in the first singterval, labeled 10/9, the tonic of the harmonic series is transposed to the 9th subharmonic, or 16/9, so that 1/1 functions as 9/8 (re) and 10/9 functions as 5/4 (mi).
This exercise is exhaustive of the 9-odd-limit, i.e. it contains every possible (octave-reduced) interval that can be expressed by a fraction between whole numbers 1 through 9.
The resulting intervals between the intervals being sung can be calculated by dividing the consecutive fractions. For example, the microtone between 10/9 and 9/8 is 81/80. Other intervals encountered include 64/63, 36/35, 25/24, 28/27, 21/20, and 49/48. Since all of these intervals are of the form (n + 1)/n, they fall within the category of superparticular intervals.
A handy way to convert a ratio a/b to cents is to Google log(a/b)/log(2)*1200. For example, typing log(10/9)/log(2)*1200 into Google yields 182.403712134!