Fokker block
| This is a beginner page. It is written to allow new readers to learn about the basics of the topic easily. The corresponding expert page for this topic is Mathematical theory of Fokker blocks. |
A Fokker block (or periodicity block) is a periodic scale that can be thought of as a tile on a lattice of pitch classes (of a JI subgroup or a regular temperament) shaped as a parallelogram, parallelepiped or higher-dimensional analog. It comprises those intervals in the lattice which fall inside the tile after moving the tile on the lattice to a place where no lattice point is on its boundary. (Different positions of the tile can create scales which are not rotations of each other.) The scale repeats at the interval of equivalence, which lies on the unison in the lattice of pitch classes.
All Fokker blocks are weakly epimorphic, which means that there is a val that maps each note of the Fokker block onto its own equal temperament scale step and leaves no equal temperament scale step without a mapping towards it. (In other words, this val provides a bijection between the Fokker block and the equal temperament.) If a Fokker block is epimorphic, which means that the val preserves the order of the steps, it is a strong Fokker block; otherwise it is a weak Fokker block. The expression "Fokker block" without any qualifier generally denotes a strong block.
The concept of the Fokker block was developed by the physicist and music theorist Adriaan Fokker.
Theory
Fokker blocks have a shape which tiles the lattice; an interval between pitches which lie across an edge of two Fokker blocks within the tiling will be altered from its normal value by an interval corresponding to an edge of the parellelepiped. This edge turns out to be the difference between intervals that span the same number of steps in the scale, and so it is called a chroma. (Fokker called them unison vectors in his original text.)
If we place the coordinate vectors of the chromas into a matrix, the number of notes in the Fokker block is equal to the determinant of that matrix. It is also equal to the volume of the parallelepiped formed by the chromas, which is called the fundamental domain.
The rank of a Fokker block is the rank of the underlying lattice of pitches including the interval of equivalence. A rank-n Fokker block has n - 1 chromas: a consequence of this is that a Fokker block of rank n has maximum variety at most 2(n − 1) (since that's the number of combinations of chromas a note can be altered by). For example, a rank-2 Fokker block has max variety at most 2 (hence is a mos), and a rank-3 Fokker block has max variety at most 4. These results are true for strong and weak Fokker blocks only if we allow negative steps; otherwise they are only true for strong Fokker blocks. In this way, Fokker blocks generalize mos scales.
A Fokker block can be made constant structure (with negative steps allowed) by moving the generator sizes by an arbitrarily small amount. If the logarithmic sizes of the generators are linearly independent (as happens in JI, for example), the generator sizes need not be moved. The constant structure will have no negative steps if and only if the Fokker block is strong.
A Fokker arena contains all the periodic scales that can be constructed as Fokker blocks from the same list of chromas.
Examples
Ptolemy's intense diatonic
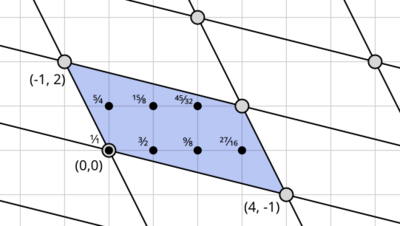
Let's take 5-limit just intonation, and pick the just chromatic semitone (25/24) and the syntonic comma (81/80) as our chromas.
The octave equivalent lattice is generated by fifths and just major thirds. Since [math]\displaystyle{ 25/24 = 2^{-3} \cdot 3^{-1} \cdot 5^2 }[/math], it has coordinates [math]\displaystyle{ (-1, 2) }[/math] in the octave-equivalent lattice. The syntonic comma is reached by stacking 4 fifths and going down a major third, so it has coordinates [math]\displaystyle{ (4, -1) }[/math].
The corresponding Fokker block is Ptolemy's intense diatonic, also known as Zarlino, specifically the lydian mode.
Tempering out either of the two chromas gives a MOS scale related to the temperament.
- Tempering out the syntonic comma gives the diatonic scale LLLsLLs, in meantone.
- Tempering out the chromatic semitone gives the mosh LsLsLss (a 7-note neutral scale), in dicot.
If we temper out both 25/24 and 81/80, we get 7 equal temperament, which we can interpret as an equalized diatonic scale. This scale is a Fokker block in multiple ways: it is also possible to arrive at the same set of notes using 135/128 together with either 81/80 or 25/24 as the chromas.
Duodene and 12 equal temperament
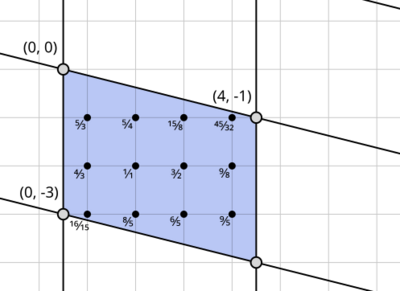
Let's now use the diesis (128/125) and the syntonic comma (81/80) as our chromas, in 5-limit JI as above.
The diesis is the difference between an octave and three major thirds, so it has coordinates [math]\displaystyle{ (0, -3) }[/math].
The number of notes in the tile will be 12, since the determinant is:
- [math]\displaystyle{ \begin{vmatrix} 0 & -3 \\ 4 & -1 \end{vmatrix} = (0 \cdot -1) - (-3 \cdot 4) = 12 }[/math]
This should not be surprising, as 12 equal temperament tempers out exactly these two commas, so each note in the resulting scale will correspond to an interval of 12et. The resulting just scale is known as duodene.
See also
- This Python code can be used to find Fokker blocks.
- Catalog of Fokker blocks
- List of weak Fokker blocks
- Fokker chord
- Minkowski block
- Minkowski reduced bases for Fokker groups of certain vals
