N2D3P9
N2D3P9 (Entoo-Deethree-Peenine) is a mathematical function which was developed to help in designing the Sagittal microtonal notation. Given a rational number [math]\frac{n}{d}[/math] representing a pitch (relative to some tonic note), N2D3P9 estimates its rank in popularity among all rational pitches in musical use. A low value of N2D3P9 indicates that the ratio is used often, and so should have a simple accidental symbol, while a high value indicates that the ratio is used rarely and so can have a more complex symbol if necessary. It may also be useful in designing rational scales or tunings. The name "N2D3P9" is an abbreviation of key components of its formula, as described below.
As a mnemonic, you can imagine the name N2D3P9 comes from a fictional character in the Star Wars franchise. In an alternative timeline, the young Anakin Skywalker assembles the droid N2D3P9 from the parts of three other droids: R2D2, C3P0 and NR-N99.
Formula
Before describing how to calculate [math]\text{N2D3P9}[/math], we define three simpler terms that are used in its formula:
- 2,3-free ratios, which are also known as "5-rough" ratios. Because factors of [math]2[/math] and [math]3[/math] in pitch ratios are already notated by changing octaves or moving along the chain of fifths (... B♭♭ F♭ C♭ G♭ D♭ A♭ E♭ B♭ F C G D A E B F♯ C♯ G♯ D♯ A♯ E♯ B♯ Fx ...), N2D3P9 only operates on ratios that have had their factors of [math]2[/math] and [math]3[/math] removed. For example, there are various numbers of factors of [math]2[/math] and [math]3[/math] in the following ratios: [math]\frac{16}{15}, \frac{10}{9}, \frac{6}{5}, \frac{5}{4}, \frac{27}{20}, \frac{45}{32}, \frac{64}{45}, \frac{40}{27}, \frac{8}{5}, \frac{5}{3}, \frac{9}{5}, \frac{15}{8}[/math], but when their factors of [math]2[/math] and [math]3[/math] are removed, they all reduce to [math]\frac{1}{5}[/math] or [math]\frac{5}{1}[/math], and so they can all be notated using the same microtonal accidental, pointing either up or down, combined with different letters and sharps or flats. We say that [math]\frac{1}{5}[/math] or [math]\frac{5}{1}[/math] is the 2,3-removed or 2,3-free form of these pitch ratios, and because [math]\frac{1}{5}[/math] and [math]\frac{5}{1}[/math] use the same accidental pointing either up or down, and because N2D3P9 only operates on ratios whose numerator is larger than their denominator (superunison ratios), [math]\frac{5}{1}[/math] can represent this entire 2,3-equivalent pitch ratio class or 2,3-equivalence-class for the purpose of notation design.
- The copfr function, which stands for "Count Of Prime Factors with Repeats". It applies to any positive integer. For example [math]175[/math] has the prime factorization [math]5 × 5 × 7[/math], which has 3 factors including the repeat of [math]5[/math], so [math]\text{copfr}(175) = 3[/math]. [math]\text{copfr}(1) = 0[/math]. [math]\text{copfr}[/math] is also called the "big omega" function, [math]Ω[/math].
- The prime-limit function, which is also known as [math]\text{gpf}[/math], which stands for greatest prime factor. [math]\text{prime-limit}(175) = 7[/math]. Some authors leave [math]\text{prime-limit}(1)[/math] undefined; we avoid the question because we define [math]\text{N2D3P9}(\frac{1}{1})[/math] ≡ [math]\text{N2D3P9}(\frac{3}{1}) = 1[/math]. This is because the ratios in the equivalence class represented by the 2,3-removed [math]\frac{1}{1}[/math] actually have a prime limit of 3.
Now we can give the formula for [math]\text{N2D3P9}[/math]([math]\frac{n}{d}[/math]) as: $$ \begin{cases} \large{\text{N2D3P9}(\frac{n}{d})=\frac{n}{2^{\text{copfr}(n)}}×\frac{d}{3^{\text{copfr}(d)}}×\frac{\text{prime-limit}(nd)}{9}}, \\ \small{\text{ where }n\text{ and }d\text{ are 2,3-free positive integers and }n>d.} \\ \large{\text{N2D3P9}(\frac{1}{1})=1} \\ \end{cases} $$ Note that where
[math]n = 5^{n_5}×7^{n_7}×11^{n_{11}}×...[/math]
we have
[math]2^{\text{copfr}(n)}=2^{n_5}×2^{n_7}×2^{n_{11}}×...[/math]
and so
[math]\frac{n}{2^{\text{copfr}(n)}}=(\frac{5}{2})^{n_5}×(\frac{7}{2})^{n_7}×(\frac{11}{2})^{n_{11}}×...[/math]
and similarly
[math]\frac{d}{3^{\text{copfr}(d)}}=(\frac{5}{3})^{d_5}×(\frac{7}{3})^{d_7}×(\frac{11}{3})^{d_{11}}×...[/math]
These can be described respectively as "product of half prime factors of the numerator (with repeats)" and "product of one-third prime factors of the denominator (with repeats)". So we can describe the procedure for calculating [math]\text{N2D3P9}[/math]([math]\frac{n}{d}[/math]) as:
Take the prime factorization of the numerator and divide all the primes by 2, then multiply it out again. Do the same with the denominator but divide the primes by 3 instead of 2. Multiply these two results together then multiply by the prime limit of the ratio and divide by 9.
[math]\text{N2D3P9}[/math] can also be written as: $$\text{N2D3P9}(\frac{n}{d})=\frac{nd⋅\text{gpf}(nd)}{2^{Ω(n)}3^{Ω(d) + 2}} $$ where [math]nd[/math] is established in music theory as a ratio's "product complexity" or Benedetti height.
The division by 9 does not affect the ranking, but it has the convenient effect that [math]\text{N2D3P9}[/math] values are almost the same as the ranks they produce when applied to all 2,3-free superunison ratios. Putting it another way, there are approximately [math]N[/math] 2,3-free pitch ratios with [math]\text{N2D3P9}≤N[/math]. For example, [math]\text{N2D3P9}(\frac{77}{5}) = \frac{7}{2} × \frac{11}{2} × \frac{5}{3} × \frac{11}{9} ≈ 39[/math], suggesting there are approximately 38 other 2,3-free pitch ratios more popular than [math]\frac{77}{5}[/math]. There are actually about 4% fewer than that on average. In this case there are 36.
Justification
Why should we believe that [math]\text{N2D3P9}[/math] accurately ranks the popularity of 2,3-equivalent pitch classes?
[math]\text{N2D3P9}[/math] was developed (or discovered) rather late in the development of Sagittal notation. The Sagittal designers previously relied on actual ratio usage data from the Huygens-Fokker Foundation's scale archive, kindly provided by Manuel Op de Coul.
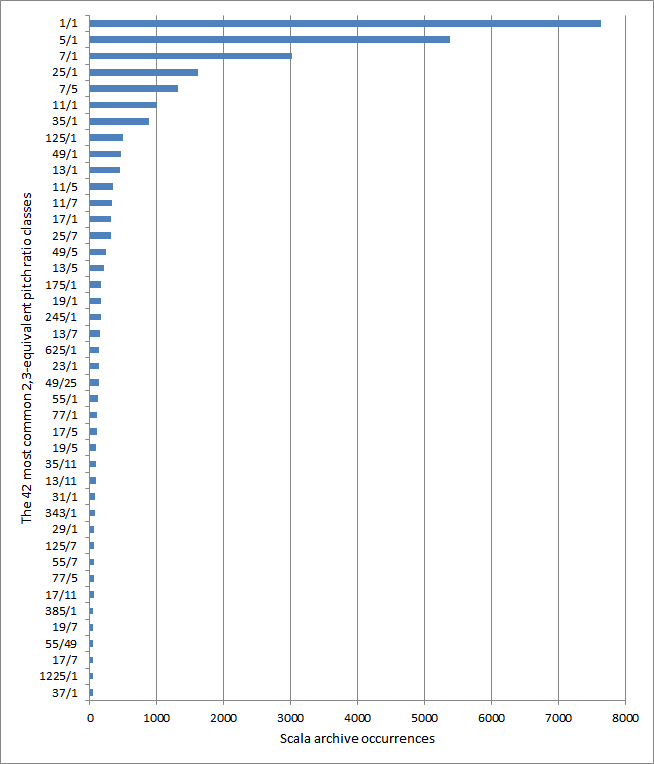
All scales in the archive were treated equally, as there was no information about their relative importance. Each occurrence of a pitch ratio in a scale was counted as one vote for that ratio. Then the ratios were grouped into 2,3-equivalent pitch classes and a single figure obtained for each 2,3-free superunison ratio (representing the class). There were 29,403 votes, allocated to 820 2,3-free ratios.
Like the frequency of use of letters in an alphabet, when sorted in order of decreasing popularity, the ratios obeyed an approximate Zipf's law distribution, with the Nth most popular ratio having votes proportional to approximately [math]\frac{1}{N^{1.37}}[/math]. This meant that about half the ratios had only one vote each, and three quarters of them had 3 votes or less. Such low numbers of votes meant that the data on the less popular ratios was vulnerable to "historical noise". In other words, the position of such a ratio in the list might not be a good predictor of its relative frequency of use in the future.
In the early stages of Sagittal design, when allocating symbols for the most popular ratios, the designers could rely on the Scala archive data, but when they moved on to less popular ratios they needed some "less noisy" way to rank them.
Blumeyer and Keenan found that [math]\text{N2D3P9}[/math] is a psychoacoustically plausible function of a ratio's prime factorization that:
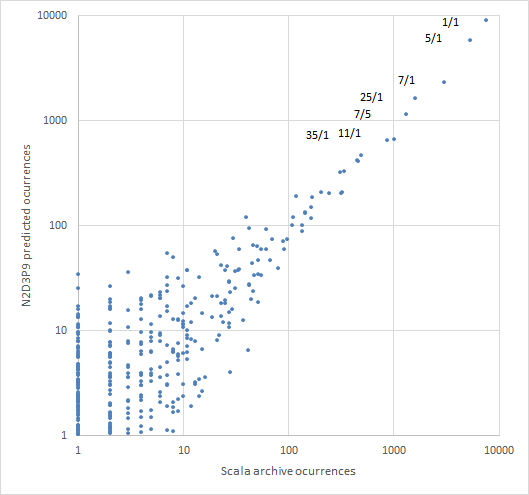
- ranks 10 of the 11 most popular ratio classes in exactly the same way as the archive data, and
- ranks all 820 ratio classes in a way that has a low sum of squared errors in their ranks, relative to the archive data, and
- is sufficiently simple, having only two parameters, that it cannot be overfitting the data, and should therefore serve to average out the historical noise in the ranking of the less popular ratios, including ratios that do not occur in the archive at all.
However, their approach was not able to consider all possible psychoacoustic reasons for a ratio's popularity. For example, [math]\text{N2D3P9}[/math] does not evaluate whether some member of a 2,3-equivalence-class might be very close in pitch to some member of another 2,3-equivalence-class, such as [math]\frac{65}{64}[/math] being very close to [math]\frac{1}{1}[/math].
Development/discovery
From May to August 2020, a collaborative effort to find such a function, was carried out by members of the Sagittal forum, led by Sagittal co-creator Dave Keenan and Douglas Blumeyer. Many functions besides [math]\text{N2D3P9}[/math] were considered before selecting it as the best function for its purpose.
Estimation of pitch ratio popularity is possible because it correlates with numeric simplicity. [math]\text{N2D3P9}[/math] is most useful when comparing ranks of more complex ratios, because usage data about such ratios is sparse. By fitting a function to the statistical usage data which is available for simpler ratios, [math]\text{N2D3P9}[/math] enables the extension of the patterns found in these simpler ratios.
Rather than attempt to fit functions to the exact counts of votes for each ratio, the functions were fit to the rank indices of each ratio; in other words, a function only needed to sort ratios the same as the actual data, and within each rank position it was unimportant how close its estimate of votes was. In technical parlance, the goal was to maximize the Spearman’s rank coefficient between the estimated ranks and the actual ranks. For purposes of comparing competing functions, maximizing Spearman’s rank coefficient could be simplified to minimizing the sum of squared differences between the ranks. But because fitting to the simpler ratios which had more votes is more important, a Zipf's-law weighting was applied to the ranks by taking their reciprocals before calculating their squared differences. A fractional ranking strategy was used to ensure that stretches of the data with tied vote counts did not distort the measurement.
The overall strategy, then, was to minimize this weighted rank error, while also minimizing the complexity of the function, to avoid overfitting. An earlier notational popularity ranking function for 2,3-removed-ratios, that had been used by the creators of Sagittal was [math]\text{sopfr}[/math] (sum of prime factors with repetition). It does a remarkably good job of estimating the rank of pitch ratios given how simple it is. However the weighted sum of squared errors that [math]\text{sopfr}[/math] gives for the Scala stats is about 0.026, while [math]\text{N2D3P9}[/math] reduces that to about 0.010. Functions giving sums of squares as low as 0.008 were found, however, these functions were so complex that they probably were fitting to noise in the Scala stats instead of to the true nature of musical pitch. An informal “chunk” metric was devised to compare function complexity in terms of ability to fit to the data, with considered functions ranging from one chunk ([math]\text{sopfr}[/math]) to eight chunks; the winning function [math]\text{N2D3P9}[/math] has five chunks.
Several techniques were used to find and decide on [math]\text{N2D3P9}[/math] as the best 2,3-removed-ratio notational-popularity rank-estimation function. Initial observations about shortcomings of [math]\text{sopfr}[/math], such as its failure to differentiate balanced ratios from their imbalanced equivalents — such as [math]\frac{11}{5}[/math] versus [math]\frac{55}{1}[/math] — or those with different prime limits such as [math]\frac{13}{5}[/math] and [math]\frac{11}{7}[/math], despite those pairs of ratios exhibiting remarkably different actual ranks in the Scala stats, formed the basis of the investigation. Psychoacoustic plausibility of functions was used as a top-down guide for experimentation. Optimization tools such as Excel's Evolutionary Solver were used to navigate toward ideal values for each parameter. The approach that was finally successful was a brute-force approach implemented by Douglas Blumeyer, whereby nearly 2 billion functions combined out of constituent "submetrics" were checked automatically. In the end, one of the functions on the short-list generated from the brute-force checker was recognized as being re-writable in a much simpler form with parameter values rounded to whole numbers without doing much damage to its sum-of-squares, and thus [math]\text{N2D3P9}[/math] was born.
After deciding upon [math]\text{N2D3P9}[/math], the Sagittal forum members checked the ratios for the existing Sagittal symbols against it, to see how well they'd been served by the Scala archive stats and the earlier [math]\text{sopfr}[/math] metric. Each symbol in Sagittal's JI notations has a default value, or primary comma, which for our purposes is a rational number between 1 and sqrt(3¹⁹/2³⁰) ≈ 1.040404 exclusive, that by multiplication, takes us from some 3-smooth ratio (notated using standard music notation) to a nearby 5-rough ratio. This allows the symbol to exactly notate all the ratios in the corresponding 2,3-equivalence-class. For example, the most important such comma is 81/80 (the 1/5-comma), whose symbol is an upward pointing left-half-arrow ⁄|, which takes us from 2⁴/3⁴ (A♭) to 1/5 (A♭ ⁄|). Based on N2D3P9, it was found that only a couple of these commas should be changed (these were among the rarest-used symbols in Sagittal). This was as expected; [math]\text{N2D3P9}[/math] was developed primarily in order to add new accent marks to Sagittal, to enable it to exactly notate even rarer JI pitches than it already does.
Table of top 100 (2,3-equivalent) pitch ratio classes by N2D3P9
| 2,3-equivalent pitch ratio class | N2D3P9 | N2D3P9 rank | Scala archive rank | Scala archive occurrences |
|---|---|---|---|---|
| {1}₂,₃ | 1 | 1 | 1 | 7624 |
| {5}₂,₃ | 1.39 | 2 | 2 | 5371 |
| {7}₂,₃ | 2.72 | 3 | 3 | 3016 |
| {25}₂,₃ | 3.47 | 4 | 4 | 1610 |
| {7/5}₂,₃ | 4.54 | 5 | 5 | 1318 |
| {11}₂,₃ | 6.72 | 6 | 6 | 1002 |
| {35}₂,₃ | 6.81 | 7 | 7 | 875 |
| {125}₂,₃ | 8.68 | 8 | 8 | 492 |
| {13}₂,₃ | 9.39 | 9 | 10 | 447 |
| {49}₂,₃ | 9.53 | 10 | 9 | 463 |
| {11/5}₂,₃ | 11.2 | 11 | 11 | 339 |
| {25/7}₂,₃ | 11.34 | 12 | 14 | 312 |
| {13/5}₂,₃ | 15.65 | 13 | 16 | 205 |
| {11/7}₂,₃ | 15.69 | 14 | 12 | 324 |
| {49/5}₂,₃ | 15.88 | 15 | 15 | 246 |
| {17}₂,₃ | 16.06 | 16 | 13 | 318 |
| {55}₂,₃ | 16.81 | 17 | 24 | 119 |
| {175}₂,₃ | 17.01 | 18 | 17 | 168 |
| {19}₂,₃ | 20.06 | 19 | 18 | 166 |
| {625}₂,₃ | 21.7 | 20 | 21 | 143 |
| {13/7}₂,₃ | 21.91 | 21 | 20 | 145 |
| {65}₂,₃ | 23.47 | 22 | 50 | 40 |
| {77}₂,₃ | 23.53 | 23 | 25 | 111 |
| {245}₂,₃ | 23.82 | 24 | 19 | 165 |
| {49/25}₂,₃ | 26.47 | 25 | 23 | 134 |
| {17/5}₂,₃ | 26.76 | 26 | 26 | 108 |
| {25/11}₂,₃ | 28.01 | 27 | 47 | 42 |
| {125/7}₂,₃ | 28.36 | 28 | 33 | 62 |
| {23}₂,₃ | 29.39 | 29 | 22 | 136 |
| {91}₂,₃ | 32.86 | 30 | 57 | 30 |
| {343}₂,₃ | 33.35 | 31 | 31 | 70 |
| {19/5}₂,₃ | 33.43 | 32 | 27 | 97 |
| {13/11}₂,₃ | 34.43 | 33 | 29 | 89 |
| {121}₂,₃ | 36.97 | 34 | 42.5 | 46 |
| {17/7}₂,₃ | 37.46 | 35 | 40 | 50 |
| {25/13}₂,₃ | 39.12 | 36 | 52.5 | 34 |
| {77/5}₂,₃ | 39.21 | 38 | 28 | 92 |
| {55/7}₂,₃ | 39.21 | 38 | 34 | 61 |
| {35/11}₂,₃ | 39.21 | 38 | 35.5 | 55 |
| {85}₂,₃ | 40.14 | 40 | 78 | 20 |
| {275}₂,₃ | 42.01 | 41 | 147 | 7 |
| {875}₂,₃ | 42.53 | 42 | 76 | 21 |
| {29}₂,₃ | 46.72 | 43 | 32 | 67 |
| {19/7}₂,₃ | 46.8 | 44 | 37.5 | 52 |
| {23/5}₂,₃ | 48.98 | 45 | 44 | 45 |
| {95}₂,₃ | 50.14 | 46 | 72 | 23 |
| {143}₂,₃ | 51.64 | 47 | 66 | 26 |
| {31}₂,₃ | 53.39 | 48 | 30 | 80 |
| {3125}₂,₃ | 54.25 | 49 | 52.5 | 34 |
| {91/5}₂,₃ | 54.77 | 51 | 68 | 25 |
| {65/7}₂,₃ | 54.77 | 51 | 102.5 | 11 |
| {35/13}₂,₃ | 54.77 | 51 | 102.5 | 11 |
| {49/11}₂,₃ | 54.9 | 53 | 54 | 33 |
| {343/5}₂,₃ | 55.58 | 54 | 55.5 | 31 |
| {119}₂,₃ | 56.19 | 55 | 252.5 | 3 |
| {325}₂,₃ | 58.68 | 56 | 604.5 | 1 |
| {385}₂,₃ | 58.82 | 57 | 37.5 | 52 |
| {17/11}₂,₃ | 58.87 | 58 | 35.5 | 55 |
| {1225}₂,₃ | 59.55 | 59 | 41 | 47 |
| {169}₂,₃ | 61.03 | 60 | 86 | 14 |
| {121/5}₂,₃ | 61.62 | 61 | 147 | 7 |
| {77/25}₂,₃ | 65.35 | 62 | 63 | 27 |
| {125/49}₂,₃ | 66.17 | 63 | 63 | 27 |
| {25/17}₂,₃ | 66.9 | 64 | 134.5 | 8 |
| {23/7}₂,₃ | 68.57 | 65 | 47 | 42 |
| {17/13}₂,₃ | 69.57 | 66 | 47 | 42 |
| {125/11}₂,₃ | 70.02 | 67 | 147 | 7 |
| {133}₂,₃ | 70.19 | 68 | 329 | 2 |
| {625/7}₂,₃ | 70.89 | 69 | 113 | 10 |
| {115}₂,₃ | 73.47 | 70 | 604.5 | 1 |
| {19/11}₂,₃ | 73.54 | 71 | 55.5 | 31 |
| {37}₂,₃ | 76.06 | 72 | 42.5 | 46 |
| {49/13}₂,₃ | 76.68 | 73 | 147 | 7 |
| {29/5}₂,₃ | 77.87 | 74 | 59.5 | 28 |
| {455}₂,₃ | 82.15 | 75 | 186.5 | 5 |
| {539}₂,₃ | 82.35 | 76 | 186.5 | 5 |
| {1715}₂,₃ | 83.37 | 77 | 76 | 21 |
| {25/19}₂,₃ | 83.56 | 78 | 79.5 | 19 |
| {143/5}₂,₃ | 86.06 | 80 | 217.5 | 4 |
| {65/11}₂,₃ | 86.06 | 80 | 164 | 6 |
| {55/13}₂,₃ | 86.06 | 80 | 90 | 13 |
| {121/7}₂,₃ | 86.27 | 82 | 164 | 6 |
| {19/13}₂,₃ | 86.91 | 83 | 45 | 44 |
| {187}₂,₃ | 88.31 | 84 | 217.5 | 4 |
| {31/5}₂,₃ | 88.98 | 85 | 68 | 25 |
| {91/25}₂,₃ | 91.28 | 86 | 329 | 2 |
| {55/49}₂,₃ | 91.5 | 87 | 39 | 51 |
| {605}₂,₃ | 92.43 | 88 | 94.5 | 12 |
| {343/25}₂,₃ | 92.63 | 89 | 68 | 25 |
| {41}₂,₃ | 93.39 | 90 | 72 | 23 |
| {119/5}₂,₃ | 93.66 | 92 | 123.5 | 9 |
| {85/7}₂,₃ | 93.66 | 92 | - | 0 |
| {35/17}₂,₃ | 93.66 | 92 | 217.5 | 4 |
| {125/13}₂,₃ | 97.8 | 94 | 604.5 | 1 |
| {275/7}₂,₃ | 98.03 | 95.5 | 102.5 | 11 |
| {175/11}₂,₃ | 98.03 | 95.5 | 147 | 7 |
| {425}₂,₃ | 100.35 | 97 | 329 | 2 |
| {169/5}₂,₃ | 101.71 | 98 | 329 | 2 |
| {121/25}₂,₃ | 102.7 | 99 | 217.5 | 4 |
| {43}₂,₃ | 102.72 | 100 | 58 | 29 |
See also
Keenan, D., Blumeyer, D. (2022). N2D3P9. In: Montiel, M., Agustín-Aquino, O.A., Gómez, F., Kastine, J., Lluis-Puebla, E., Milam, B. (eds) Mathematics and Computation in Music. MCM 2022. Lecture Notes in Computer Science(), vol 13267. Springer, Cham.