Moving the bridge hack
If you have a 12edo guitar, or other fretted string instrument, and you want to play in an EDO that is numerically near 12 (e.g. 11edo or 13edo), then rather than redoing the whole fretboard, you might be tempted simply to move the bridge. If you move the bridge so that the 13th fret is now precisely 2/1, the frets will play precisely 13edo, right?
...well, actually, no. The frets form a geometric series of lengths that converges at a specific point, which is where the bridge ought to be. (That's what an EDO is—a geometric sequence of frequencies, corresponding to a geometric sequence of string lengths.) If you move the bridge, the new string lengths no longer form a mathematically correct geometric sequence. However, depending on what range of the fretboard you want to be usable, and what accuracy you desire, a moving-the-bridge solution may be possible.
Derivation of the resulting scale
Let the EDO number of the original instrument be N (so very often N = 12). Let the original scale length of the instrument (distance from bridge to nut) be 1. In other words we're measuring all lengths relative to the original scale length. Then the playable string lengths of the unmodified instrument are
[math]\displaystyle{ 2^{-i/N} \text{ for } i = 0, 1, 2, 3\dots }[/math]
If the bridge is moved so that the new scale length is x, this adds (x − 1) to all string lengths, so the new string lengths are simply
[math]\displaystyle{ 2^{-i/N} + x - 1 \text{ for } i = 0, 1, 2, 3\dots }[/math]
The frequencies are inversely proportional to the string lengths. If we plug in i = 0 to the above formula, we get x, so the frequency ratios relative to the open string are
[math]\displaystyle{ \frac{x}{2^{-i/N} + x - 1} \text{ for } i = 0, 1, 2, 3\dots }[/math]
Converting those frequency ratios into cents in the usual way (taking the log to base 2 and multiplying by 1200) gives the new scale in cents.
Each fret will raise the pitch by a different amount, as these charts show
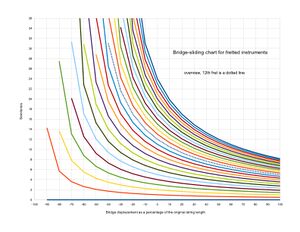
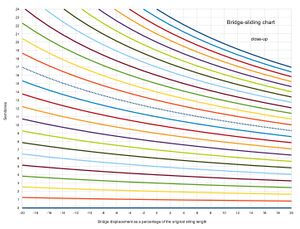
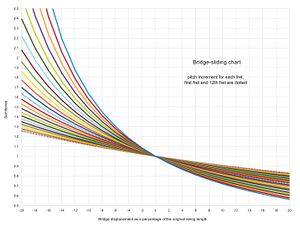
Examples for converting a 12edo instrument
9edo
The naive way to position the bridge for 9edo would be to make the 9th fret play an exact 2/1. However, this causes a rather large amount of error in some lower frets (as well as, of course, the higher ones above fret 9):
| Fret number | Cents | Deviation from 9edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 124.191 | −9.142 |
| 2 | 250.196 | −16.471 |
| 3 | 378.179 | −21.821 |
| 4 | 508.328 | −25.005 |
| 5 | 640.854 | −25.813 |
| 6 | 775.993 | −24.007 |
| 7 | 914.017 | −19.317 |
| 8 | 1055.234 | −11.433 |
| 9 | 1200.000 | 0.000 |
| 10 | 1348.726 | 15.392 |
| 11 | 1501.890 | 35.223 |
| 12 | 1660.056 | 60.056 |
| 13 | 1823.890 | 90.557 |
Can the error be reduced? Yes, at the expense of having a smaller usable range of fretboard. For example, let's say we want to limit the maximum error to 10 cents. How many frets can we use at this level of accuracy?
| Fret number | Cents | Deviation from 9edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 127.785 | −5.548 |
| 2 | 257.717 | −8.950 |
| 3 | 390.004 | −9.996 |
| 4 | 524.880 | −8.453 |
| 5 | 662.614 | −4.053 |
| 6 | 803.509 | 3.509 |
| 7 | 947.916 | 14.583 |
| 8 | 1096.241 | 29.574 |
| 9 | 1248.955 | 48.955 |
The answer is six frets. (It's impossible to make the seventh fret more accurate without the error of the third fret exceeding 10 cents.) Perhaps surprisingly, this level of accuracy for the first six frets is only achievable by making the 9th fret at least 1249 cents, rather than 2/1.
10edo
Pure 2/1:
| Fret number | Cents | Deviation from 10edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 114.426 | −5.574 |
| 2 | 229.842 | −10.158 |
| 3 | 346.326 | −13.674 |
| 4 | 463.963 | −16.037 |
| 5 | 582.847 | −17.153 |
| 6 | 703.082 | −16.918 |
| 7 | 824.780 | −15.220 |
| 8 | 948.070 | −11.930 |
| 9 | 1073.091 | −6.909 |
| 10 | 1200.000 | 0.000 |
| 11 | 1328.973 | 8.973 |
| 12 | 1460.208 | 20.208 |
| 13 | 1593.926 | 33.926 |
| 14 | 1730.381 | 50.381 |
| 15 | 1869.859 | 69.859 |
Max error limited to 10 cents (only the first 9 frets may be used):
| Fret number | Cents | Deviation from 10edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 115.766 | −4.234 |
| 2 | 232.628 | −7.372 |
| 3 | 350.674 | −9.326 |
| 4 | 470.000 | −10.000 |
| 5 | 590.714 | −9.286 |
| 6 | 712.933 | −7.067 |
| 7 | 836.788 | −3.212 |
| 8 | 962.426 | 2.426 |
| 9 | 1090.010 | 10.010 |
| 10 | 1219.720 | 19.720 |
| 11 | 1351.764 | 31.764 |
| 12 | 1486.373 | 46.373 |
| 13 | 1623.811 | 63.811 |
11edo
Pure 2/1:
| Fret number | Cents | Deviation from 11edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 106.521 | −2.570 |
| 2 | 213.456 | −4.726 |
| 3 | 320.834 | −6.439 |
| 4 | 428.685 | −7.678 |
| 5 | 537.043 | −8.412 |
| 6 | 645.941 | −8.604 |
| 7 | 755.419 | −8.218 |
| 8 | 865.517 | −7.210 |
| 9 | 976.280 | −5.538 |
| 10 | 1087.757 | −3.152 |
| 11 | 1200.000 | 0.000 |
| 12 | 1313.066 | 3.975 |
| 13 | 1427.017 | 8.836 |
| 14 | 1541.922 | 14.649 |
| 15 | 1657.854 | 21.491 |
| 16 | 1774.895 | 29.441 |
| 17 | 1893.135 | 38.589 |
| 18 | 2012.670 | 49.034 |
| 19 | 2133.611 | 60.884 |
Super-accurate, error limited to 1 cent (only the first 4 frets may be used):
| Fret number | Cents | Deviation from 11edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 108.322 | −0.769 |
| 2 | 217.183 | −0.998 |
| 3 | 326.621 | −0.652 |
| 4 | 436.676 | 0.313 |
| 5 | 547.394 | 1.939 |
| 6 | 658.821 | 4.276 |
13edo
Pure 2/1:
| Fret number | Cents | Deviation from 13edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 94.538 | 2.230 |
| 2 | 188.770 | 4.154 |
| 3 | 282.679 | 5.756 |
| 4 | 376.250 | 7.019 |
| 5 | 469.465 | 7.926 |
| 6 | 562.305 | 8.458 |
| 7 | 654.751 | 8.597 |
| 8 | 746.784 | 8.322 |
| 9 | 838.383 | 7.613 |
| 10 | 929.526 | 6.449 |
| 11 | 1020.193 | 4.808 |
| 12 | 1110.358 | 2.666 |
| 13 | 1200.000 | 0.000 |
| 14 | 1289.093 | −3.215 |
| 15 | 1377.612 | −7.004 |
| 16 | 1465.530 | −11.393 |
| 17 | 1552.822 | −16.409 |
| 18 | 1639.458 | −22.080 |
| 19 | 1725.412 | −28.434 |
| 20 | 1810.654 | −35.500 |
| 21 | 1895.155 | −43.307 |
| 22 | 1978.883 | −51.886 |
| 23 | 2061.810 | −61.267 |
Super-accurate, error limited to 1 cent (only the first 5 frets may be used):
| Fret number | Cents | Deviation from 13edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 93.001 | 0.693 |
| 2 | 185.616 | 1.000 |
| 3 | 277.826 | 0.903 |
| 4 | 369.611 | 0.380 |
| 5 | 460.950 | −0.588 |
| 6 | 551.821 | −2.025 |
| 7 | 642.202 | −3.952 |
14edo
Pure 2/1:
| Fret number | Cents | Deviation from 14edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 89.903 | 4.189 |
| 2 | 179.269 | 7.841 |
| 3 | 268.074 | 10.931 |
| 4 | 356.292 | 13.435 |
| 5 | 443.896 | 15.324 |
| 6 | 530.859 | 16.573 |
| 7 | 617.153 | 17.153 |
| 8 | 702.749 | 17.035 |
| 9 | 787.619 | 16.190 |
| 10 | 871.731 | 14.588 |
| 11 | 955.057 | 12.200 |
| 12 | 1037.564 | 8.993 |
| 13 | 1119.223 | 4.937 |
| 14 | 1200.000 | 0.000 |
| 15 | 1279.864 | −5.850 |
| 16 | 1358.784 | −12.645 |
| 17 | 1436.727 | −20.416 |
| 18 | 1513.660 | −29.197 |
| 19 | 1589.553 | −39.019 |
| 20 | 1664.373 | −49.913 |
| 21 | 1738.090 | −61.910 |
Max error limited to 10 cents (only the first 12 frets may be used):
| Fret number | Cents | Deviation from 14edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 88.925 | 3.210 |
| 2 | 177.267 | 5.839 |
| 3 | 265.002 | 7.859 |
| 4 | 352.101 | 9.244 |
| 5 | 438.538 | 9.966 |
| 6 | 524.283 | 9.997 |
| 7 | 609.307 | 9.307 |
| 8 | 693.580 | 7.866 |
| 9 | 777.073 | 5.645 |
| 10 | 859.755 | 2.612 |
| 11 | 941.593 | −1.264 |
| 12 | 1022.558 | −6.014 |
| 13 | 1102.616 | −11.670 |
| 14 | 1181.736 | −18.264 |
| 15 | 1259.886 | −25.829 |
| 16 | 1337.033 | −34.395 |
| 17 | 1413.146 | −43.996 |
| 18 | 1488.194 | −54.663 |
| 19 | 1562.144 | −66.427 |
15edo
Pure 2/1:
| Fret number | Cents | Deviation from 15edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 85.927 | 5.927 |
| 2 | 171.140 | 11.140 |
| 3 | 255.611 | 15.611 |
| 4 | 339.310 | 19.310 |
| 5 | 422.204 | 22.204 |
| 6 | 504.264 | 24.264 |
| 7 | 585.458 | 25.458 |
| 8 | 665.754 | 25.754 |
| 9 | 745.120 | 25.120 |
| 10 | 823.524 | 23.524 |
| 11 | 900.935 | 20.935 |
| 12 | 977.319 | 17.319 |
| 13 | 1052.645 | 12.645 |
| 14 | 1126.883 | 6.883 |
| 15 | 1200.000 | 0.000 |
| 16 | 1271.967 | −8.033 |
| 17 | 1342.754 | −17.246 |
| 18 | 1412.333 | −27.667 |
| 19 | 1480.675 | −39.325 |
| 20 | 1547.754 | −52.246 |
| 21 | 1613.546 | −66.454 |
Max error limited to 10 cents (only the first 11 frets may be used):
| Fret number | Cents | Deviation from 15edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 83.670 | 3.670 |
| 2 | 166.535 | 6.535 |
| 3 | 248.564 | 8.564 |
| 4 | 329.727 | 9.727 |
| 5 | 409.990 | 9.990 |
| 6 | 489.322 | 9.322 |
| 7 | 567.691 | 7.691 |
| 8 | 645.065 | 5.065 |
| 9 | 721.412 | 1.412 |
| 10 | 796.700 | −3.300 |
| 11 | 870.897 | −9.103 |
| 12 | 943.974 | −16.026 |
| 13 | 1015.899 | −24.101 |
| 14 | 1086.643 | −33.357 |
| 15 | 1156.178 | −43.822 |
| 16 | 1224.475 | −55.525 |
| 17 | 1291.509 | −68.491 |
16edo
Pure 2/1:
| Fret number | Cents | Deviation from 16edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 82.483 | 7.483 |
| 2 | 164.117 | 14.117 |
| 3 | 244.868 | 19.868 |
| 4 | 324.706 | 24.706 |
| 5 | 403.598 | 28.598 |
| 6 | 481.511 | 31.511 |
| 7 | 558.415 | 33.415 |
| 8 | 634.278 | 34.278 |
| 9 | 709.066 | 34.066 |
| 10 | 782.751 | 32.751 |
| 11 | 855.300 | 30.300 |
| 12 | 926.683 | 26.683 |
| 13 | 996.873 | 21.873 |
| 14 | 1065.840 | 15.840 |
| 15 | 1133.558 | 8.558 |
| 16 | 1200.000 | 0.000 |
| 17 | 1265.142 | −9.858 |
| 18 | 1328.962 | −21.038 |
| 19 | 1391.438 | −33.562 |
| 20 | 1452.550 | −47.450 |
| 21 | 1512.281 | −62.719 |
Max error limited to 10 cents (only the first 10 frets may be used):
| Fret number | Cents | Deviation from 16edo |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 78.993 | 3.993 |
| 2 | 157.011 | 7.011 |
| 3 | 234.022 | 9.022 |
| 4 | 309.995 | 9.995 |
| 5 | 384.898 | 9.898 |
| 6 | 458.700 | 8.700 |
| 7 | 531.369 | 6.369 |
| 8 | 602.877 | 2.877 |
| 9 | 673.193 | −1.807 |
| 10 | 742.290 | −7.710 |
| 11 | 810.140 | −14.860 |
| 12 | 876.717 | −23.283 |
| 13 | 941.997 | −33.003 |
| 14 | 1005.957 | −44.043 |
| 15 | 1068.574 | −56.426 |
| 16 | 1129.830 | −70.170 |
Bohlen–Pierce
As an example of a non-octave temperament, let's try to approximate the equal-tempered Bohlen–Pierce scale (13edt) by moving the bridge of a 12edo guitar.
The naive method of making the 13th fret an exact 3/1 would be terrible:
| Fret number | Cents | Deviation from 13ed3 |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 127.235 | −19.072 |
| 2 | 256.565 | −36.050 |
| 3 | 388.191 | −50.732 |
| 4 | 522.340 | −62.891 |
| 5 | 659.270 | −72.269 |
| 6 | 799.275 | −78.572 |
| 7 | 942.691 | −81.462 |
| 8 | 1089.910 | −80.552 |
| 9 | 1241.382 | −75.387 |
| 10 | 1397.638 | −65.439 |
| 11 | 1559.303 | −50.081 |
| 12 | 1727.124 | −28.568 |
| 13 | 1902.000 | 0.000 |
| 14 | 2085.028 | 36.720 |
| 15 | 2277.566 | 82.951 |
| 16 | 2481.323 | 140.400 |
Even though the error of the 13th fret is 0, the error of frets 7 and 8 is about 80 cents, which is unacceptable.
A much more satisfactory solution is to minimize the maximum error over the first 6 frets:
| Fret number | Cents | Deviation from 13ed3 |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 138.788 | −7.520 |
| 2 | 280.853 | −11.763 |
| 3 | 426.563 | −12.360 |
| 4 | 576.345 | −8.886 |
| 5 | 730.697 | −0.841 |
| 6 | 890.206 | 12.360 |
| 7 | 1055.569 | 31.415 |
| 8 | 1227.620 | 57.158 |
| 9 | 1407.376 | 90.606 |
Or even just the first 5, for better accuracy:
| Fret number | Cents | Deviation from 13e3 |
|---|---|---|
| 0 (nut) | 0.000 | 0.000 |
| 1 | 140.285 | −6.023 |
| 2 | 284.014 | −8.601 |
| 3 | 431.581 | −7.343 |
| 4 | 583.443 | −1.787 |
| 5 | 740.140 | 8.601 |
| 6 | 902.305 | 24.459 |
| 7 | 1070.696 | 46.543 |
| 8 | 1246.229 | 75.768 |
If the open strings are tuned in 9/7s or 7/5s, this makes a perfectly playable BP guitar with fret error under 9 cents. The only restriction is that you should never play frets 6 or above, because they're increasingly out of tune.
Advanced tricks
By adjusting the nut in addition to the bridge, it may be possible to make a surprisingly large portion of the fretboard usable with good accuracy. This is because there is another degree of freedom to tweak. For decreasing the EDO number you would want to either raise the nut or move it away from the first fret, and for increasing the EDO number you would want to either lower it or move it towards the first fret.