Dave Keenan & Douglas Blumeyer's guide to RTT: tuning in nonstandard domains

This is article 9 of 9 in Dave Keenan & Douglas Blumeyer's guide to RTT, or "D&D's guide" for short. This concluding chapter assumes much of the knowledge that comes from the earlier chapters, so we encourage readers to get up to speed with that material before digging into the stuff covered here.

At the time of this writing, not much has been done regarding the novel problems involved with optimizing tunings for regular temperaments of nonstandard domains.

If "nonstandard" is taken to mean "non-prime-limit" (as we think it's a good idea to do), then there's nothing fundamentally different about tuning a temperament of 2.3.7 than there is to tuning a temperament of 2.3.5. These prime-subgroup domains do not raise novel tuning problems, at least not conceptual ones (i.e, you may have to refactor your tuning code to accommodate the fact that the third entry may not always correspond to prime 5, but that's the extent of the problem).

At the other extreme, "nonstandard" may be taken to mean "irrational". That is, we might find a temperament whose basis includes the golden ratio, ɸ, in order to achieve a sort of anti-JI effect. But we won't be considering these sorts of temperaments here, and that is because irrational numbers cannot be factored into primes.

The bulk of this article section will deal with nonstandard bases between these two extremes. Things get interesting when we think about possibilities for tuning temperaments with nonprime domain bases, i.e. those which are still rational (JI) but include nonprime basis elements such as 9, or 5/3. As far as we know, this topic has only been written about in the context of a single pair of all-interval tuning schemes: minimax-S and minimax-ES (see: Tp tuning). On the Tp tuning wiki page, two possible approaches are presented for tuning temperaments with nonprime bases. It calls these approaches the "subgroup notion" and the "inharmonic notion". We prefer the terminology prime-based and nonprime-based, respectively, for reasons that we will explain soon. But in fact, the choice between these two approaches is relevant to any conceivable tuning scheme applied to a temperament with a nonprime basis. This is to say that there's nothing specific to these two all-interval schemes about the choice between "prime-based" and "nonprime-based".

But not only has this choice only been written about with regards to a mere two tuning schemes, it appears only to have been applied to a single one of those, in a single context. This context is Graham Breed's online tuning app x31eq, and that single tuning scheme is Graham's favored tuning scheme: minimax-ES. He did invent it after all. He calls it "Tenney-Euclidean", or "TE", and so in his app these two variations for temperaments with nonprime bases are called "subgroup TE" and "inharmonic TE" (so for us, those'd be "prime-based minimax-ES" and "nonprime-based minimax-ES", respectively).

The goal with this section of this article is to explain what this fundamental choice regarding nonprime-basis temperament-tunings is all about, and speak to why one might prefer using one approach to the other. We will also introduce the fact that one may choose to take neither of these two approaches, a possibility which does not seem to have been addressed in the practice thus far. We will discuss the topic in a way that effectively generalizes it to all nonprime-basis tuning schemes, as it should be. Finally, we will also work through the computation process for both approaches.

The three approaches

One property of prime numbers (that has particular relevance for the way we do things in RTT) is being building blocks for the rational numbers; this property taps into the way we take the prime factorizations of rational numbers and put them into vector form and do linear algebra on them with transformation matrices and such. When composers or theorists use a domain basis that includes nonprimes, such as the basis 2.9.7/5, they are designating these numbers as their "basis elements" instead, thereby asking us to treat them as protected-against-prime-factoring. So when notating, or building scales and chord progressions on lattice diagrams, or whatever, these basis elements are what shape what's possible to do musically, and how.

One of our considerations is: having chosen a nonprime basis like this, how to approach optimizing its tuning? Here are three possible options:

• With the prime-based approach, we temporarily factor all of the basis elements of our nonprime basis into primes. This essentially means that we've embedded our temperament into a new domain, a larger one, i.e. a superspace of the original domain, and not just any superspace, but specifically the one with the simplest prime-only basis (or SPOB for short). Once we've achieved this, we can tune with respect to any target-intervals we want in that superspace, then convert back to the original nonprime basis as a final step. (For all-interval tunings such as minimax-ES, the assumption is that we take advantage of this by choosing the primes of the prime-only basis of this superspace as our target-intervals.)
• With the nonprime-based approach, we choose to not break our basis down into its prime elements. And when computing any interval complexities whose reciprocals are used as damage weights, we also refuse to prime factor their basis elements.
• With the neutral approach, we simply tune as we normally would, which is to say that we don't do any manipulation of the basis (prime factoring or otherwise), but when computing interval complexities we will prime factor intervals as per usual.

Given this explanation, our nomenclature for these approaches should be clear now (there are explanations for the names "subgroup" and "inharmonic", of course, but we don't think they're nearly as clear as ours). When you're working with a temperament of a domain with any nonprime basis elements, then the "prime-based" approach factors them into actual primes and tunes with respect to those (then unfactors), whereas the "nonprime-based" approach preserves your nonprime-based intervals as they are, unbroken. While the neutral approach leads to neither of those special things happening.

And so now we can see why this choice wouldn't have made any difference for temperaments of the domain 2.3.7. What standard superspace would you embed that in? What basis element needs prime-factorization here? Its basis elements are already as prime-factored as they can go, in either case.

Note on coprime

We note that while the Tp tuning page claims that the choice between approaches only matters when two basis elements share a prime factor, or in other words, that the choice doesn't matter for coprime bases such as 2.9.5 or 2.5/3.7, this is true of "Tₚ tunings" such as minimax-ES as used on Graham's app and minimax-S, however, this is not true in general when the prime-based and nonprime-based approaches are extended to apply to ordinary non-all-interval tuning schemes, alternative complexities, etc.

In particular, when following a scheme whose target-interval set is itself determined by a scheme (such as TILT), it is likely to result in a different set of target-intervals depending on whether you're tuning in the original nonprime basis or the standard superspace which will support many more different target-intervals.

How to choose your approach

Now we suppose you must be wondering: why would anyone have a preference among these three approaches to tuning optimisation? What would the actual effect on the tuning be? Those are both excellent questions, and we will cover both of those before this section is up.

There are valid reasons to prefer the prime-based or the nonprime-based approach, but we feel the clear default here is choosing neither one.

We'll begin with a sort of flowchart to help you choose your favored approach (of course, your preference may change from one piece of music to the next, but that's another issue):

• Do you wish to use the opportunity of having chosen a nonprime domain basis to explore experimental new possibilities of tuning optimization, essentially exploring alternate realities where your basis elements really were protected-against-prime-factoring? Choose the nonprime-based approach.
• Are you not interested in (or actively against the idea of) such experimentation, not really thinking of your choice of a nonprime domain basis as a tuning choice like that, but rather thinking of it as a compositional constraint in terms of how it affects your lattice and such? Choose the neutral approach, unless:
• You are also optimizing the tuning of this temperament for simultaneous (or near simultaneous) performance with other temperaments that share the same SPOB (simplest prime-only basis), and you wish for the tunings to match better across them. Choose the prime-based approach.

Prime-based

The distinguishing characteristic of the prime-based approach is that it's the only one which supports tuning with respect to intervals that you can't actually reach to play in the temperament. For example, you would choose the prime-based approach to tuning a temperament of the 2.5/3.7 domain if you still want prime 5 and prime 3 to be individually optimized for, even while you are preventing yourself from ever using them in isolation from each other.

Now, putting it that way, this approach seems not logical, though. But that's because we haven't included all of the reasoning yet. So you would only choose to do that if you also intended to integrate this music you're writing — with no lone 5's or lone 3's, only the 5/3 — with other music (whether actually simultaneously or in quick succession) that is written in temperaments with other nonprime bases that share the same SPOB (which would be collectively tuned with respect to this shared superspace basis) and/or temperaments of this SPOB itself, which would contain the lone 5's or 3's. In other words, the prime-based approach only makes sense if you are using the subspacing to compositionally constrain yourself in one place or another at one time — one voice, one movement, etc. — but ultimately recognize that the music is still fundamentally built out of the actual primes, and you make use of those primes somewhere at some point.

Said another way, you still view the music as "truly being in" the SPOB (the one found by the prime factorization of your basis elements), but have chosen to use a subspace of it in order to restrain yourself from accessing certain intervals or chords.

Note that if you don't actually use any of the new intervals afforded to you by the change of basis to the superspace, you will not find a different tuning than you would by the neutral approach here. That's because it's only the nonprime-based approach which actually changes how complexity is measured.

The prime-based approach is the preferred approach of the tuning theorist and composer Flora Canou for these reasons.

Nonprime-based

With the nonprime-based approach, you are essentially trying to make music as if in a world where certain primes never existed at all.

Now, this statement is always trivially true, since no one uses all the primes up to infinity; most people cut off before getting much further than prime 13. But what we mean here is more the effect of, say, to use the same example from the previous section, to paint a musical picture in a world where it's as if prime 3 and prime 5 never existed, and all that ever existed was this 5/3 interval.

The key defining characteristic of this approach is that when computing interval complexity, one is forbidden from thinking of the nonprime basis elements as prime factorizable. For example, in the computation of log-product complexity, if 9/7 was one of our nonprime basis elements, then its log-product complexity would be [math]\log_2{\frac97}[/math] rather than the usual [math]\log_2{9·7}[/math].

So the nonprime-based approach is for those people who wish to actually go a bit further into the promise of the experimental territory of nonprime bases.

The nonprime-based approach is the default approach used by Graham Breed's temperament app.

We note that on account of this difference in pre-scaling within the double bars of the [math]1[/math]-norm, there is an argument that nonprime-based minimax-ES is not actually using the default complexity of [math]\text{lp-C}()[/math], or that what we've been considering to be log-product complexity this whole time should more accurately have been thought of exclusively in its vector-based form, never its quotient-based form, i.e. the way more directly akin to copfr and sopfr that might more fittingly be referred to as "lopfr" for logs-of-prime-factors-with-repetition! But there's also an argument that [math]\log_2{\frac97}[/math] can still be seen as the log-product complexity of 9/7 when you realize that if 9/7 is considered a basis element, that means that it's not actually allowed to be broken down into a numerator and denominator; if anything, it would be [math]\frac{9/7}{1}[/math], i.e. the numerator is 9/7 and the denominator is 1. In other words, its the nonprime-based approach which should be the thing that shoulders the burden of this sort of weirdness, not any complexity functions; the nonprime-based approach redefines reality broadly and you just have to think about these sorts of things on a case-by-case basis, how things work differently if 9/7 is now protected-against-prime-factoring.

Neither

The neutral approach is the most straightforward to understand the motivation for. This is about optimizing the tuning for the specific temperament at hand, with no considerations either made for inter-temperamental music-making such as we've seen is the motivation for the prime-based approach, nor for the experimental treatment of the nonprimes as intervals protected-against-prime-factoring for tuning purposes as we see with the nonprime approach.

This approach is for people who think of the use of a nonstandard domain basis primarily as a compositional constraint, like the prime-based folk do, however, unlike the prime-based folk, these people have no interest in tuning with respect to the SPOB in order for synergy with other temperaments to be played together with the one at hand.

Considering that the RTT community's command of ordinary tuning schemes — i.e non-all-interval ones, which ask the user to specify their target interval set — has been so stunted historically, we consider it an important warning here that if optimizing your tuning for nonprime intervals is your only consideration, there are much better ways to do it than choosing a nonprime domain basis and tuning it with this neutral approach. In that case, you are probably experiencing what might be deemed "target-interval-set envy", and should instead consider exploring how inclusion and exclusion of particular intervals from your target-interval set affects your tuning.

Illustrative example

Let's consider an example. We won't be working through the computation method here yet; at this point we seek only to illustrate the points made in the previous example by showing how the tuning map is affected for a specific real-world case depending on the choice of prime-based or nonprime-based tuning. This example will use minimax-ES, whose use with these two approaches has already been well-established. (In the computation section coming up next, though, we will do more to work toward generalizing this concept beyond it, though, by demoing its use with a completely different tuning scheme.) Remember, minimax-ES is an all-interval tuning scheme, so our target-intervals are only proxy targets for all the intervals, and also, these proxy targets are always our basis elements (in the standard cases we've looked up until this point, they've always been our primes).

The temperament we'll be looking at for this example is called marveltri, and it's a temperament of the 2.5.9/7 domain, with mapping [math]M[/math] = [⟨1 2 1] ⟨0 1 -2]}. See http://x31eq.com/cgi-bin/rt.cgi?limit=2_5_9%2F7&ets=22_69 for details of this example. Intuitively, we should expect the nonprime-based tuning to tune the nonprimes better than the prime-based tuning would. In this case we have just the one nonprime: 9/7. Hopefully that prediction is self-explanatory.

Nonprime-based

Following the nonprime-based approach, we find our retuning map [math]𝒓 =[/math] ⟨0.826 -1.781 -0.022]. And so we're off to a good start: with only about one-fiftieth of a cent of absolute error, our nonprime 9/7 is essentially unchanged! (and tuned better than either of the other two actual primes).

Prime-based

Under the prime tuning, then, we find a retuning map [math]𝒓 =[/math] ⟨0.598 -1.289 -2.144]. Indeed, the error on the nonprime 9/7 is nearly 100 times worse now, and is the worst of any of our three basis elements. However, we may note that the tunings of both the actual primes improved slightly.

So let's dig into why exactly the prime-based approach led to this result.

We know that the prime-based approach works by embedding into the simplest prime-only superspace. With our nonprime basis 2.5.9/7, our SPOB (simplest prime-only basis) is going to:

1. disentangle the 7 from the 9, and
2. access all powers of 3, not just the even ones via 9

So that takes us to the superspace 2.3.5.7. Here is this domain basis:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{5} \\ \scriptsize{7} \\ \end{array} \end{array} \begin{array} {ccc} B_{2.3.9/7} \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{5} & \scriptsize{9/7} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{array} \right] \end{array} [/math]

This matrix can perhaps most easily be read in terms of its columns; we can see it as expressing the basis elements of our nonprime domain basis in terms of the actual underlying primes: 2 as [1 0 0 0⟩, 5 as [0 0 1 0⟩, and 9/7 as [0 2 0 -1⟩. We can use this matrix to convert our temperament from its current nonprime basis to this SPOB. We can't convert our mapping directly from the subspace to the superspace, but what we can do is convert the corresponding comma basis [math]\mathrm{C}[/math] which is a basis for the nullspace of our mapping and which also defines our temperament. That's ⟨[-5 2 1⟩], or in other words [math](\frac21)^{-5} × (\frac51)^2 × (\frac97)^1 = \frac{25×9}{32×7} = \frac{225}{224}[/math], so it's a matrix containing a single column vector for the marvel comma but expressed with the 2.5.9/7 domain basis.

We can say already, then, that this example temperament we chose — "marveltri" — is in fact marvel temperament, or we could say more precisely that it is a reformulation of it with an additional constraint. While in a standard domain we think of the marvel comma as [math]\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·3·3·5·5·\frac{1}{7}[/math], here we group up the 3's and the 7 and define that interval to be protected-against-prime-factoring, i.e. designate it as a basis element, and so instead the comma we're tempering out becomes interpreted as [math]\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·\frac{1}{2}·5·5·\frac{9}{7}[/math].

We can confirm this fact with our domain basis matrix, which doubles as a basis-changer. Simply convert our comma basis in the nonprime basis [math]\mathrm{C}_{2.5.9/7}[/math] to the standard domain equivalent [math]\mathrm{C}[/math]. Note that when moving from the subspace to the superspace, we left-multiply by the basis-changer (see here for more information). We've reversed the usual direction of data flow here by putting the calculation on the right and its result on the left, and we've indicated this with an arrow under the equals sign, because we think it will be easier to keep track of what's happening if we always put the superspace on the left and the subspace on the right.

[math] \begin{array} {ccc} \\ \begin{array} {rrr} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{5} \\ \scriptsize{7} \\ \end{array} \end{array} \begin{array} {ccc} \mathrm{C} \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} -5 \\ 2 \\ 2 \\ -1 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\huge ⭀} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{5} \\ \scriptsize{7} \\ \end{array} \end{array} \begin{array} {ccc} B_{2.5.9/7} \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{5} & \scriptsize{9/7} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\large ×} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{5} \\ \scriptsize{9/7} \\ \end{array} \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} \begin{array} {ccc} \mathrm{C}_{2.5.9/7} \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} -5 \\ 2 \\ 1 \\ \end{array} \right] \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} [/math]

Indeed, here is the more familiar standard vector for the marvel comma, [-5 2 2 -1⟩. And to further confirm, when we do a column-wise nullspace on this comma, we get [⟨1 0 0 -5] ⟨0 1 0 2] ⟨0 0 1 2]}, which is the mapping for 7-limit marvel temperament.

So, again, this is telling us that one way to think of this temperament [⟨1 2 1] ⟨0 1 -2]} is that it's 7-limit marvel (the marvel comma is made to vanish) except where we don't have access to just any old interval with factors of prime 3 or 7; any factor of prime 7 is necessarily accompanied by two factors of prime 3 (and you can still manage to make the marvel comma vanish that way, because that comma contains that [math]\frac97[/math] interval). The point is: we can think of the tuning we found with the prime-based approach as if we had simply tuned marvel, then thrown away our ability to actually use a lot of those intervals we tuned for.

We should, then, be able to confirm that this is the same tuning we would have chosen had we simply decided to compose with marvel in its standard domain, and use this to learn why [math]\frac97[/math] ended up with -2.144 ¢ error here, so much more than it did with the nonprime-based approach. When we check the minimax-ES tuning of marvel (see: http://x31eq.com/cgi-bin/rt.cgi?ets=72_31_53&limit=7), which gives [math]𝒓 =[/math] ⟨0.598 -0.601 -1.289 0.942], we can see that the absolute error for each prime rounds to 1 ¢; it's a pretty middle-of-the-road tuning, just the sort of thing you'd expect and want from a (pretransformed) [math]2[/math]-norm, minimizing neither the max nor the total of the damages but somewhere in between, but the key thing to note is what that entails for the interval [math]\frac97[/math], which from marvel's perspective is just one of many many intervals you can make out of 2's, 3's, 5's, and 7's. Notice that while the absolute errors for all the primes are about the same, critically, the signs on the errors for prime 3 and 7 are opposite: prime 3 is tuned narrow while prime 7 is tuned wide. So when they appear on opposite sides of the quotient bar, as they do in [math]\frac97[/math], the errors are going to compound, and the interval will be tuned doubly-narrow. And indeed we find that summing the errors of the constituent primes -0.601 + -0.601 - 0.942 = -2.144, exactly what we were expecting.

The prime-based tuning of marveltri is {1200.5978 383.8288] and can be found here: http://x31eq.com/cgi-bin/rt.cgi?limit=2_5_9%2F7&ets=22_69&subgroup=on

The story for the nonprime-based approach, on the other hand, is much simpler: we tuned [math]\frac97[/math] as best we could, given the constraints that the other basis elements, [math]2[/math] and [math]5[/math], also needed to be tuned well. And we ended up with a really, really accurate tuning of [math]\frac97[/math] doing it that way.

Neutral

Going the neutral route, we find a tuning map [math]𝒕 = [/math] ⟨1200.598 2785.025 432.940], which means a retuning map of [math]𝒓 = [/math] ⟨0.598 -1.289 -2.144]. So in this case it's identical to the prime-based result. Which makes sense, because we're measuring complexity in the same way here, and our basis elements are coprime. But again, this won't always be the case, as we'll see with our example in the computation section below.

Regarding target-interval sets

Now that we've gotten that example out of the way, which used the established, but all-interval, minimax-ES to illustrate the essence of the choice between these three approaches, we're ready to start focusing on ordinary tuning schemes, i.e. non-all-interval tuning schemes, and the problems involved in their target-interval set specification.

Quotient-based vs vector-based specification

When manually specifying the target-interval set for a prime-based tuning scheme, and providing the target intervals in vector form, they should all be given in the SPOB (the simplest prime-only basis), because that's the only basis where all of them could be described. When doing this for the other two approaches, though, of course as usual you should give them in the same basis that the temperament mapping is given in. This issue does not arise if you specify your target-intervals in quotient form.

For example, we might have the "prime-based {2/1, 4/3, 10/7, 3/2, 15/7, 7/5} miniaverage-U" tuning of some temperament in the 2.3.7/5 basis. If we wanted to give those target-intervals in vector form, then for the neutral and nonprime-based approaches, we would give those as { [1 0 0⟩, [2 -1 0⟩, [1 0 -1⟩, [-1 1 0⟩, [0 1 -1⟩, [0 0 1⟩ }. However, for the prime-based approach, it would only make sense to give those as { [1 0 0 0⟩, [2 -1 0 0⟩, [1 0 1 -1⟩, [-1 1 0 0⟩, [0 1 1 -1⟩, [0 0 -1 1⟩ }.

But even that doesn't quite make sense, because why are we using the prime-based approach here (as opposed to the neutral approach) if we're not taking advantage of the independence of primes 5 and 7? We should only do this if we're also going to include target-intervals such as 5/4, 6/5, and 7/4.

Scheme filtering

Regarding target-interval set schemes, such as the truncated integer limit triangle, or TILT, the most logical-seeming way to handle them is to compute them as normal, then filter out any intervals unsupported by the basis. For example, take the 8-TILT. Normally that would be {2/1, 3/1, 3/2, 4/3, 5/2, 5/3, 5/4, 6/5, 7/3, 7/4, 7/5, 7/6, 8/3, 8/5}. However, if we've asked for the TILT miniRMS-S tuning of some temperament in the 2.3.7 basis, we can't use several of those intervals; instead, TILT here should be understood to give {2/1, 3/1, 3/2, 4/3, 7/3, 7/4, 7/6, 8/3} only. This issue is pertinent not only to nonprime bases, but indeed any basis which even so much as skips a prime.

And so, when we compare "TILT minimax-ES" or "TILT nonprime-based minimax-C" with "TILT prime-based minimax-ES", there's actually more difference between the schemes than whether or not we change basis to the SPOB, or revise our complexity formulas to prevent the factorization of our nonprime basis elements; there's also the difference in results from the target-interval set scheme within the tuning scheme. This is implicit in all-interval tunings where the target-interval set scheme is not explicitly specified and is thus assumed to be the primes — at least the proxy targets are the primes, and by primes we actually mean more generally the basis elements. In other words, we could say that for the "minimax-ES" tuning scheme, our target-interval set scheme is actually the "all-intervals-as-proxied-by-the-basis-elements" scheme, which like any target-interval set scheme as described above, is understood to translate into a different set of target-intervals depending on the basis.

Default max

We also need to address how the default max integer for the TILT should be computed (and the default max odd for the OLD, etc.). Previously, when working only with standard (prime-limit) bases, we defined it to be the integer one less than the next prime above the prime limit. But that definition may not be the best in general.

Consider the basis 2.9.21. The current definition would give us the 10-TILT, since 7 is the prime limit of this basis, 11 is the next prime after that, and 10 is the integer one less than that. But it seems pretty clear that if someone is interested in 21/1 as a basis element, then they'll certainly be interested in tuning some target-intervals which include 21's in them, but the 10-TILT won't have any of those, considering its integer limit is less than half of that!

So, we suggest that the better generalization of the definition of the max integer for TILT is actually one less than the next prime above the integer limit of the basis. Whenever the basis is prime-only (standard or otherwise, i.e. this works for 2.3.5.7 but also 2.3.7), this will come out to the same thing.

Regarding our example, then, the integer limit of that basis is 21, the next prime is 23, and so the default TILT here is the 22-TILT (filtered, of course, of all intervals with 5's, 11's, 13's, 17's, and 19's in their factorizations, or odd counts of 3's).

Computation

For this example, we'll tune a temperament of the 2.7/3.11/3 domain with the TILT minimax-C tuning scheme.

Neutral

First, let's go through the neutral approach, which is the simplest, on account of it essentially being the do-nothing-different approach.

Here's our mapping, which gives us a ~[math]\frac21[/math] period and ~[math]\frac{12}{11}[/math] generator:

[math] \begin{array} {ccc} \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr}\\ \\ \\ \\ \end{array} \\ \end{array} \begin{array} {c} M_s \\ \begin{array} {lll}  & \scriptsize{2} & \scriptsize{\frac{7}{3}} & \scriptsize{\frac{11}{3}} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 1 & 2 \\ 0 & 2 & -1 \\ \end{array} \right] \\ \end{array} [/math]

And here's what our just tuning map looks like in this nonprime basis, just the cents per basis element for each of 2, 7/3, and 11/3:

[math] \begin{array} {ccc} \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} \begin{array} {c} 𝒋_s \\ \begin{array} {lll}  & \scriptsize{2} & \quad\quad\quad \scriptsize{\frac73} \quad\quad\quad & \scriptsize{\frac{11}{3}} \\ \end{array} \\ \left[ \begin{array} {rrr} 1200 & 1466.871 & 2249.363 \\ \end{array} \right] \\ \end{array} [/math]

As for our target-interval set, the TILT, or truncated integer limit triangle, defaults to the highest integer limit within the prime limit, so in our case, even though we're not using a prime limit as our domain basis, our maximum prime is 11, so that makes 12 our max integer for purposes of the TILT. But we can't accept every interval in the 12-TILT, because it contains a bunch of them with factors of 5, or factors of 3 unaccompanied by factors of 7 or 11, etc. So we end up with a subset of the 12-TILT, namely [math]{ \frac21, \frac73, \frac76, \frac{11}{6}, \frac{11}{7}, \frac{12}{7} }[/math]. So that gives us a target-interval list in matrix form:

[math] \begin{array} {ccc} \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{\frac73} \\ \scriptsize{\frac{11}{3}} \end{array} \end{array} \begin{array} {c} \mathrm{T}_s \\ \left[ \begin{array} {r|r|r|r|r|r} 1 & 0 & -1 & -1 & 0 & 2 \\ 0 & 1 & 1 & 0 & -1 & -1 \\ 0 & 0 & 0 & 1 & 1 & 0 \\ \end{array} \right] \\ \end{array} [/math]

And here's our complexity weight matrix, using our default log-product complexity:

[math] \begin{array} {c} C_s \\ \left[ \begin{array} {c} \log_2{2·1} & 0 & 0 & 0 & 0 & 0 \\ 0 & \log_2{7·3} & 0 & 0 & 0 & 0 \\ 0 & 0 & \log_2{7·6} & 0 & 0 & 0 \\ 0 & 0 & 0 & \log_2{11·6} & 0 & 0 \\ 0 & 0 & 0 & 0 & \log_2{11·7} & 0 \\ 0 & 0 & 0 & 0 & 0 & \log_2{12·7} \\ \end{array} \right] \end{array} [/math]

This matrix is shown with [math]\text{lp-C}()[/math] computed using its quotient-based form, i.e [math]\log_2{\!n·d}[/math], which requires no modification to perform correctly in this nonprime basis situation. However, we note that if one prefers the vector-based form, i.e. the pretransformed norm, one should be careful with the diagonal entries of the pretransformer. For an all-integer domain basis such as  2.9.7.11 this issue wouldn't make a difference, but it does make a difference if your basis contains rationals such as ours does. The issue is that one cannot simply set each basis element's pretransformer entry to its log, one must set it to its own log-product complexity. For example, for our second basis element, its pretransformer entry should be [math]\log_2{7·3}[/math], not [math]\log_2{\frac73}[/math]. Here's our full complexity pretransformer, for clarity:

[math] \begin{array} {ccc} \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{\frac73} \\ \scriptsize{\frac{11}{3}} \\ \end{array} \\ \end{array} \begin{array} {c} \begin{array} {lll} X \\ \end{array} \\ \left[ \begin{array} {c} \log_2{2·1} & 0 & 0 \\ 0 & \log_2{7·3} & 0 \\ 0 & 0 & \log_2{11·3} \\ \end{array} \right] \\ \end{array} [/math]

Okay, where to from here? Well, it's rather straightforward at this point. We just plug these objects into whatever pertinent optimization method. The result should be: [math]𝒈[/math] = ⟨1194.291 135.186].

Nonprime-based

Everything's the same from the neutral approach to the nonprime approach, except that we may need to modify some complexity calculations. In our case, we're changing our pre-transformer matrix slightly:

[math] \begin{array} {c} C_s \\ \left[ \begin{array} {c} \log_2{2·1} & 0 & 0 & 0 & 0 & 0 \\ 0 & \log_2{\frac73} & 0 & 0 & 0 & 0 \\ 0 & 0 & \log_2{\frac73·2} & 0 & 0 & 0 \\ 0 & 0 & 0 & \log_2{\frac{11}{3}·2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \log_2{\frac{11}{3}·\frac73} & 0 \\ 0 & 0 & 0 & 0 & 0 & \log_2{2^2·\frac73} \\ \end{array} \right] \end{array} [/math]

Which gives a different result, [math]𝒈[/math] = ⟨1198.336 136.833].

Prime-based

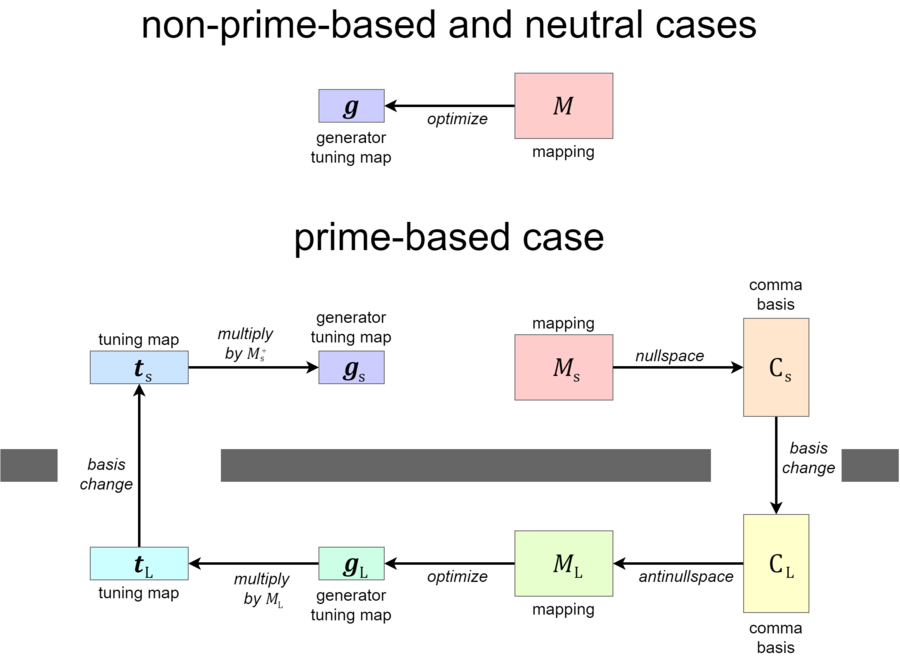
Finally, we'll look at the prime-based approach. We already briefly touched at how some of this looks in the example section above, in the course of explaining how the tuning of marveltri changes depending on your approach, prime-based or nonprime-based. But we're going to go through all the steps this time around. This process was inspired by the one described here: Generalized_Tenney_Norms_and_Tp_Interval_Space#Examples.

At the high level, this is what we're going to do:

1. Find a comma basis of our temperament, as a basis for the nullspace of our mapping.
2. Prepare a matrix which we'll use to convert our temperament from its nonprime basis over to the simplest possible standard (prime-only) domain basis.
3. Go ahead and change our temperament's basis in this way, doing so by multiplying the comma basis we found in step 1 with the basis change matrix we prepared in step 2, in order to compute what our comma basis looks like in the prime-only domain basis.
4. Using the nullspace operation, find a mapping for this new temperament, which is the same as the old temperament except that it has this prime-only domain basis.
5. Determine target-intervals and held-intervals as desired and afforded by this superspace. And determine the weights for the target-intervals.
6. Optimize for a generator tuning map as usual, using the mapping from step 4 and the tuning targets from step 5.
7. Convert the generator tuning map to the tempered-prime tuning map, so we can change its domain basis.
8. Change domain basis from the temporary standard domain basis back into the original nonprime basis.
9. Find the pseudoinverse of the mapping, in order to convert this tempered-prime tuning map into a generator tuning map with a form which matches the mapping.
10. Convert to a generator tuning map using this pseudoinverse from the previous step.

And then we're done! We wish we could say it was possible in 3 easy steps, but it's more like 10 medium-hard steps.

It looks like this:

For the duration of this section, we will be subscripting objects in the original 2.7/3.11/3 basis with [math]s[/math], for "smaller" space, and objects in the SPOB 2.3.7.11 with [math]L[/math], for "larger" space (AKA superspace).

1. Find comma basis

We expect the reader to understand why we temporarily change basis to a basis for another domain in order to tune our temperament, and then change back; this is, after all, the entire point of this tuning approach. But we also expect there are many readers who are uncertain as to why it is the case that as part of this process it is apparently necessary to convert our mapping temporarily into a comma basis in order to change domain basis, and then convert back. Why should this be necessary — why can't we cut off the two "comma basis" nodes of the diagram above, going straight from the original mapping to the standard domain mapping?

The short answer is: because one can only directly change the basis of a mapping to a subspace of its current space, not a superspace. And vice versa, one can only directly change the basis of a comma basis (the dual manner of representing temperaments) to a superspace, not a subspace. And since it's a superspace that is our destination, we must get there via a comma basis detour. The full explanation for this necessity is beyond the scope of this computation example, however, we encourage the reader to review the material here (Temperament_merging_across_interval_bases#Application:_determining_whether_it_is_possible_to_change_the_interval_subspace) if interested.

So, how to find the comma basis from the mapping? Easy enough. By using the nullspace operation on the mapping. The method of finding this is explained here: Dave Keenan & Douglas Blumeyer's guide to RTT: exploring temperaments#Nullspace. Here's what you should find:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{\frac{7}{3}} \\ \scriptsize{\frac{11}{3}} \\ \end{array} \end{array} \begin{array} {ccc} \mathrm{C}_s \\ \begin{array} {ccc} \end{array} \\ \left[ \begin{array} {rrr} 5 \\ -1 \\ -2 \\ \end{array} \right] \end{array} [/math]

So that's [math]2^{5}(\frac73)^{-1}(\frac{11}{3})^{-2}[/math], or in other words, [math]\frac{32×27}{7×121} = \frac{864}{847}[/math], a comma about 34.4 ¢ in size.

2. Prepare basis change

With our nonprime basis of 2.7/3.11/3, our SPOB is going to need to disentangle both the prime 7 and the prime 11 from their respective prime 3's. This will lead us to the superspace 2.3.7.11, or in other words, the 11-limit except without any prime 5.

Another way to think about this SPOB is just the set of actual primes we would need to be able to express all of our nonprime basis elements as vectors. Because that's essentially what we're going to do! When we represent our domain basis in this fashion, we actually get another powerful result for free. The resultant matrix can be used to transform intervals from the nonprime basis we're describing into that SPOB — intervals such as commas, and in particular our temperament's comma basis.

Here is this domain basis:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{7} \\ \scriptsize{11} \\ \end{array} \end{array} \begin{array} {ccc} B_s \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{\frac73} & \scriptsize{\frac{11}{3}} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & -1 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} [/math]

Note that even though we're in a sense going from our weird nonprime basis and "getting to basics" here, we still don't necessarily go all the way to the most basic thing, which would be a prime limit. That is, we don't include an all-zeros row for prime 5 even though our temperament doesn't deal with it, just for simpleness' sake we can say we're in a prime limit and so we find all the primes in their typically expected positions (so that we're not surprised when the 3rd prime here is 7 and the 4th is 11, instead of those being the 4th and 5th, respectively). It's not just a cosmetic thing either. Adding that extra row essentially means that the output intervals will have one more dimension than they did before. And remember the everpresent formula [math]d = n + r[/math], that is, dimensionality equals nullity plus rank. So any increase in dimensionality will correspond to a change in either nullity or rank. Which opens the impossible-to-answer question of: which comma do we add to this temperament on account of converting its basis, etc. Just unask the question, and don't add new rows for primes your temperament doesn't deal with.

3. Change domain basis

To effect the basis change, we simply matrix multiply our comma basis by the basis change. We put the transformation matrix on the left, just like we would for any interval vector, or list thereof, with a temperament mapping matrix.

[math] \begin{array} {ccc} \\ \begin{array} {rrr} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{7} \\ \scriptsize{11} \\ \end{array} \end{array} \begin{array} {ccc} \mathrm{C} \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} -5 \\ -3 \\ 1 \\ 2 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\huge ⭀} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{7} \\ \scriptsize{11} \\ \end{array} \end{array} \begin{array} {ccc} B_s \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{\frac73} & \scriptsize{\frac{11}{3}} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & -1 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\large ×} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{\frac{7}{3}} \\ \scriptsize{\frac{11}{3}} \\ \end{array} \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} \begin{array} {ccc} \mathrm{C}_s \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} 5 \\ -1 \\ -2 \\ \end{array} \right] \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} [/math]

We can double-check that this is the same comma: [math](2)^{-5}3^{-3}7^{1}11^{2} = \frac{7×121}{32×27}[/math]. Again, yes, this is [math]\frac{864}{847}[/math].

So this is our new comma basis. It's the same one comma, but as tempered by a temperament in the 2.3.7.11 space.

4. Find mapping

To get us back into the form of a mapping — which we'll need in order to optimize the temperament's tuning as we've been practicing throughout this article series — we again need to use the nullspace operation (though this time we do it column-wise).

With that, we find:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \\ \\ \\ \end{array} \end{array} \begin{array} {ccc} M_L \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{3} & \scriptsize{7} & \scriptsize{11} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 1 & 2 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 2 & -1 \\ \end{array} \right] \end{array} [/math]

So again, this is the same as the old temperament, except that it has this prime-only domain basis. (We're still labeling its rows or columns and using subscripts to indicate its domain basis, since it may be prime-only, but on account of the gap where it skips prime 5, it is still not standard.)

Note that by splitting our two basis elements 7/3 and 11/3 up into three basis elements 3, 7, and 11, we have increased dimensionality of our temperament by 1. And our temperament's identity is based on its comma basis, so our nullity hasn't changed. Therefore, by the rank-nullity theorem which states that dimensionality [math]d[/math] must equal rank [math]r[/math] plus nullity [math]n[/math], we can see that our temperament's rank must go up by 1 in this new basis. And indeed we can see that while our mapping used to have only 2 rows, it now has 3 rows, each corresponding to a generator. Unlike the consequences we warned against of spuriously adding a blank row for the unused prime 5, this change in [math]d[/math], [math]n[/math], and [math]r[/math] is very real. What this means is that when we run our optimization procedure, we will be imagining as if we have three generators in our temperament, even though we know that in our actual original basis it only has two. In the end, we'll convert our three-entry generator tuning map from this superspace basis back down into a two-entry generator tuning map, by consolidating those generators together. This is one way of looking at the fact of how the prime-based approach tunes for intervals that one won't be able to use in the original temperament that this temperament is being proxy-tuned for.

5. Determine target-intervals

Regarding our target-interval set, we're still optimizing our tuning for the appropriate TILT here, however, what exactly that TILT includes will be slightly different in this new space. The default max integer is the same, as changing basis hasn't changed our max integer (it would have if our basis's largest integer had been composite, however, such as 33 instead of 11/3!) so we're still asking for a 12-TILT here. But it will be filtered differently. Now we've exchanged our 9 for a 3 in our basis, we're no longer limited to intervals with even counts of prime 3. So we get: {2/1, 3/1 , 3/2, 4/3, 7/3, 7/4, 7/6, 8/3, 9/4, 9/7, 11/4, 11/6, 11/7, 11/8, 11/9, 12/7}. And here's that in matrix form:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{7} \\ \scriptsize{11} \\ \end{array} \end{array} \begin{array} {ccc} \mathrm{T}_L \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {r|r|r|r|r|r|r|r|r|r|r|r|r|r|r|r} 1 & 0 & -1 & 2 & 0 & -2 & -1 & 3 & -2 & 0 & -2 & -1 & 0 & -3 & 0 & 2 \\ 0 & 1 & 1 & -1 & -1 & 0 & -1 & -1 & 2 & 2 & 0 & -1 & 0 & 0 & -2 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 & -1 & 0 & 0 & -1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ \end{array} \right] \end{array} [/math]

We're not bothering with any held-intervals in this tuning scheme, so that's settled already.

As for weights, because we're in a nonprime basis, we don't expect there should be too many surprises here. The actual weight matrix will be too cumbersome to spell out here, since our target-interval count [math]k[/math] is 16. But we will show our [math](4, 4)[/math]-shaped complexity pretransformer, at least, for which there should be no surprises, as it's just like any other one we would have looked at before worrying about nonstandard bases, since all of its elements are primes:

[math] \begin{array} {ccc} \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \\ \\ \\ \\ \end{array} \\ \end{array} \begin{array} {c} \begin{array} {lll} X \\ \end{array} \\ \left[ \begin{array} {c} \log_2{2} & 0 & 0 & 0 \\ 0 & \log_2{3} & 0 & 0 \\ 0 & 0 & \log_2{7} & 0 \\ 0 & 0 & 0 & \log_2{11} \\ \end{array} \right] \\ \end{array} [/math]

6. Optimize

Now for the part we already know how to do: optimize for our generator tuning map [math]𝒈_L[/math], using the mapping from step 4 and the target-interval set from step 5. We should find ⟨1193.102 1891.756 135.810]. As promised, that's three generators, one for each row of our [math]M_L[/math].

7. Convert to tempered-prime tuning map

This generator tuning map is great, but we want to get this optimized tuning information back into our original basis somehow, and we only know how to change the basis for objects that are in terms of primes, and in general, generator tuning maps are not in terms of primes, but of generators. Notice that if we were to write out [math]𝒈_L[/math] in matrix form, we could neither label its row nor its columns with either our original basis or our superspace basis:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \\ \end{array} \end{array} \begin{array} {ccc} 𝒈_L \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {r} 1193.102 & 1891.756 & 135.810 \\ \end{array} \right] \end{array} [/math]

And so that's why — if you were wondering, based on the diagram at the beginning of this exercise — that computing the prime-based tuning requires not just one detour (the one to the comma basis back to a mapping) but two detours: it's the same reason again, just manifesting in a slightly different way, really; we just need to be in a form temporarily where we can accomplish the basis change.

Fortunately, this is an easily solvable problem. We only need to convert our generator tuning map into a prime tuning map (which we usually shorten to simply "tuning map"). And this is as easy as multiplying it by our mapping, which essentially tells us how many of each of these generators it takes to each prime. Multiplying [math]𝒈_LM_L[/math] together, then, we find our tuning map [math]𝒕_L[/math], which equals ⟨1193.102 1891.756 3356.477 4142.150].

8. Return to original basis

Now that we've got our optimized tuning in the basis-change-friendly form of a tuning map [math]𝒕_L[/math], we're ready to change basis back in the other direction, back to our original basis of 2.7/3.11/3. To do this, we right-multiply it by the basis change matrix:

[math] \begin{array} {ccc} 𝒕_L \\ \begin{array} {ccc} \scriptsize{2} &  \scriptsize{3} & \scriptsize{7} &  \scriptsize{11} \\ \end{array} \\ \left[ \begin{array} {rrr} 1193.102 & 1891.756 & 3356.477 & 4142.150 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\large ×} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{3} \\ \scriptsize{7} \\ \scriptsize{11} \\ \end{array} \end{array} \begin{array} {ccc} B_{L↔s} \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{7/3} & \scriptsize{11/3} \\ \end{array} \\ \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & -1 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\huge ⥱} \hspace{0.5cm} \begin{array} {ccc} 𝒕_s \\ \begin{array} {ccc} \scriptsize{2} & \scriptsize{7/3} & \scriptsize{11/3} \\ \end{array} \\ \left[ \begin{array} {rrr} 1193.102 & 1464.722 & 2250.394 \\ \end{array} \right] \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} [/math]

9. Find pseudoinverse

Great. So we're back home, in our original basis. However, we've got our information in the form of a prime tuning map. Maybe that's sufficient for you; if so, you may be excused. For the rest of us who wish to get our actual generator sizes in this temperament tuning, we have a little more work to do.

As you'll recall, we went from generator tuning map [math]𝒈_L[/math] to tempered-prime tuning map [math]𝒕_L[/math] using multiplication, specifically multiplying [math]𝒈_L[/math] by our mapping [math]M_L[/math]. Unfortunately, however, it's not quite so easy to go the other direction, i.e. to extract a [math]𝒈[/math] from a [math]𝒕[/math]; while we do happen to know our [math]M[/math] here, it's not as straightforward as, say, "dividing" a [math]𝒕[/math] by an [math]M[/math] to extract a [math]𝒈[/math]. It is possible, however, but it just requires a bit more cleverness than one might expect.

The key idea is to realize that [math]𝒕 = 𝒈M[/math], and so all we really need to do is right-multiply by something that will cancel out the [math]M[/math] part of it. Such a thing would be called a right-inverse of [math]M[/math], which is to say, something that when [math]M[/math] is right-multiplied by it, we end up with an identity matrix [math]I[/math]. So we don't need a full inverse of [math]M[/math], which would be a matrix that cancels [math]M[/math] out to an identity matrix by either right-multiplication or left-multiplication; and in fact, since any meaningful [math]M[/math] will be rectangular, and rectangular matrices can never have full inverses, it couldn't be. But fortunately for us, since [math]M[/math] is the wide type of rectangular matrix, not tall (i.e. it has more columns than rows), we need look no further for a right-inverse than its pseudoinverse, [math]M^{+}[/math]. That's right: it's the same generalized inverse we have used previously for finding tunings with optimization power [math]p = 2[/math] or interval complexity norm power [math]q = 2[/math]. But it has other convenient uses that have nothing to do with this power of [math]2[/math]. In this case, the math works out so that for wide matrices [math]A[/math], it's the case that [math]AA^{+} = I[/math] (for tall matrices, it's the other way around; [math]A^{+}A = I[/math]).

The pseudoinverse has a simple formula (explained at the link above). Following it, we find:

[math] \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{\frac{7}{3}} \\ \scriptsize{\frac{11}{3}} \\ \end{array} \end{array} \begin{array} {ccc} M^{+}_s \\ \begin{array} {ccc} \end{array} \\ \left[ \begin{array} {rrr} \frac16 & 0 \\ \frac16 & \frac25 \\ \frac13 & -\frac15 \\ \end{array} \right] \end{array} [/math]

Don't be thrown if [math]M^{+}[/math] contains non-integer entries like; it'll still cancel out with [math]M[/math], and it won't make a difference. You may confirm that [math]M_sM^{+}_s = I[/math] if you would like.

10. Convert to generator tuning map

Finally, we can reach our goal of the prime-based TILT minimax-C generator tuning map [math]𝒈_{2.7/3.11/3}[/math], if we just multiply [math]𝒕_s[/math] on the right by [math]M^{+}_s[/math]:

[math] \begin{array} {ccc} 𝒕_s \\ \begin{array} {ccc} \scriptsize{2} &  \scriptsize{\frac73} & \scriptsize{\frac{11}{3}} \\ \end{array} \\ \left[ \begin{array} {rrr} 1193.102 & 1464.722 & 2250.394 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\large ×} \hspace{0.5cm} \begin{array} {ccc} \\ \begin{array} {ccc} \\ \end{array} \\ \begin{array} {rrr} \scriptsize{2} \\ \scriptsize{7/3} \\ \scriptsize{11/3} \\ \end{array} \end{array} \begin{array} {ccc} M^{+}_s \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} \frac16 & 0 \\ \frac16 & \frac25 \\ \frac13 & -\frac15 \\ \end{array} \right] \end{array} \hspace{0.5cm} {\huge ⥱} \hspace{0.5cm} \begin{array} {ccc} 𝒈_s \\ \begin{array} {ccc} \\ \end{array} \\ \left[ \begin{array} {rrr} 1193.102 & 135.801 \\ \end{array} \right] \\ \begin{array} {rrr} \\ \end{array} \\ \end{array} [/math]

That 135.810 ¢ value certainly isn't super close to 116 ¢, the cents size of the purely-tuned [math]\frac{77}{72}[/math] interval for our generator, but hey, it's in the ballpark, certainly for a temperament with as low accuracy as this one.

And so we're done!

See also

Well, you've reached the very end of our article series on RTT tuning. The only place left to go from here is tables. If you'd like to review the conventions for communicating about RTT that we developed over the course of this project, you can behold them in all their centralized glory on this one page: Conventions for names, variables, units, and notations. Otherwise, thanks for your attention, and we hope you got a lot out of this, and will go on to use what you learned to make some excellent music!

Dave: Catch ya later.

Douglas: Happy trails.

We hope you enjoyed reading this series as much as we enjoyed collaborating to write it. 😊 😊

Hey Douglas, shouldn't one of those emoticons have hair?