Dave Keenan & Douglas Blumeyer's guide to RTT: conventions for names, variables, units, and notations

This is an appendix to Dave Keenan & Douglas Blumeyer's guide to RTT, or "D&D's guide" for short. The tables in this article present our recommendations for communicating about regular temperament theory (RTT), in particular the names and notations for temperament matrices, tuning schemes, interval complexities, and measurement units.

Our recommendations are designed to make this topic easy to learn for musicians who do not have technical backgrounds, though we have generally deferred to established mathematical, scientific, and engineering conventions for the benefit of those who do.

For more information on our variation on extended bra-ket notation, please see Extended bra-ket notation: Variant including curly and square brackets.

We've followed a symbol formatting pattern, explained by the table below, which we hope serves as an aid to quickly identifying objects and remembering their properties and purposes, but at the least we hope our choices are unobtrusive. In short, the objects with simple units of primes, generators or cents, i.e. the things which are actually audible in our application, are distinguished by upright formatting, while other variables are italic as is conventional. This is crossed with the mathematical convention that objects of order-1 like vectors are bolded and order-2 like matrices are uppercased:



	units →	simple units	compound or no units
↓ order	↓ style →	upright	italic
0	plain	scalar with simple unit	scalar with no unit
1	bold	vector	map (row vector)
2	UPPERCASE	LIST or BASIS	true MATRIX

We present our conventions here in three separate sections, one for each level of this article series: basic, intermediate, and advanced. The basic section contains only information covered in the basic part of the series, the intermediate section contains both basic and intermediate, and the advanced section contains it all (that is to say, the sections are cumulative)^[1]. We expect that for most readers, the basic tier will be the best reference (this is the reference designed primarily for musicians interested in RTT, as opposed to scientists, engineers, mathematicians, or theoreticians), and so we've left the other two sections initially collapsed.

Basic

Objects


equivalent expressions	variable	name	units			shape		type		EBK notation		subobjects				notes
equivalent expressions	variable	name	unreduced	reduced	read as	unreduced	reduced	numeric	structural	row-first	col-first	row	col	diag	entry	notes
mapping
	[math]\textbf{i}[/math]	(just) interval		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{i}_i[/math]	specific type: vector (prime-count vector or PC-vector) jargon name: monzo
	[math]M[/math]	(temperament) mapping (matrix)		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (r, d)[/math]	integer	matrix	[⟨...] ...}	⟨[...} ...]	[math]𝒎_i[/math]			[math]m_{ij}[/math]	jargon name: val list
[math]M\textbf{i}[/math]	[math]\textbf{y}[/math]	mapped interval	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (r, 1)[/math]	integer	vector		[...}					specific type: generator-count vector (GC-vector) jargon name: tmonzo; mnemonic: [math]\textbf{y}[/math]nterval
	[math]𝒎[/math]	(temperament) map		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (1, d)[/math]	integer	vector	⟨...]					[math]m_i[/math]	jargon name: val
	[math]d[/math]	dimensionality					[math]\scriptsize (1, 1)[/math]	integer	scalar
	[math]r[/math]	rank					[math]\scriptsize (1, 1)[/math]	integer	scalar
tuning
	[math]{\large\textbf{𝓁}}\hspace{2mu}[/math]	log-prime map		[math]\small\mathsf{oct}[/math]/[math]\small 𝗽[/math]	octaves per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]{\large 𝓁}\hspace{2mu}_i[/math]
[math]1200×{\large\textbf{𝓁}}\hspace{2mu}[/math]	[math]𝒋[/math]	just(-prime) tuning map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]j_i[/math]
	[math]𝒈[/math]	generator tuning map		[math]\mathsf{¢}[/math]/[math]\small 𝗴[/math]	cents per generator		[math]\scriptsize (1, r)[/math]	real	vector	{...]					[math]g_i[/math]
[math]𝒈M[/math]	[math]𝒕[/math]	(tempered-prime) tuning map	[math]\scriptsize \begin{array} {c} 𝒈 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗴} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} 𝑀 \\[-2pt] \cancel{𝗴} \hspace{-2mu} / \hspace{-2mu} 𝗽 \end{array} [/math]	[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime	[math]\scriptsize \!\! \begin{array} {c} 𝒈 \\[-3pt] (1, \cancel{r}) \end{array} \!\! \begin{array} {c} M \\[-3pt] (\cancel{r}, d) \end{array} \!\! [/math]	[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]t_i[/math]
[math]𝒕 - 𝒋[/math]	[math]𝒓[/math]	retuning (or mistuning) map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]r_i[/math]	previous name: prime error map
[math]𝒋\textbf{i}[/math]	[math]\mathrm{o}[/math]	(just) (interval) size	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{o}[/math]riginal size
[math]𝒈M\textbf{i} \\ 𝒕\textbf{i}[/math]	[math]\mathrm{a}[/math]	tempered (interval) size	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{a}[/math]ltered size
[math]𝒕\textbf{i} - 𝒋\textbf{i} \\ a - o \\ 𝒓\textbf{i}[/math]	[math]\mathrm{e}[/math]	(interval) error	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar
optimization
	[math]p[/math]	optimization power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]⟪\,·\,⟫_p[/math]	power mean ([math]p[/math]-mean)					[math]\scriptsize (1, 1)[/math]	real	scalar
damage
	[math]c[/math]	complexity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math]^[2]	[math]\small\mathsf{(C)}[/math]	complexity weight		[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\dfrac1c[/math]	[math]s[/math]	simplicity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(S)}[/math]	[math]\small\mathsf{(S)}[/math]	simplicity weight		[math]\scriptsize (1, 1)[/math]	real	scalar
[math]c[/math] or [math]s[/math]	[math]w[/math]	weight	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math] or 𝟙[math]\small\mathsf{(S)}[/math]	[math]\small\mathsf{(C)}[/math] or [math]\small\mathsf{(S)}[/math]	complexity weight or simplicity weight		[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\|\mathrm{e}\|w[/math]	[math]\mathrm{d}[/math]	damage	[math]\scriptsize \begin{array} {c} \|\mathrm{e}\| \\[-2pt] {\small\mathsf{¢}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} w \\[-2pt] \mathsf{(U, C, or\,S)} \end{array} [/math]	[math]\mathsf{¢}\small\mathsf{(U)}[/math] or [math]\mathsf{¢}\small\mathsf{(C)}[/math] or [math]\mathsf{¢}\small\mathsf{(S)}[/math]	(see damages table)	[math]\scriptsize \!\! \begin{array} {c} \|\mathrm{e}\| \\[-3pt] (1, \cancel{1}) \end{array} \!\! \begin{array} {c} w \\[-3pt] (\cancel{1}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar
target-intervals
	[math]\mathrm{T}[/math]	target-interval list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, k)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{t}_i[/math]		[math]\mathrm{t}_{ij}[/math]
[math]M\mathrm{T}[/math]	[math]\mathrm{Y}[/math]	mapped target-interval list	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (r, k)[/math]	integer	matrix		[[...} ...]		[math]\textbf{y}_i[/math]		[math]\mathrm{y}_{ij}[/math]	mnemonic: looks like bent-up 'T', or cross between 'M' and 'T'
[math]𝒋\mathrm{T}[/math]	[math]\textbf{o}[/math]	target-interval (just) size list	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{o}_i[/math]	mnemonic: [math]\textbf{o}[/math]riginal size list
[math]𝒕\mathrm{T} \\ 𝒈M\mathrm{T}[/math]	[math]\textbf{a}[/math]	tempered target-interval size list	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{a}_i[/math]	mnemonic: [math]\textbf{a}[/math]ltered size list
[math]𝒕\mathrm{T} - 𝒋\mathrm{T}\\ \textbf{a} - \textbf{o} \\ 𝒓\mathrm{T} [/math]	[math]\textbf{e}[/math]	target-interval error list	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{e}_i[/math]
[math]C[/math] or [math]S[/math]	[math]W[/math]	target-interval weight matrix	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math] or [math]\small\mathsf{𝟙}\scriptsize\mathsf{(S)}[/math] or [math]\small\mathsf{𝟙}\scriptsize\mathsf{(U)}[/math]	[math]\small\mathsf{(C)}[/math] or [math]\small\mathsf{(S)}[/math] or [math]\small\mathsf{(U)}[/math]	complexity weight or simplicity weight		[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒘[/math]	[math]w_i[/math]
	[math]C[/math]	target-interval complexity weight matrix	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math]	[math]\small\mathsf{(C)}[/math]	complexity weight		[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒄[/math]	[math]c_i[/math]
[math]\dfrac1C[/math]	[math]S[/math]	target-interval simplicity weight matrix	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(S)}[/math]	[math]\small\mathsf{(S)}[/math]	simplicity weight		[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒔[/math]	[math]s_i[/math]	entrywise reciprocal of [math]C[/math]
[math]\|\textbf{e}\|W[/math]	[math]\textbf{d}[/math]	target-interval damage list^[3]	[math]\scriptsize \begin{array} {c} \|\textbf{e}\| \\[-2pt] {\small\mathsf{¢}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} W \\[-2pt] (\mathsf{U, C, or\,S}) \end{array} [/math]	[math]\mathsf{¢}\small\mathsf{(U)}[/math], [math]\mathsf{¢}\small\mathsf{(C)}[/math], or [math]\mathsf{¢}\small\mathsf{(S)}[/math]	weighted cents	[math]\scriptsize \!\! \begin{array} {c} \|\textbf{e}\| \\[-3pt] (1, \cancel{k}) \end{array} \!\! \begin{array} {c} W \\[-3pt] (\cancel{k}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{d}_i[/math]
	[math]k[/math]	target-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar							mnemonic: [math]k[/math]ount
held-intervals
	[math]\mathrm{H}[/math]	held-interval basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, h)[/math]		matrix		[[...⟩ ...]		[math]\textbf{h}_i[/math]		[math]\mathrm{h}_{ij}[/math]
	[math]h[/math]	held-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar
exploring temperaments
	[math]\mathrm{C}[/math]	comma basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, n)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{c}_i[/math]		[math]\mathrm{c}_{ij}[/math]	jargon name: monzo list
	[math]\textbf{c}[/math]	comma		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{c}_i[/math]	specific type: vector (prime-count vector or PC-vector)

Units

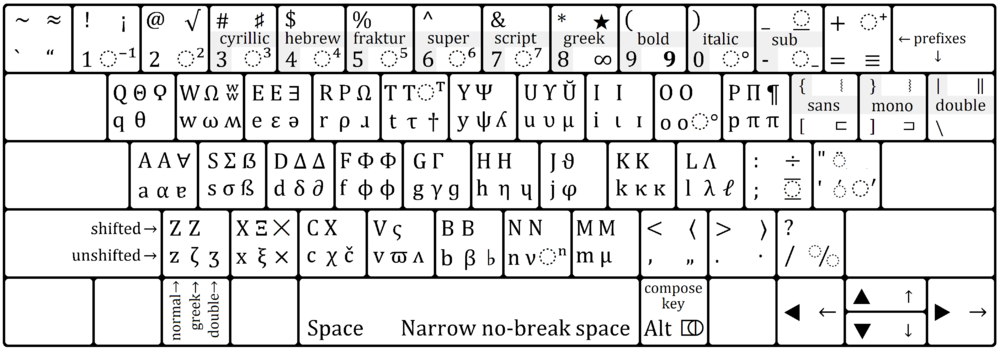
We recommend using a narrow no-break space (U+202F) between quantities and their units.^[4] For how to type this, see the WinCompose section below.


symbol	name	vectorized
[math]\small 𝗴[/math]	generators	yes
[math]\small 𝗽[/math]	primes	yes
[math]\mathsf{¢}[/math]^[5]	cents
[math]\mathsf{¢}\small\mathsf{(U)}[/math]	unity-weighted cents
[math]\mathsf{¢}\small\mathsf{(C)}[/math]	complexity-weighted cents
[math]\mathsf{¢}\small\mathsf{(S)}[/math]	simplicity-weighted cents
[math]\small\mathsf{oct}[/math]	octaves
[math]\small\mathsf{(C)}[/math]	complexity weight
[math]\small\mathsf{(S)}[/math]	simplicity weight

Tuning schemes

Copied from Dave Keenan & Douglas Blumeyer's guide to RTT: tuning fundamentals#Systematic tuning scheme names.


damage weight	optimization power	systematic name
<none>	∞	minimax-U
complexity		minimax-C
1/complexity		minimax-S
<none>	2	miniRMS-U
complexity		miniRMS-C
1/complexity		miniRMS-S
<none>	1	miniaverage-U
complexity		miniaverage-C
1/complexity		miniaverage-S

Damages


quantity		unit
abbreviation	name	symbol	name
U-damage	unity-weight damage	[math]\mathsf{¢}\small\mathsf{(U)}[/math]	unity-weighted cents
C-damage	complexity-weight damage	[math]\mathsf{¢}\small\mathsf{(C)}[/math]	complexity-weighted cents
S-damage	simplicity-weight damage	[math]\mathsf{¢}\small\mathsf{(S)}[/math]	simplicity-weighted cents

Complexity and simplicity


quantity		unit
abbreviation	name	symbol	name
C	complexity	[math]\small\mathsf{(C)}[/math]	complexity weight
S	simplicity	[math]\small\mathsf{(S)}[/math]	simplicity weight

[math] % \slant{} command approximates italics to allow slanted bold characters, including digits, in MathJax. \def\slant#1{\style{display:inline-block;margin:-.05em;transform:skew(-14deg)translateX(.03em)}{#1}} % Latex equivalents of the wiki templates llzigzag and rrzigzag for double zigzag brackets. \def\llzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}} \def\rrzigzag{\hspace{-1.6mu}\style{display:inline-block;transform:scale(-.62,1.24)translateY(.07em);font-family:sans-serif}{ꗨ\hspace{-3mu}ꗨ}\hspace{-1.6mu}} [/math]

Intermediate

Objects


equivalent expressions	variable	name	units			shape		type		EBK notation		subobjects				notes
equivalent expressions	variable	name	unreduced	reduced	read as	unreduced	reduced	numeric	structural	row-first	col-first	row	col	diag	entry	notes
mapping
	[math]\textbf{i}[/math]	(just) interval		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{i}_i[/math]	specific type: vector (prime-count vector or PC-vector) jargon name: monzo
	[math]M[/math]	(temperament) mapping (matrix)		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (r, d)[/math]	integer	matrix	[⟨...] ...}	⟨[...} ...]	[math]𝒎_i[/math]			[math]m_{ij}[/math]	jargon name: val list
[math]M\textbf{i}[/math]	[math]\textbf{y}[/math]	mapped interval	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (r, 1)[/math]	integer	vector		[...}					specific type: generator-count vector (GC-vector) jargon name: tmonzo; mnemonic: [math]\textbf{y}[/math]nterval
	[math]𝒎[/math]	(temperament) map		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (1, d)[/math]	integer	vector	⟨...]					[math]m_i[/math]	jargon name: val
[math]n + r[/math]	[math]d[/math]	dimensionality					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]d - n[/math]	[math]r[/math]	rank					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]d - r[/math]	[math]n[/math]	nullity					[math]\scriptsize (1, 1)[/math]	integer	scalar
tuning
	[math]{\large\textbf{𝓁}}\hspace{2mu}[/math]	log-prime map		[math]\small\mathsf{oct}[/math]/[math]\small 𝗽[/math]	octaves per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]{\large 𝓁}\hspace{2mu}_i[/math]
[math]1200×{\large\textbf{𝓁}}\hspace{2mu}[/math]	[math]𝒋[/math]	just(-prime) tuning map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]j_i[/math]
	[math]𝒈[/math]	generator tuning map		[math]\mathsf{¢}[/math]/[math]\small 𝗴[/math]	cents per generator		[math]\scriptsize (1, r)[/math]	real	vector	{...]					[math]g_i[/math]
	[math]𝒕[/math]	(tempered-prime) tuning map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]t_i[/math]
[math]𝒕 - 𝒋 \\ 1200×\slant{\mathbf{1}}L(P - I)[/math]	[math]𝒓[/math]	retuning (or mistuning) map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]r_i[/math]	previous name: prime error map
[math]𝒋\textbf{i}[/math]	[math]\mathrm{o}[/math]	(just) (interval) size	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{o}[/math]riginal size
[math]𝒈M\textbf{i} \\ 𝒕\textbf{i}[/math]	[math]\mathrm{a}[/math]	tempered (interval) size	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{a}[/math]ltered size
[math]𝒕\textbf{i} - 𝒋\textbf{i} \\ a - o \\ 𝒓\textbf{i}[/math]	[math]\mathrm{e}[/math]	(interval) error	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar
optimization
	[math]p[/math]	optimization power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]⟪\,·\,⟫_p[/math]	power mean ([math]p[/math]-mean)					[math]\scriptsize (1, 1)[/math]	real	scalar
damage
	[math]c[/math]	complexity	(see complexities section of complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\dfrac1c[/math]	[math]s[/math]	simplicity	(see simplicities section of complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]c[/math] or [math]s[/math]	[math]w[/math]	weight	(see complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\|\mathrm{e}\|w[/math]	[math]\mathrm{d}[/math]	damage	(see damages table)				[math]\scriptsize (1, 1)[/math]	real	scalar
target-intervals
	[math]\mathrm{T}[/math]	target-interval list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, k)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{t}_i[/math]		[math]\mathrm{t}_{ij}[/math]
[math]M\mathrm{T}[/math]	[math]\mathrm{Y}[/math]	mapped target-interval list	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (r, k)[/math]	integer	matrix		[[...} ...]		[math]\textbf{y}_i[/math]		[math]\mathrm{y}_{ij}[/math]	mnemonic: looks like bent-up 'T', or cross between 'M' and 'T'
[math]𝒋\mathrm{T}[/math]	[math]\textbf{o}[/math]	target-interval (just) size list	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{o}_i[/math]	mnemonic: [math]\textbf{o}[/math]riginal size list
[math]𝒕\mathrm{T}[/math]	[math]\textbf{a}[/math]	tempered target-interval size list	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{a}_i[/math]	mnemonic: [math]\textbf{a}[/math]ltered size list
[math]𝒕\mathrm{T} - 𝒋\mathrm{T} \\ 𝒓\mathrm{T} \\ \textbf{a} - \textbf{o}[/math]	[math]\textbf{e}[/math]	target-interval error list	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{e}_i[/math]
[math]C[/math] or [math]S[/math]	[math]W[/math]	target-interval weight matrix	(see complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒘[/math]	[math]w_i[/math]
	[math]C[/math]	target-interval complexity weight matrix	(see complexities section of complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒄[/math]	[math]c_i[/math]
[math]\dfrac1C[/math]	[math]S[/math]	target-interval simplicity weight matrix	(see simplicities section of complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒔[/math]	[math]s_i[/math]	entrywise reciprocal of [math]C[/math]
[math]\|\textbf{e}\|W[/math]	[math]\textbf{d}[/math]	target-interval damage list	(see damages table)				[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{d}_i[/math]
	[math]k[/math]	target-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar							mnemonic: [math]k[/math]ount
held-intervals
	[math]\mathrm{H}[/math]	held-interval basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, h)[/math]		matrix		[[...⟩ ...]		[math]\textbf{h}_i[/math]		[math]\mathrm{h}_{ij}[/math]
	[math]h[/math]	held-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar
exploring temperaments
	[math]\mathrm{C}[/math]	comma basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, n)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{c}_i[/math]		[math]\mathrm{c}_{ij}[/math]	jargon name: monzo list
	[math]\textbf{c}[/math]	comma		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{c}_i[/math]	specific type: vector (prime-count vector or PC-vector)
computation
	[math]\llzigzag·\,\rrzigzag\!_p[/math]	power sum ([math]p[/math]-sum)					[math]\scriptsize (1, 1)[/math]	real	scalar
all-interval tuning schemes
[math]\mathrm{I}[/math]	[math]\mathrm{T}_{\text{p}}[/math]	prime proxy target-interval list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, d)[/math]	integer	matrix		⟨[...⟩ ...]			[math]\mathbf{1}[/math]
	[math]X[/math]	complexity prescaler	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math]	[math]\small\mathsf{(C)}[/math]	complexity weight		[math]\scriptsize (d, d)[/math]	real	matrix	[⟨...] ...⟩				[math]𝒙[/math]	[math]x_i[/math]
[math]\text{diag}({\large\textbf{𝓁}}\hspace{2mu})[/math]	[math]L[/math]	log-prime matrix		[math]\small\mathsf{oct}[/math]/[math]\small 𝗽[/math]	octaves per prime		[math]\scriptsize (d, d)[/math]	real	matrix	[⟨...] ...⟩	⟨[...⟩ ...]	[math]{\large\textbf{𝓁}}\hspace{2mu}_i[/math]		[math]{\large\textbf{𝓁}}\hspace{2mu}[/math]	[math]{\large 𝓁}\hspace{2mu}_{ij}[/math]
	[math]q[/math]	interval complexity norm power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖ · ‖_q[/math]	power norm ([math]p[/math]-norm)					[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\dfrac1{1-\frac1q}[/math]	[math]\text{dual}(q)[/math]	dual norm power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖X\mathbf{i}‖_q[/math]	interval complexity		[math]\small\mathsf{(C)}[/math]			[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖𝒓X^{-1}‖_{\text{dual}(q)}[/math]	retuning magnitude		[math]\mathsf{¢}\small\mathsf{(C^{-1})}[/math]			[math]\scriptsize (1, 1)[/math]	real	scalar

Units

Same as the basic level.

Tuning schemes


retuning (or mistuning) magnitude			damage									target intervals	systematic name		previously named tuning schemes that are specific types of this tuning scheme	of interest?
			weight						optimization
			interval complexity			slope			initial	name	power
initial	name	power	initial	name	power	initial	name	multiplier	initial	name	power		abbreviated	read ("____ tuning scheme")
<n/a>	maximum	∞	(t)	taxicab	1	S	simplicity-weight	1/complexity	<n/a>	minimax	∞	all	minimax-S	minimax simplicity-weight damage	"TOP"/"T1"/"TIPTOP", "CTOP", "POTOP"/"POTT", "BOP", "Weil", "Kees"	yes
<n/a>	Euclidean	2	E	Euclidean	2	S	simplicity-weight	1/complexity				all	minimax-ES	minimax Euclideanized-simplicity-weight damage	"TE"/"T2"/"TOP-RMS", "CTE", "POTE", "Frobenius", "BE", "WE", "KE"
<n/a>			<n/a>			U	unity-weight	<none>				<set>	<set> minimax-U	<set> minimax unity-weight-damage	"minimax"	yes
			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> minimax-S	<set> minimax simplicity-weight damage		yes
			E	Euclidean	2	S	simplicity-weight	1/complexity					<set> minimax-ES	<set> minimax Euclideanized-simplicity-weight damage
			(t)	taxicab	1	C	complexity-weight	complexity					<set> minimax-C	<set> minimax complexity-weight damage		yes
			E	Euclidean	2	C	complexity-weight	complexity					<set> minimax-EC	<set> minimax Euclideanized-complexity-weight damage
			<n/a>			U	unity-weight	<none>		miniRMS	2		<set> miniRMS-U	<set> miniRMS unity-weight damage	"least squares"	yes
			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> miniRMS-S	<set> miniRMS simplicity-weight damage		yes
			E	Euclidean	2	S	simplicity-weight	1/complexity					<set> miniRMS-ES	<set> miniRMS Euclideanized-simplicity-weight damage
			(t)	taxicab	1	C	complexity-weight	complexity					<set> miniRMS-C	<set> miniRMS complexity-weight damage		yes
			E	Euclidean	2	C	complexity-weight	complexity					<set> miniRMS-EC	<set> miniRMS Euclideanized-complexity-weight damage
			<n/a>			U	unity-weight	<none>		miniaverage	1		<set> miniaverage-U	<set> miniaverage unity-weight damage		yes
			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> miniaverage-S	<set> miniaverage simplicity-weight damage		yes
			E	Euclidean	2	S	simplicity-weight	1/complexity					<set> miniaverage-ES	<set> miniaverage Euclideanized-simplicity-weight damage
			(t)	taxicab	1	C	complexity-weight	complexity					<set> miniaverage-C	<set> miniaverage complexity-weight damage		yes
			E	Euclidean	2	C	complexity-weight	complexity					<set> miniaverage-EC	<set> miniaverage Euclideanized-complexity-weight damage

Damages


quantity		unit
abbreviation	name	symbol	name
U-damage	unity-weight damage	[math]\mathsf{¢}\small\mathsf{(U)}[/math]	unity-weighted cents
C-damage	complexity-weight damage	[math]\mathsf{¢}\small\mathsf{(C)}[/math]	complexity-weighted cents
EC-damage	Euclideanized-complexity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(EC)}[/math]	Euclideanized-complexity-weighted cents
S-damage	simplicity-weight damage	[math]\mathsf{¢}\small\mathsf{(S)}[/math]	simplicity-weighted cents
ES-damage	Euclideanized-simplicity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(ES)}[/math]	Euclideanized-simplicity-weighted cents

Complexity and simplicity


quantity		unit
abbreviation	name	symbol	name
C	complexity	[math]\small\mathsf{(C)}[/math]	complexity weight
EC	Euclideanized complexity	[math]\small\mathsf{(EC)}[/math]	Euclideanized-complexity weight
S	simplicity	[math]\small\mathsf{(S)}[/math]	simplicity weight
ES	Euclideanized simplicity	[math]\small\mathsf{(ES)}[/math]	Euclideanized-simplicity weight

Advanced

Objects


equivalent expressions	variable	name	units			shape		type		EBK notation		subobjects				notes
equivalent expressions	variable	name	unreduced	reduced	read as	unreduced	reduced	numeric	structural	row-first	col-first	row	col	diag	entry	notes
mapping
	[math]\textbf{i}[/math]	(just) interval		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{i}_i[/math]	specific type: vector (prime-count vector or PC-vector) jargon name: monzo
	[math]M[/math]	(temperament) mapping (matrix)		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (r, d)[/math]	integer	matrix	[⟨...] ...}	⟨[...} ...]	[math]𝒎_i[/math]			[math]m_{ij}[/math]	jargon name: val list
[math]M\textbf{i}[/math]	[math]\textbf{y}[/math]	mapped interval	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (r, 1)[/math]	integer	vector		[...}					specific type: generator-count vector (GC-vector) jargon name: tmonzo; mnemonic: [math]\textbf{y}[/math]nterval
	[math]𝒎[/math]	(temperament) map		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (1, d)[/math]	integer	vector	⟨...]					[math]m_i[/math]	jargon name: val
[math]n + r[/math]	[math]d[/math]	dimensionality					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]d - n[/math]	[math]r[/math]	rank					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]d - r[/math]	[math]n[/math]	nullity					[math]\scriptsize (1, 1)[/math]	integer	scalar
tuning
[math]\slant{\mathbf{1}}L[/math]	[math]{\large\textbf{𝓁}}\hspace{2mu}[/math]	log-prime map		[math]\small\mathsf{oct}[/math]/[math]\small 𝗽[/math]	octaves per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]{\large 𝓁}\hspace{2mu}_i[/math]
[math]1200×\slant{\mathbf{1}}LG_{\text{j}}M_{\text{j}} \\ 1200×\slant{\mathbf{1}}L \\ 𝒈_{\text{j}}M_{\text{j}}[/math]	[math]𝒋[/math]	just(-prime) tuning map	[math]\scriptsize \begin{array} {c} 1200 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \slant{\mathbf{1}} \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} L \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \\ \scriptsize \quad \begin{array} {c} G_{\text{j}} \\[-2pt] \cancel{𝗽} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗴} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} M_{\text{j}} \\[-2pt] \cancel{𝗴} \hspace{-2mu} / \hspace{-2mu} 𝗽 \end{array} [/math]	[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime	[math]\scriptsize \!\! \begin{array} {c} 1200 \\[-3pt] (1, \cancel{1}) \end{array} \!\! \begin{array} {c} \slant{\mathbf{1}} \\[-3pt] (\cancel{1}, \cancel{d}) \end{array} \!\! \begin{array} {c} L \\[-3pt] (\cancel{d}, \cancel{d}) \end{array} \\ \scriptsize \quad \!\! \begin{array} {c} G_{\text{j}} \\[-3pt] (\cancel{d}, \cancel{r}) \end{array} \!\! \begin{array} {c} M_{\text{j}} \\[-3pt] (\cancel{r}, d) \end{array} \!\! [/math]	[math]\scriptsize (1, d_{\text{p}})[/math]	real	vector	⟨...]					[math]j_i[/math]
[math]1200×\slant{\mathbf{1}}LG[/math]	[math]𝒈[/math]	generator tuning map	[math]\scriptsize \begin{array} {c} 1200 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \slant{\mathbf{1}} \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} L \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \\ \scriptsize \quad \begin{array} {c} G \\[-2pt] \cancel{𝗽} \hspace{-2mu} / \hspace{-2mu} 𝗴 \end{array} [/math]	[math]\mathsf{¢}[/math]/[math]\small 𝗴[/math]	cents per generator	[math]\scriptsize \!\! \begin{array} {c} 1200 \\[-3pt] (1, \cancel{1}) \end{array} \!\! \begin{array} {c} \slant{\mathbf{1}} \\[-3pt] (\cancel{1}, \cancel{d}) \end{array} \!\! \begin{array} {c} L \\[-3pt] (\cancel{d}, \cancel{d}) \end{array} \\ \scriptsize \quad \!\! \begin{array} {c} G \\[-3pt] (\cancel{d}, r) \end{array} \!\! [/math]	[math]\scriptsize (1, r)[/math]	real	vector	{...]					[math]g_i[/math]
[math]1200×\slant{\mathbf{1}}LGM \\ 1200×\slant{\mathbf{1}}LP \\ 𝒈M[/math]	[math]𝒕[/math]	(tempered-prime) tuning map	[math]\scriptsize \begin{array} {c} 1200 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \slant{\mathbf{1}} \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{\mathsf{oct}} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} L \\[-2pt] \cancel{\mathsf{oct}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \\ \scriptsize \quad \begin{array} {c} G \\[-2pt] \cancel{𝗽} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗴} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} M \\[-2pt] \cancel{𝗴} \hspace{-2mu} / \hspace{-2mu} 𝗽 \end{array} [/math]	[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime	[math]\scriptsize \!\! \begin{array} {c} 1200 \\[-3pt] (1, \cancel{1}) \end{array} \!\! \begin{array} {c} \slant{\mathbf{1}} \\[-3pt] (\cancel{1}, \cancel{d}) \end{array} \!\! \begin{array} {c} L \\[-3pt] (\cancel{d}, \cancel{d}) \end{array} \\ \scriptsize \quad \!\! \begin{array} {c} G \\[-3pt] (\cancel{d}, \cancel{r}) \end{array} \!\! \begin{array} {c} M \\[-3pt] (\cancel{r}, d) \end{array} \!\! [/math]	[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]t_i[/math]
[math]𝒕 - 𝒋 \\ 1200×\slant{\mathbf{1}}L(P - I)[/math]	[math]𝒓[/math]	retuning (or mistuning) map		[math]\mathsf{¢}[/math]/[math]\small 𝗽[/math]	cents per prime		[math]\scriptsize (1, d)[/math]	real	vector	⟨...]					[math]r_i[/math]	previous name: prime error map
[math]𝒋\textbf{i}[/math]	[math]\mathrm{o}[/math]	(just) (interval) size	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{o}[/math]riginal size
[math]𝒈M\textbf{i} \\ 𝒕\textbf{i}[/math]	[math]\mathrm{a}[/math]	tempered (interval) size	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar							mnemonic: [math]\mathrm{a}[/math]ltered size
[math]𝒕\textbf{i} - 𝒋\textbf{i} \\ a - o \\ 𝒓\textbf{i}[/math]	[math]\mathrm{e}[/math]	(interval) error	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (1, 1)[/math]	real	scalar
optimization
	[math]p[/math]	optimization power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]⟪\,·\,⟫_p[/math]	power mean ([math]p[/math]-mean)					[math]\scriptsize (1, 1)[/math]	real	scalar
damage
	[math]c[/math]	complexity	(see complexities section of complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\dfrac1c[/math]	[math]s[/math]	simplicity	(see simplicities section of complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]c[/math] or [math]s[/math]	[math]w[/math]	weight	(see complexities and simplicities table)				[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\|\mathrm{e}\|w[/math]	[math]\mathrm{d}[/math]	damage	(see damages table)				[math]\scriptsize (1, 1)[/math]	real	scalar
target-intervals
	[math]\mathrm{T}[/math]	target-interval list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, k)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{t}_i[/math]		[math]\mathrm{t}_{ij}[/math]
[math]M\mathrm{T}[/math]	[math]\mathrm{Y}[/math]	mapped target-interval list	[math]\scriptsize \begin{array} {c} M \\[-2pt] 𝗴 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗴[/math]	generators	[math]\scriptsize \!\! \begin{array} {c} M \\[-3pt] (r, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (r, k)[/math]	integer	matrix		[[...} ...]		[math]\textbf{y}_i[/math]		[math]\mathrm{y}_{ij}[/math]	mnemonic: looks like bent-up 'T', or cross between 'M' and 'T'
[math]𝒋\mathrm{T}[/math]	[math]\textbf{o}[/math]	target-interval (just) size list	[math]\scriptsize \begin{array} {c} 𝒋 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒋 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{o}_i[/math]	mnemonic: [math]\textbf{o}[/math]riginal size list
[math]𝒕\mathrm{T}[/math]	[math]\textbf{a}[/math]	tempered target-interval size list	[math]\scriptsize \begin{array} {c} 𝒕 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒕 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{a}_i[/math]	mnemonic: [math]\textbf{a}[/math]ltered size list
[math]𝒕\mathrm{T} - 𝒋\mathrm{T} \\ 𝒓\mathrm{T} \\ \textbf{a} - \textbf{o}[/math]	[math]\textbf{e}[/math]	target-interval error list	[math]\scriptsize \begin{array} {c} 𝒓 \\[-2pt] {\small\mathsf{¢}} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \mathrm{T} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\mathsf{¢}[/math]	cents	[math]\scriptsize \!\! \begin{array} {c} 𝒓 \\[-3pt] (1, \cancel{d}) \end{array} \!\! \begin{array} {c} \mathrm{T} \\[-3pt] (\cancel{d}, k) \end{array} \!\! [/math]	[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{e}_i[/math]
[math]C[/math] or [math]S[/math]	[math]W[/math]	target-interval weight matrix	(see complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒘[/math]	[math]w_i[/math] or [math]w_{ij}[/math]
	[math]C[/math]	target-interval complexity weight matrix	(see complexities section of complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒄[/math]	[math]c_i[/math]
[math]\dfrac1C[/math]	[math]S[/math]	target-interval simplicity weight matrix	(see simplicities section of complexities and simplicities table)				[math]\scriptsize (k, k)[/math]	real	matrix		[[...] ...]			[math]𝒔[/math]	[math]s_i[/math]	entrywise reciprocal of [math]C[/math]
[math]\|\textbf{e}\|W \\ 1200×\slant{\mathbf{1}}L\|P - I\|\mathrm{T}W[/math]	[math]\textbf{d}[/math]	target-interval damage list	(see damages table)				[math]\scriptsize (1, k)[/math]	real	list	[...]					[math]\mathrm{d}_i[/math]
	[math]k[/math]	target-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar							mnemonic: [math]k[/math]ount
held-intervals
	[math]\mathrm{H}[/math]	held-interval basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, h)[/math]		matrix		[[...⟩ ...]		[math]\textbf{h}_i[/math]		[math]\mathrm{h}_{ij}[/math]
	[math]h[/math]	held-interval count					[math]\scriptsize (1, 1)[/math]	integer	scalar
exploring temperaments
	[math]\mathrm{C}[/math]	comma basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, n)[/math]	integer	matrix		[[...⟩ ...]		[math]\textbf{c}_i[/math]		[math]\mathrm{c}_{ij}[/math]	jargon name: monzo list
	[math]\textbf{c}[/math]	comma		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, 1)[/math]	integer	vector		[...⟩				[math]\mathrm{c}_i[/math]	specific type: vector (prime-count vector or PC-vector)
computation
	[math]\llzigzag·\,\rrzigzag\!_p[/math]	power sum ([math]p[/math]-sum)					[math]\scriptsize (1, 1)[/math]	real	scalar
all-interval tuning schemes
[math]\mathrm{I}[/math]	[math]\mathrm{T}_{\text{p}}[/math]	prime proxy target-interval list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, d)[/math]	integer	matrix		⟨[...⟩ ...]			[math]\slant{\mathbf{1}}[/math]
	[math]X[/math]	complexity pretransformer	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math] or [math]\small\mathsf{𝟙}\scriptsize\mathsf{(}[/math]<alt>-[math]\scriptsize\mathsf{C)}[/math]^[6]	[math]\small\mathsf{(C)}[/math] or [math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{C)}[/math]	complexity weight or <alternative>-complexity weight		[math]\scriptsize (d, d)[/math] or [math]\scriptsize (d+1, d+1)[/math]	real	matrix	[⟨...] ...⟩		[math]𝒙_i[/math]		[math]𝒙[/math]	[math]x_i[/math] or [math]x_{ij}[/math]
[math]\text{diag}({\large\textbf{𝓁}}\hspace{2mu})[/math]	[math]L[/math]	log-prime matrix		[math]\small\mathsf{oct}[/math]/[math]\small 𝗽[/math]	octaves per prime		[math]\scriptsize (d, d)[/math]	real	matrix	[⟨...] ...⟩	⟨[...⟩ ...]	[math]{\large\textbf{𝓁}}\hspace{2mu}_i[/math]		[math]{\large\textbf{𝓁}}\hspace{2mu}[/math]	[math]{\large 𝓁}\hspace{2mu}_{ij}[/math]
	[math]q[/math]	interval complexity norm power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖ · ‖_q[/math]	power norm ([math]p[/math]-norm)					[math]\scriptsize (1, 1)[/math]	real	scalar
[math]\dfrac1{1-\frac1q}[/math]	[math]\text{dual}(q)[/math]	dual norm power					[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖X\mathbf{i}‖_q[/math]	interval complexity		[math]\small\mathsf{(C)}[/math] or [math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{C)}[/math]			[math]\scriptsize (1, 1)[/math]	real	scalar
	[math]‖𝒓X^{-1}‖_{\text{dual}(q)}[/math]	retuning magnitude		[math]\mathsf{¢}\small\mathsf{(C^{-1})}[/math] or [math]\mathsf{¢}\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{C^{-1})}[/math]			[math]\scriptsize (1, 1)[/math]	real	scalar
alternative complexities
	[math]𝒑[/math]	prime list^[7]					[math]\scriptsize (1, d)[/math]	integer	list	[...]					[math]p_i[/math]
	[math]\slant{\mathbf{1}}[/math]	summation map					[math]\scriptsize (1, d)[/math]	integer	vector	⟨...]					[math]1[/math]
	[math]1200[/math]	octaves-to-cents conversion		¢/oct	cents per octave		[math]\scriptsize (1, 1)[/math]	integer	scalar
	[math]Z[/math]	size-sensitizing matrix					[math]\scriptsize (d+1, d)[/math]	real	matrix	[⟨…]...]		[math]𝒛_i[/math]			[math]z_{ij}[/math]
non-standard domain bases
	[math]B_s[/math]	(domain) basis (change) matrix		[math]\small 𝗽[/math]/[math]\small 𝗯[/math]	primes per nonprime basis elements		[math]\scriptsize (d_p, d_b)[/math]	integer	matrix	[[...] ...]	[[...] ...]		[math]b_i[/math]		[math]b_{ij}[/math]
	[math]B_{Ls}[/math]	(domain) basis (change) matrix		[math]\small 𝗕[/math]/[math]\small 𝗯[/math]	superspace basis elements per (subspace) basis elements		[math]\scriptsize (d_L, d_s)[/math]	integer	matrix	[[...] ...]	[[...] ...]		[math]b_i[/math]		[math]b_{ij}[/math]
embedding and projection
	[math]G[/math]	generator embedding (matrix)		[math]\small 𝗽[/math]/[math]\small 𝗴[/math]	primes per generator		[math]\scriptsize (d, r)[/math]	real	matrix	[{...] ...⟩	{[...⟩ ...]	[math]𝒈_i[/math]			[math]g_{ij}[/math]
[math]G_cF^{-1}FM_c \\ \mathrm{V}\textit{Λ}\mathrm{V}^{-1}[/math]	[math]P[/math]	projection (matrix)	[math]\scriptsize \begin{array} {c} G \\[-2pt] 𝗽 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗴} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} M \\[-2pt] \cancel{𝗴} \hspace{-2mu} / \hspace{-2mu} 𝗽 \end{array} [/math]	[math]\small 𝗽[/math]/[math]\small 𝗽[/math]	primes per prime	[math]\scriptsize \!\! \begin{array} {c} G \\[-3pt] (d, \cancel{r}) \end{array} \!\! \begin{array} {c} M \\[-3pt] (\cancel{r}, d) \end{array} \!\! [/math]	[math]\scriptsize (d, d)[/math]	real	matrix	[⟨...] ...⟩	⟨[...⟩ ...]	[math]𝒑_i[/math]			[math]p_i[/math]
[math]GM\textbf{i}[/math]	[math]P\textbf{i}[/math]	projected interval	[math]\scriptsize \begin{array} {c} G \\[-2pt] 𝗽 \hspace{-2mu} / \hspace{-2mu} \cancel{𝗴} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} M \\[-2pt] \cancel{𝗴} \hspace{-2mu} / \hspace{-2mu} \cancel{𝗽} \end{array} \begin{array} {c} \\[-2pt] · \end{array} \begin{array} {c} \textbf{i} \\[-2pt] \cancel{𝗽} \end{array} [/math]	[math]\small 𝗽[/math]	primes	[math]\scriptsize \!\! \begin{array} {c} G \\[-3pt] (d, \cancel{r}) \end{array} \!\! \begin{array} {c} M \\[-3pt] (\cancel{r}, \cancel{d}) \end{array} \!\! \begin{array} {c} \textbf{i} \\[-3pt] (\cancel{d}, 1) \end{array} \!\! [/math]	[math]\scriptsize (d, 1)[/math]	real	vector		[...⟩					specific type: vector (prime-count vector or PC-vector)
	[math]\mathrm{U}[/math]	unchanged-interval basis		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, r)[/math]		matrix		[[...⟩ ...]		[math]\textbf{u}_i[/math]		[math]\mathrm{u}_{ij}[/math]	jargon name: eigenmonzo list
	[math]\textit{Λ}[/math]	scaling factor (eigenvalue) matrix					[math]\scriptsize (d, d)[/math]		matrix	[⟨…] …⟩	⟨[…⟩ …]			[math]𝝀[/math]	[math]λ_i[/math]	mnemonic: [math]\mathrm{V}[/math] is mirrored of [math]\textit{Λ}[/math] which it combines with to create the projection matrix; previous name: eigenvalue matrix
	[math]\mathrm{V}[/math]	unrotated vector (eigenvector) list		[math]\small 𝗽[/math]	primes		[math]\scriptsize (d, d)[/math]		matrix		⟨[...⟩ ...]		[math]\textbf{v}_i[/math]		[math]\mathrm{v}_{ij}[/math]	mnemonic: [math]\mathrm{V}[/math] is mirrored of [math]\textit{Λ}[/math] which it combines with to create the projection matrix; jargon name: eigenmonzo and comma list
	[math]F[/math]	generator form matrix					[math]\scriptsize (r, r)[/math]		matrix	[{...] …}			[math]𝒇_i[/math]		[math]f_{ij}[/math]
[math]I[/math]	[math]M_{\text{j}}[/math]	JI mapping (matrix)		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (d, d)[/math]	integer	matrix	[⟨...] ...}	⟨[...} ...]			[math]\slant{\mathbf{1}}[/math]
[math]I[/math]	[math]G_{\text{j}}[/math]	JI generator embedding (matrix)		[math]\small 𝗽[/math]/[math]\small 𝗴[/math]	primes per generator		[math]\scriptsize (d, d)[/math]	integer	matrix	[{...] ...⟩	{[...⟩ ...]			[math]\slant{\mathbf{1}}[/math]
	[math]K[/math]	constraint (matrix)					[math]\scriptsize (k, r)[/math]	[math]\scriptsize \{0, +1, -1\}[/math]	matrix	[[...] ...]		[math]𝒌_i[/math]			[math]k_{ij}[/math]	mnemonic: [math]K[/math]onstraint
	[math]𝒃[/math]	(generator tuning map) blend map					[math]\scriptsize (1, τ-1)[/math]	real	vector	[...]					[math]b_i[/math]
	[math]B[/math]	(generator tuning map) blend matrix					[math]\scriptsize (d, τ-1)[/math]	real	matrix	[[...⟩...]			[math]𝒃_{i}[/math]		[math]b_{ij}[/math]
	[math]D[/math]	(generator tuning map) deltas matrix		[math]\mathsf{¢}[/math]/[math]\small 𝗴[/math]	cents per generator		[math]\scriptsize (τ-1,r)[/math]	real	matrix	[{...] ...]		[math]𝜹_i[/math]			[math]𝛿_{ij}[/math]
	[math]τ[/math]	tied basic minimax tuning count						integer	scalar
exterior algebra
	[math]𝕞[/math]	multimap		[math]\small 𝗴[/math]/[math]\small 𝗽[/math]	generators per prime		[math]\scriptsize (1, d)[/math]	integer	multivector	⟨...] or ⟨⟨...]] or ⟨⟨⟨...]]] ...					[math]𝕞_i[/math]
	[math]𝕔[/math]	multicomma		[math]\small 𝗽[/math]	primes		[math]\scriptsize (1, n)[/math]	integer	multivector		[...⟩ or [[...⟩⟩ or [[[...⟩⟩⟩ ...				[math]𝕔_i[/math]
	[math]𝕧[/math]	(generic temperament multivector)					[math]\scriptsize (1, {{d}\choose{r}})[/math] or [math]\scriptsize (1, {{d}\choose{n}})[/math]	integer	multivector	⟨...] or ⟨⟨...]] or ⟨⟨⟨...]]] ...	[...⟩ or [[...⟩⟩ or [[[...⟩⟩⟩ ...				[math]𝕧_i[/math]
	[math]A[/math]	(generic temperament matrix)					[math]\scriptsize (g, d)[/math] or [math]\scriptsize (d, g)[/math]	integer	matrix	[⟨...] ...}	⟨[...} ...] or [[...⟩ ...]	[math]𝒂_i[/math]	[math]𝒂_i[/math]	[math]𝒂[/math]	[math]a_{ij}[/math]
	[math]v[/math]	variance
	[math]g[/math]	grade					[math]\scriptsize (1, 1)[/math]	integer	scalar
temperament addition
[math]\min(r, n)[/math]	[math]g_\text{min}[/math]	min-grade					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]\max(r, n)[/math]	[math]g_\text{max}[/math]	max-grade					[math]\scriptsize (1, 1)[/math]	integer	scalar
	[math]L_\text{dep}[/math]	linear-dependence basis					[math]\scriptsize (l_\text{dep}, d)[/math] or [math]\scriptsize (d, l_\text{dep})[/math]	integer	matrix	[⟨...]] or [[...] ...⟩	⟨[...]] or [[...⟩ ...]	[math]{\large\textbf{𝓁}}\hspace{2mu}_{\text{dep}i}[/math]	[math]{\large\textbf{𝓁}}\hspace{2mu}_{\text{dep}i}[/math]	[math]{\large\textbf{𝓁}}\hspace{2mu}_\text{dep}[/math]	[math]{\large 𝓁}\hspace{2mu}_{\text{dep}ij}[/math]
	[math]L_\text{ind}[/math]	linear-independence basis					[math]\scriptsize (l_\text{ind}, d)[/math] or [math]\scriptsize (d, l_\text{ind})[/math]	integer	matrix	[⟨...]] or [[...] ...⟩	⟨[...]] or [[...⟩ ...]	[math]{\large\textbf{𝓁}}\hspace{2mu}_{\text{ind}i}[/math]	[math]{\large\textbf{𝓁}}\hspace{2mu}_{\text{ind}i}[/math]	[math]{\large\textbf{𝓁}}\hspace{2mu}_\text{ind}[/math]	[math]{\large 𝓁}\hspace{2mu}_{\text{ind}ij}[/math]
[math]\dim(L_\text{dep})[/math]	[math]l_\text{dep}[/math]	linear-dependence					[math]\scriptsize (1, 1)[/math]	integer	scalar
[math]\dim(L_\text{ind})[/math]	[math]l_\text{ind}[/math]	linear-independence					[math]\scriptsize (1, 1)[/math]	integer	scalar

Units


symbol	name	vectorized
[math]\small 𝗴[/math]	generators	yes
[math]\small 𝗽[/math]	primes	yes
[math]\small 𝗯[/math]	(subspace) basis elements	yes
[math]\small 𝗕[/math]	superspace basis elements	yes
[math]\mathsf{¢}[/math]	cents
[math]\mathsf{¢}\small{(}[/math]<weight>[math]\small\mathsf{)}[/math]	weighted cents
[math]\small\mathsf{oct}[/math]	octaves

Tuning schemes


retuning (or mistuning) magnitude						damage												target intervals	systematic name		previously named tuning schemes that are specific types of this tuning scheme	of interest?
						weight									optimization
						interval complexity						slope			initial	name	power
norm pretransformer			norm power			norm pretransformer			norm power			initial	name	multiplier
initial	name	multiplier	initial	name	power	initial	name	multiplier	initial	name	power	initial	name	multiplier					abbreviated	read ("____ tuning scheme")
<none>			<n/a>	maximum	∞	<none>			(t)	taxicab	1	S	simplicity-weight	1/complexity	<n/a>	minimax	∞	all	minimax-S	minimax simplicity-weight damage	"TOP"/"T1"/"TIPTOP", "CTOP", "POTOP"/"POTT"	yes
<various>				maximum	∞	<various>			(t)	taxicab	1								minimax-<alt>-S	minimax <alternative>-simplicity-weight damage	"BOP", "Weil", "Kees"	yes
<none>				Euclidean	2	<none>			E	Euclidean	2								minimax-ES	minimax Euclideanized-simplicity-weight damage	"TE"/"T2"/"TOP-RMS", "CTE", "POTE"	yes
<various>				Euclidean	2	<various>			E	Euclidean	2								minimax-E-<alt>-S	minimax Euclideanized-<alternative>-simplicity-weight damage	"Frobenius", "BE", "WE", "KE"	yes
<n/a>						<n/a>						U	unity-weight	<none>				<set>	<set> minimax-U	<set> minimax unity-weight damage	"minimax"	yes
						<none>			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> minimax-S	<set> minimax simplicity-weight damage		yes
						<various>			(t)	taxicab	1								<set> minimax-<alt>-S	<set> minimax <alternative>-simplicity-weight damage
						<none>			E	Euclidean	2								<set> minimax-ES	<set> minimax Euclideanized-simplicity-weight damage
						<various>			E	Euclidean	2								<set> minimax-E-<alt>-S	<set> minimax Euclideanized-<alternative>-simplicity-weight damage
						<none>			(t)	taxicab	1	C	complexity-weight	complexity					<set> minimax-C	<set> minimax complexity-weight damage		yes
						<various>			(t)	taxicab	1								<set> minimax-<alt>-C	<set> minimax <alternative>-complexity-weight damage
						<none>			E	Euclidean	2								<set> minimax-EC	<set> minimax Euclideanized-complexity-weight damage
						<various>			E	Euclidean	2								<set> minimax-E-<alt>-C	<set> minimax Euclideanized-<alternative>-complexity-weight damage
						<n/a>						U	unity-weight	<none>		miniRMS	2		<set> miniRMS-U	<set> miniRMS unity-weight damage	"least squares"	yes
						<none>			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> miniRMS-S	<set> miniRMS simplicity-weight damage		yes
						<various>			(t)	taxicab	1								<set> miniRMS-<alt>-S	<set> miniRMS <alternative>-simplicity-weight damage
						<none>			E	Euclidean	2								<set> miniRMS-ES	<set> miniRMS Euclideanized-simplicity-weight damage
						<various>			E	Euclidean	2								<set> miniRMS-E-<alt>-S	<set> miniRMS Euclideanized-<alternative>-simplicity-weight damage
						<none>			(t)	taxicab	1	C	complexity-weight	complexity					<set> miniRMS-C	<set> miniRMS complexity-weight damage		yes
						<various>			(t)	taxicab	1								<set> miniRMS-<alt>-C	<set> miniRMS <alternative>-complexity-weight damage
						<none>			E	Euclidean	2								<set> miniRMS-EC	<set> miniRMS Euclideanized-complexity-weight damage
						<various>			E	Euclidean	2								<set> miniRMS-E-<alt>-C	<set> miniRMS Euclideanized-<alternative>-complexity-weight damage
						<n/a>						U	unity-weight	<none>		miniaverage	1		<set> miniaverage-U	<set> miniaverage unity-weight damage		yes
						<none>			(t)	taxicab	1	S	simplicity-weight	1/complexity					<set> miniaverage-S	<set> miniaverage simplicity-weight damage		yes
						<various>			(t)	taxicab	1								<set> miniaverage-<alt>-S	<set> miniaverage <alternative>-simplicity-weight damage
						<none>			E	Euclidean	2								<set> miniaverage-ES	<set> miniaverage Euclideanized-simplicity-weight damage
						<various>			E	Euclidean	2								<set> miniaverage-E-<alt>-S	<set> miniaverage Euclideanized-<alternative>-simplicity-weight damage
						<none>			(t)	taxicab	1	C	complexity-weight	complexity					<set> miniaverage-C	<set> miniaverage complexity-weight damage		yes
						<various>			(t)	taxicab	1								<set> miniaverage-<alt>-C	<set> miniaverage <alternative>-complexity-weight damage
						<none>			E	Euclidean	2								<set> miniaverage-EC	<set> miniaverage Euclideanized-complexity-weight damage
						<various>			E	Euclidean	2								<set> miniaverage-E-<alt>-C	<set> miniaverage Euclideanized-<alternative>-complexity-weight damage

Damages


quantity		unit
abbreviation	name	symbol	name
U-damage	unity-weight damage	[math]\mathsf{¢}\small\mathsf{(U)}[/math]	unity-weighted cents
C-damage	complexity-weight damage	[math]\mathsf{¢}\small\mathsf{(C)}[/math]	complexity-weighted cents
<alt>-C-damage	<alternative>-complexity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{C)}[/math]	<alternative>-complexity-weighted cents
EC-damage	Euclideanized-complexity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(EC)}[/math]	Euclideanized-complexity-weighted cents
E-<alt>-C-damage	Euclideanized-<alternative>-complexity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(E}[/math]-<alt>-[math]\small\mathsf{C)}[/math]	Euclideanized-<alternative>-complexity-weighted cents
S-damage	simplicity-weight damage	[math]\mathsf{¢}\small\mathsf{(S)}[/math]	simplicity-weighted cents
<alt>-S-damage	<alternative>-simplicity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{S)}[/math]	<alternative>-simplicity-weighted cents
ES-damage	Euclideanized-simplicity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(ES)}[/math]	Euclideanized-simplicity-weighted cents
E-<alt>-S-damage	Euclideanized-<alternative>-simplicity-weight damage	[math]\mathsf{¢}[/math][math]\small\mathsf{(E}[/math]-<alt>-[math]\small\mathsf{S)}[/math]	Euclideanized-<alternative>-simplicity-weighted cents

Complexity and simplicity


quantity		unit
abbreviation	name	unit	name
C	complexity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(C)}[/math] = [math]\small\mathsf{(C)}[/math]	complexity weight
<alt>-C	<alternative> complexity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(}[/math]<alt>-[math]\scriptsize\mathsf{C)}[/math] = [math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{C)}[/math]	<alternative>-complexity weight
EC	Euclideanized complexity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(EC)}[/math] = [math]\small\mathsf{(EC)}[/math]	Euclideanized-complexity weight
E-<alt>-C	Euclideanized-<alternative> complexity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(E}[/math]-<alt>-[math]\scriptsize\mathsf{C)}[/math] = [math]\small\mathsf{(E}[/math]-<alt>-[math]\small\mathsf{C)}[/math]	Euclideanized-<alternative>-complexity weight
S	simplicity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(S)}[/math] = [math]\small\mathsf{(S)}[/math]	simplicity weight
<alt>-S	<alternative> simplicity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(}[/math]<alt>-[math]\scriptsize\mathsf{S)}[/math] = [math]\small\mathsf{(}[/math]<alt>-[math]\small\mathsf{S)}[/math]	<alternative>-simplicity weight
ES	Euclideanized simplicity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(ES)}[/math] = [math]\small\mathsf{(ES)}[/math]	Euclideanized-simplicity weight
E-<alt>-S	Euclideanized-<alternative> simplicity	[math]\small\mathsf{𝟙}\scriptsize\mathsf{(E}[/math]-<alt>-[math]\scriptsize\mathsf{S)}[/math] = [math]\small\mathsf{(E}[/math]-<alt>-[math]\small\mathsf{S)}[/math]	Euclideanized-<alternative>-simplicity weight

WinCompose

Are you tired of every time web-searching for and copy-pasting special characters that you use over and over in RTT discussions, or would like to use if only it were easy, such as ♯, ♭, ¢, √, °, ₂, ×, ⁻¹, ⟩, ∞, and ϕ? Well, try WinCompose! This tool lets you communicate about these ideas without disrupting your train of thought, by typing these characters with simple and memorable key sequences. These sequences always begin with your chosen Compose-key, which defaults to being your right Alt key. When describing these sequences we represent this key with the symbol ⎄. So for example, you type ♯ as ⎄##, ♭ as ⎄bb, ¢ as ⎄c/, √ as ⎄v/, ° as ⎄00, ₂ as ⎄-2, × as ⎄xx, ⁻¹ as ⎄11, ⟩ as ⎄>>, ∞ as ⎄88, and ϕ as ⎄8f.

For Windows users, install WinCompose then copy-paste the contents of this file: https://dkeenan.com/XCompose.txt into your user sequences (Show sequences → User-defined sequences → Edit). Then save and reload. You can always choose to override or add alternatives to our sequences if you find others to be more intuitive.

For Mac users, we refer you to this repo, which gives tools and instructions for setting up key bindings as compose rules in Mac OS, and even comes pre-packaged with our rules: https://github.com/cmloegcmluin/compose2keybindings

Table of noteworthy sequences


Compose-key sequence	resulting text	description
Keyboard key symbols
⎄⎄⎄	⎄	compose key symbol (the right alt key by default)
⎄\␣	␣	spacebar symbol
⎄\▶︎ etc.	▶︎ etc.	right etc. arrow key symbols
⎄\A or ⎄\O	⌥	alt or option key symbol
⎄\B	⌫	backspace key symbol
⎄\C	✲	control key symbol
⎄\D	⌦	delete key symbol
⎄\E	⎋	escape key symbol
⎄\L	⇪	caps lock key symbol
⎄\R or ⎄\.E	⏎	return or enter key symbol
⎄\S	⇧	shift key symbol
⎄\T	⭾	tab key symbol
⎄()	◌	dotted circle, represents any character (such as the character preceding a combining mark)
Double key sequences
⎄␣␣		narrow no-break space (used between quantities and their units)
⎄..	·	middle dot (used to multiply units when juxtaposition is ambiguous)
⎄::	÷	divide sign
⎄;;	◌̲̅	combining overline and low line (undirected value)
⎄\|\|	‖	power norm bracket
⎄<<	⟨	left angle bracket
⎄>>	⟩	right angle bracket
⎄~~	≈	approximately equal
⎄**	★	black star
⎄''	′	prime mark
⎄11	⁻¹	power of -1 or inverse
⎄22 through ⎄77	² ³ ⁴ ⁵ ⁶ ⁷	squared, cubed, fourth through seventh power
⎄88	∞	infinity
⎄00	°	degree sign
⎄nn	ⁿ	superscript small n
⎄--	₋	subscript minus sign
⎄__	◌̲	combining low line (underline)
⎄==	≡	modular congruence
⎄//	⁄	fraction slash (use with super and subscripts to create fractions)
⎄##	♯	musical sharp
⎄bb	♭	musical flat
⎄dd	∂	partial derivative
⎄ff	ϕ	small phi symbol
⎄gg	ɡ	single-storey (opentail) small g
⎄ll	ℓ	script small L
⎄uu	µ	micro sign
⎄xx	×	multiplication sign
⎄DD	∆	delta (small difference) operator
⎄FF	Φ	Greek capital phi
⎄QQ	Ϙ	Greek capital letter archaic qoppa (small quotient operator)
⎄TT	ᵀ	superscript capital T (matrix transpose)
⎄++	⁺	superscript plus sign (matrix pseudoinverse)
⎄▶︎▶︎ etc.	→ etc.	right etc. arrows
Multiplication operators
⎄xx	×	multiplication sign
⎄Xx or ⎄xX	⨯	vector or cross product (barely distinguishable from multiplication sign)
⎄XX	✕	large multiplication sign (a better symbol for cross product)
⎄x*	⋆	star operator (prefix: tensor complement, Hodge)
⎄X*	∗	asterisk operator (infix: scalar product, Dorst)
⎄x.	⋅	dot (product) operator
⎄X.	•	bullet (infix: fat dot product, Dorst)
Other operators
⎄v/	√	square root sign
⎄3v/	∛	cube root sign
⎄4v/	∜	fourth root sign
⎄-+	₊	subscript plus sign
⎄--	₋	subscript minus sign
⎄-=	₌	subscript equals sign
⎄++	⁺	superscript plus sign (matrix pseudoinverse)
⎄+- or ⎄+=	±	plus or minus sign
⎄=+	∓	minus or plus sign
⎄=-	−	minus sign
⎄==	≡	modular congruence
⎄/\	∧	logical AND, wedge product, progressive product
⎄\/	∨	logical OR, vee product, regressive product
⎄⎄/\	⋀	larger logical AND, wedge product, progressive product
⎄⎄\/	⋁	larger logical OR, vee product, regressive product
⎄\|_	⌊	left floor (infix: right contraction, Dorst)
⎄_\|	⌋	right floor (infix: left contraction, Dorst)
⎄\|^	⌈	left ceiling
⎄^\|	⌉	right ceiling
⎄'-	⨽	righthand interior product
⎄-'	⨼	(lefthand) interior product
⎄-,	¬	not sign (prefix: multivector complement)
⎄⎄<>	⋄	diamond operator (prefix: multivector dual)
⎄(.)	⨀	entrywise vector multiplication operator
⎄(..)	⊙	alternative entrywise vector multiplication operator
⎄(/)	⊘	entrywise vector division operator
Mathematical letter and digit prefixes
⎄3◌	я	cyrillic, ⎄3q is ya (example)
⎄4◌	ℵ	hebrew, ⎄4a is aleph (example)
⎄5◌	𝔞	fraktur, ⎄5a
⎄6◌	ᵃ ¹  ᪲ ⁸	superscripts, ⎄6a ⎄61 ⎄688 ⎄68␣ (not all letters, some only approximate) (same key as ^ but without shift)
⎄68◌	ᵝ	superscript greek, ⎄68b is superscript beta (only a few)
⎄7◌	𝒶	script, ⎄7a
⎄8◌	α	greek, ⎄8a is alpha (by sound where possible otherwise letter-shape)
⎄8.◌	ς	greek variants, ⎄8.s is final sigma
⎄9◌	𝐚 𝟏 𝟓 𝟕 𝟖 𝟎	bold, ⎄9a ⎄91 ⎄95␣ ⎄97␣ ⎄98␣ ⎄90␣
⎄95◌	𝖆	bold fraktur, ⎄95a
⎄97◌	𝓪	bold script, ⎄97a
⎄98◌	𝛂	bold greek, ⎄98a is bold alpha
⎄90◌	𝒂	bold italic, ⎄90a
⎄908◌	𝜶	bold italic greek, ⎄908a is bold italic alpha
⎄0◌	𝑎	italic, ⎄0a
⎄08◌	𝛼	italic greek, ⎄08a is italic alpha
⎄-◌	ₐ ᴀ  ͚ ₈	subscripts and small caps, ⎄-a ⎄-A ⎄-88 ⎄-8␣ (not all letters, some only approximate) (same key as _ but without shift)
⎄-8◌	ᵦ	subscript greek, ⎄-8b is subscript beta (only a few)
⎄{◌	𝖺 𝟣 𝟫	sans-serif, ⎄{a ⎄{1 ⎄{9␣
⎄{9◌	𝗮 𝟭	sans-serif bold, ⎄{9a ⎄{91
⎄}◌	𝚊 𝟷	monospace, ⎄}a ⎄}1
⎄\|◌	𝕒 𝟙 𝟠 𝟘	double-struck, ⎄\|a ⎄\|1 ⎄\|8␣ ⎄\|0␣
⎄\|8◌	ℼ	double-struck greek, ⎄\|8p (only a few)
⎄\|0◌	ⅇ ⅈ	double-struck italic, ⎄\|0e ⎄\|i (only a few)
Power statistics brackets
⎄\|\|	‖	power-norm bracket
⎄\|-1	‖₁	1-norm right bracket
⎄\|-2	‖₂	2-norm right bracket
⎄\|-8	‖ ͚	∞-norm right bracket
⎄⎄<<	⟪	left power-mean bracket
⎄⎄>>	⟫	right power-mean bracket
⎄⎄{{	⧛	left power-sum bracket (substitute for ꗨꗨ when HTML is not available)
⎄⎄}}	⧚	right power-sum bracket (substitute for ꗨꗨ when HTML is not available)
Combining marks
⎄\-	◌̶	combining strike-thru
⎄^_	◌̅	combining overline
⎄__	◌̲	combining low line
⎄;; or ⎄-_ or ⎄_^	◌̲̅	combining overline and low line (undirected value)

Keyboard map

Footnotes

↑ The advanced section also contains conventions collected from other RTT-related articles Dave and Douglas have contributed to but are outside the main guide to RTT series.
↑ For educational purposes, we use the 𝟙 symbol here to represent the implicit dimensionless unit that the weighting annotation "(C)" is attached to. But this symbol should not be shown in the reduced result. Another way to understand how we arrive at a bare annotation for the units of this quantity is to consider that w = d / |e| whose units are ¢(W) / ¢ and the cents cancel.
↑ You may sometimes see annotated units without parentheses, such as "dBA", but this is not compliant with SI standards, so we always keep the parentheses.
↑ Per https://physics.nist.gov/cuu/Units/checklist.html and https://academia.stackexchange.com/questions/54885/should-there-be-a-space-between-a-value-and-the-units-used .
↑ It seems there is no standard symbol for a musical cent, except the word spelled in full (see https://en.wikipedia.org/wiki/Cent_(music)). But it seems unlikely anyone will interpret the cent currency symbol "¢" following a number in a musical context as anything other than musical cents.
↑ In these tables, "alternative" means any complexity other than the default of log-product complexity, and "alt" stands for its abbreviation.
↑ May be used for a prime-limit or for any prime-only list.

[1] The advanced section also contains conventions collected from other RTT-related articles Dave and Douglas have contributed to but are outside the main guide to RTT series.

[2] For educational purposes, we use the 𝟙 symbol here to represent the implicit dimensionless unit that the weighting annotation "(C)" is attached to. But this symbol should not be shown in the reduced result. Another way to understand how we arrive at a bare annotation for the units of this quantity is to consider that w = d / |e| whose units are ¢(W) / ¢ and the cents cancel.

[3] You may sometimes see annotated units without parentheses, such as "dBA", but this is not compliant with SI standards, so we always keep the parentheses.

[4] Per https://physics.nist.gov/cuu/Units/checklist.html and https://academia.stackexchange.com/questions/54885/should-there-be-a-space-between-a-value-and-the-units-used .

[5] It seems there is no standard symbol for a musical cent, except the word spelled in full (see https://en.wikipedia.org/wiki/Cent_(music)). But it seems unlikely anyone will interpret the cent currency symbol "¢" following a number in a musical context as anything other than musical cents.

[6] In these tables, "alternative" means any complexity other than the default of log-product complexity, and "alt" stands for its abbreviation.

[7] May be used for a prime-limit or for any prime-only list.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Dave Keenan & Douglas Blumeyer's guide to RTT: conventions for names, variables, units, and notations

Contents

Basic

Objects

Units

Tuning schemes

Damages

Complexity and simplicity

Intermediate

Objects

Units

Tuning schemes

Damages

Complexity and simplicity

Advanced

Objects

Units

Tuning schemes

Damages

Complexity and simplicity

WinCompose

Table of noteworthy sequences

Keyboard map

Footnotes

Navigation menu

Search