AID
Arithmetic irrational divisions
For an intervallic system with n divisions, AID is considered as arithmetic sequence with divisions of system as terms of sequence.
If the first division is A1 and the last, An , with common difference of d , we have :
- A1 = A1
- A2 = A1+d
- A3 = A1+2d
- A4 = A1+3d
- ...
- An = A1+(n-1)d
So sum of the divisions is Sn :
- Sn =( n[2A1+(n-1)d])/2
As we can consider Sn of system to be 1200 cent or anything else (octavic or non-octavic system ) then d is most important to make an AID with n divisions with A1. So, the common difference between divisions is :
- d =( 2(Sn - nA1))/(n(n-1))
By considering Sn=1200, A1=70, n=12, d will be 5.454545455 and our 12-tone scale is equal to:
- 0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0
Scales based on AID can be subsets of EDO if:
- we choose d=0 so, A1 = Sn/n .. Consider n=8 and A1=150, then we have 8-EDO .
- for a constant n and different A1, if d and (Sn/A1) are integers, we have a subset of EDO or EDI (Equal divisions of Interval).
Consider Sn = 1400 , n=8 and A1=70, then we have a subset of a 140-ED (1400.) with Degrees as 7 17 30 46 65 87 112 140 :
- 0.0 70.0 170.0 300.0 460.0 650.0 870.0 1120.0 1400.0
And now for Sn=1400 and n=8,
- If A1=175.0 then we have 8-AID(1400.)
- If A1=56 then we have 700-AID(1400.) with Degrees as 28 73 135 214 310 423 553 700
- If A1=87.5 then we have 112-AID(1400.) with Degrees as 7 16 27 40 55 72 91 112
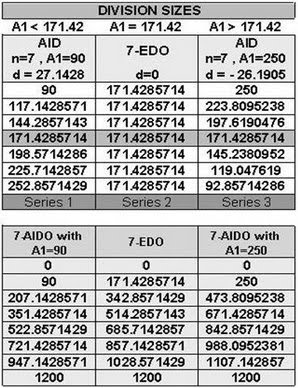
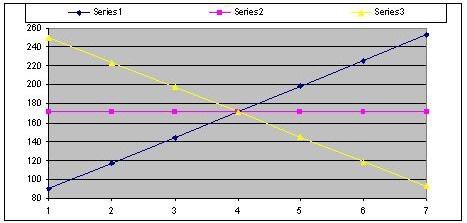
AID system shows different ascending, descending or linear trend of change in divisions sizes due to relation between n and A1 in AID and EDO with equal degree:
- If choosing A1 greater than division size in equal degree EDO, d is negative and AID is descending.
- If choosing A1 smaller than division size in equal degree EDO, d is positive and AID is ascending.
- If choosing A1 equal to division size in equal degree EDO, d is zero.
171.4285714 is point of intersection in these 3 trends:
We can have different kinds of AID:
- AIDO = Arithmetic irrational divisions of octave
- AIDINO = Arithmetic irrational divisions of irrational non-octave
- AIDRNO = Arithmetic irrational divisions of rational non-octave
- AIDRI = Arithmetic irrational divisions of rational interval
- AIDII = Arithmetic irrational divisions of irrational interval
Example: Baran scale