Defactoring

Defactoring is a operation on the mapping for a regular temperament which ensures it represents the same information but without any enfactoring, or in other words, redundancies due to a common factor found in its rows. It is also defined for comma bases, the duals of mappings, where it instead checks its columns for enfactoring.

Being enfactored is a bad thing. Enfactored matrices — those in the RTT domain, at least — are sick, in a way; it's no accident that "enfactored" sounds sort of like "infected". We'll discuss this pathology in detail in a later section of this article. Fortunately, the remedy is simple: all one has to do is "defactor" it — identify and divide out the common factor — to produce a healthy mapping.

Due to complications associated with enfactored matrices which we'll get into later in this article, we discourage treating them as representations of true temperaments. Instead we recommend that they be considered to represent mere "temperoids": temperament-like structures.

More specific definition

A mapping is enfactored if linear combinations of its rows can produce another row whose elements have a common factor (other than 1).

For example, [⟨3 0 -1] ⟨0 3 5]⟩ is enfactored, because ⟨3 0 -1] - ⟨0 3 5] = ⟨3 -3 -6], which has a common factor of 3.

This definition includes mappings whose rows themselves include a common factor, such as [⟨24 38 56]⟩, which already has a clearly visible common factor of 2.

Motivation

A major use case for defactoring is to enable a canonical form for temperament mappings, or in other words, to achieve for the linear-algebra-only school of RTT practitioners a unique ID for temperaments. Previously this was only available by using lists of minor determinants AKA wedge products of mapping rows, which by virtue of reducing the information down to a single list of numbers, could be checked for enfactoring by simply checking the single row's GCD. For more information on this historical situation, see: Varianced Exterior Algebra#Lack of importance to RTT, and for more information on the canonical form developed, see defactored Hermite form.

Terminology change proposal

If you've studied RTT extensively, you've probably encountered the terms "saturated" and "contorted" that are sometimes used to describe mappings. These two terms each have several flaws, and so this article presents alternative terms that are clearer and more descriptive: "defactored" and "enfactored", respectively. These new terms were coined by Dave Keenan in collaboration with Douglas Blumeyer in June of 2021.

Defactored, to replace saturated

Several concerns with the term "saturation" may be identified:

1. It does not have any obvious musical or mathematical meaning in this context (whereas enfactored and defactored do have obvious mathematical meaning).
2. It has another unrelated meaning within xenharmonics that it would conflict with: https://en.xen.wiki/w/Anomalous_saturated_suspension
3. The most common everyday usage of that word is for "saturated fats", which are the bad kind of fats, so it has negative associations, despite "saturation" being the good state for a matrix to be in.
4. Research on the tuning list archives suggests that Gene Ward Smith chose the word "saturation" because it was used in the mathematical software he was using at the time, Sage. However, no information about saturation indices has been identified elsewhere online. Certainly, if this mathematical concept of saturation is established outside of this particular piece of software, it is not well-established enough yet such that it's worth deferring to. We think we should avoid propagating Sage's decision to overload matrix saturation with a second meaning.
5. Furthermore, there is another common but conflicting sense of saturation for matrices which clamps entry values to between -1 and 1.

Enfactored, to replace contorted

As for the term "contorsion", the concerns with it are:

1. Again, it does not have any obvious musical or mathematical meaning in this context. It's a word that was invented for RTT, so nothing else depends on it.
2. It was made up due to false assumptions. Through researching on tuning list archives, Dave and Douglas concluded that the associated concept of "torsion" was first described in January of 2002, with regards to commas used to form Fokker periodicity blocks. The concept of enfactoring was recognized in temperament mappings (though of course it did not yet go by that name), and — because torsion in lists of commas for Fokker blocks looks the same way as enfactoring looks in temperament comma bases — torsion got conflated with it. But they can't truly be the same thing; the critical difference is that periodicity blocks do not involve tempering, while temperaments do. In concrete terms, while it can make sense to construct a Fokker block with [-4 4 -1⟩ in the middle and [-8 8 -2⟩ = 2[-4 4 -1⟩ at the edge, it does not make sense to imagine a temperament which tempers out 2[-4 4 -1⟩ but does not temper out [-4 4 -1⟩. Unfortunately, however, this critical difference seems to have been overlooked, and so it seemed that enfactored comma bases exhibited torsion, and thus because mappings are the dual of comma bases, then enfactoring of a mapping should be the dual of torsion, and because the prefix co- or con- means "dual" (as in vectors and covectors), the term "con-torsion" was coined for it. "Torsion" already has the problem of being an obscure mathematical term that means nothing to most people, "contorsion" just compounds that problem by being made up, and it is made up in order to convey a duality which is false. So while "torsion" could be preserved as a term for the effect on periodicity blocks (though there's almost certainly something more helpful than that, but that's a battle for another day), they feel it would be better to banish the term "contorsion" from the RTT community altogether.
3. A word with the same spelling was also coined with a different mathematical meaning outside of RTT, in the field of differential geometry: https://en.wikipedia.org/wiki/Contorsion_tensor
4. It is prone to spelling confusion. People commonly refer to temperaments with contorsion as "contorted". But contorted is the adjective form of a different word, contortion, with a t, not an s. The proper adjective form of contorsion would be contorsioned. Would you use "torted" instead of torsioned? Or would people prefer "torsional" and "contorsional", even though that suggests only of or pertaining to in general rather than having the effect applied.
5. Due to its similarity with the word "contortion", the word contorsion evokes bending, twisting, and knotting. But there is nothing bendy, twisty, or knotted about the effect it has on JI lattices or tuning space.

Conclusion

In accordance with this research and reasoning, this article henceforth will eschew the terms saturation and contorsion in favor of defactored and enfactored.

The pathology of enfactoredness

In this section, we will use lattices to visualize enfactored temperaments, to demonstrate the musical implications of mappings with common factors, and the lack of musical implications of comma bases with common factors.

Defactored case

A 3-limit tempered lattice, superimposed on the JI lattice

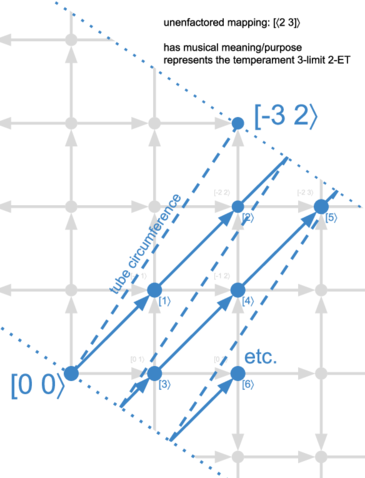
First, let's look at an defactored mapping. This example temperament is so simple that it is not of practical musical interest. It was chosen because it's basically the numerically simplest possible example, where this type of simplicity empowers us to visualize the problem at a practical scale as clearly as possible. Please consider the diagram at right.

This is a representation of 2-ET, a 3-limit, rank-1 (equal) temperament, with mapping [⟨2 3]⟩, meaning it has a single generator which takes two steps to reach the octave, and three steps to reach the tritave. This temperament tempers out a single comma, whose vector representation looks similar to the mapping: [-3 2⟩, AKA 9/8. And so the comma basis for this temperament is ⟨[-3 2⟩].

We can imagine that we started out with a JI lattice, where movement up and down correspond to prime 2 (the octave) and movements right and left correspond to prime 3 (the tritave). We have tempered JI here, and so we've faded the JI lattice out to a faint grey color in the background. What we've done specifically is tempered out the comma [-3 2⟩ so that any nodes in this lattice which are 2 over and 3 up from each other are equivalent. Therefore we only need to consider a thin swath of the lattice anymore, specifically, a swath which connects the origin [0 0⟩, AKA 1/1, to [-3 2⟩, and then runs perpendicularly to infinity in either direction.

There's a couple good ways to interpret this situation:

1. We've turned on a teleportation field for every point outside this swath, so that it moves by these (-3,2) intervals until it finds its way inside the swath.
2. We've rolled up space, so that the line from 1/1 to 9/8 ₋ the width of our swath ₋ is like the circumference of a tube. In this case, since we're only working with 3-limit JI, "space" was only ever 2D, so we can just think of it as paper that we've rolled up, so the pair of dotted lines visualized here are touching along their entire lengths (and if you wanted to imagine further copies of these dotted lines at every (-3,2) interval farther out in either direction, and the paper is infinitely thin, just stack all the dotted lines on top of each other forever).

Either way, then we just superimpose the new tempered lattice on top. It's drawn in blue.

You can see that in the grey lattice underneath, coordinates have 2 values, e.g. [-1 2⟩. That's because the JI lattice essentially had two generators: the octave and the tritave. But tempering has helped us simplify things by reducing us to a single generator, so here, in the new blue-colored tempered lattice, the coordinates have only 1 value, e.g. [8⟩, and they simply indicate how many iterations of the single generator here that we've taken to reach the given point.

We've superimposed the tempered lattice atop the former JI lattice so we can see which JI intervals map to which tempered intervals. For example, [-1 2⟩, AKA 9/2, maps to [8⟩. That tells us that if we want to use the temperament's approximation of the JI interval 9/2, then we want the tempered pitch arrived at by moving by the generator 8 times.

Note that whenever the path the generator takes leaves the main swath, it wraps around to the point on the opposite side. Again, you can think of this either way you prefer: the world is still flat, and you've just warped over there; or, the world has been curled up, and in reality you've been looping back around toward that point the whole time, and the dotted line in this flat representation just represents the point you cut the tube and unrolled it so it could be better visualized on a screen.

The tempered vector for the generator of this temperament is of course [1⟩, but the JI preimage of the generator of this temperament is [-1 1⟩, or 3/2. It's visually clear why this is the generator. We need to choose an interval which if we repeatedly move by it, while wrapping around the swath, we'll visit every node inside the swath. The best way to do that is to move from the origin to the node that's nearest to the dotted line labelled "tube circumference". We want this node because we want to move away from the tube circumference as little as possible each time, so we avoid skipping any nodes. If it's not obvious, you may want to experiment with drawing the generator line as if it had gone to any other point inside the swath; if you repeated that movement, would you visit every node? No.

All of this so far is actually only just explaining the basic setup for any tempered lattice. But we've got to lay the basics down first in order to discuss the effect of enfactoring. We'll do that now!

Enfactored mapping

A 2-enfactored mapping represents a temperoid for which every other step of its generator lands on a pitch which no JI interval would ever temper to.

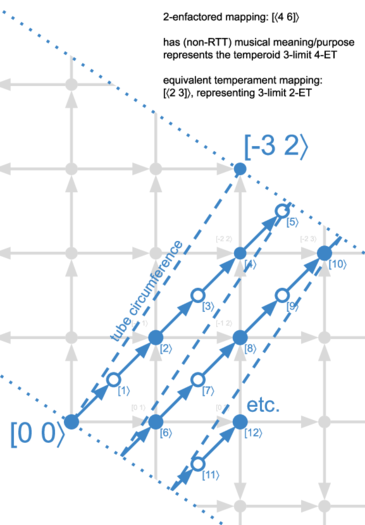
We are now comparing the previous diagram, which had the mapping [⟨2 3]⟩, with the 2-enfactored version of it, i.e. the mapping 2×[⟨2 3]⟩ = [⟨4 6]⟩, AKA 4-ET.

If you compare this lattice of an enfactored mapping with the previous lattice for a healthy, defactored mapping, they should look almost the same. They have the same comma and tube circumference. And the generator follows the same path through that tube/swath. The key difference is how far the generator moves with each step along that path.

Starting from the origin, we can see that it takes us 2 moves of the generator to reach the approximation of [-1 1⟩, AKA 3/2, where before we made that step in one go. Then another 2 moves to reach the approximation of [-2 2⟩, AKA 9/4, for a total of 4 moves, where before it only took us 2 steps. As you keep going, you'll see that each node it has taken us 2x as many steps as before to reach it.

And for what? What happens in the steps that are halfway between nodes that were on the JI lattice? These are shown with hollow blue circles instead of filled blue circles, to indicate that there's not JI lattice node underneath them. In other words, while these are legitimate musical intervals, there is no JI interval which would be said to temper to them. In other words, since this is 4-ET, that first generator step is to a node [1⟩ that's about 300¢. But [0 0⟩ tempers to [0⟩ and [-1 1⟩ tempers to [2⟩; nothing tempers to [1⟩. It's an interval that can certainly at least be heard and understood musically, but has no meaning with respect to tempering JI, or in other words, no RTT purpose.

And so this 4-ET doesn't bring anything to the table that isn't already brought by 2-ET. And so it is fitting to consider it only a temperoid, rather than a true temperament. Were this as bad as things got, it might not be worth pushing for distinguishing temperoids from temperaments. But once we look at enfactored comma bases, we'll see why things get pretty pathological.

Enfactored comma bases

File:2-enfactored comma basis.png

enfactored comma bases are garbage

Here's where things get kind of nuts. Most recently we experimented with enfactoring our healthy temperament's mapping. Now let's experiment with enfactoring its comma basis. In the defactored situation, if our comma basis was ⟨[-3 2⟩], then 2-enfactoring it produces 2×⟨[-3 2⟩] = ⟨[-6 4⟩].

We know that in the original diagram, the large-labelled [-3 2⟩ represented our comma, and this was the point that our dotted line ran through, the one that represented our boundary of warp/wrap. So our first thought should be: we must alter our diagram so that now [-6 4⟩ is that point instead. Fine.

But here's the problem. It simply doesn't make sense to double the width of our swath/tube! If [-6 4⟩ is tempered out, then so is [-3 2⟩. That is, while nothing would stop you from drawing a diagram with a double-width swath/tube, the musical reality is that it is impossible to temper out [-6 4⟩ without also tempering out [-3 2⟩. And so there is no meaning or purpose to the comma basis [-6 4⟩, whether RTT-wise or musically in general. It is garbage.

And so our lattice for an enfactored comma basis looks almost identical to the original defactored lattice. The only difference here is that we've drawn a "supposed (but false)" tube circumference out to [-6 4⟩, while the half of this length which is real is now labelled the "true" circumference.

Enfactored comma bases vs. periodicity blocks with torsion

a reworking of the classic torsion example from Tonalsoft to reveal the twinned generator paths

And now we're prepared to confront the key difference between the enfactored comma basis of a temperament, and torsion of a periodicity block.

What they have in common is that both take the form of a common factor found somewhere in linear combinations of entries in a list of commas defining a pitch structure, and that these commas can be visualized by slicing the JI lattice into swaths of "periodicity" (that's just a fancy word for the effect we've already been observing for temperaments, where nodes outside the swath related by the size of that comma are considered equivalent and therefore redundant, or repetitions of the same pitch class).

The key difference is that the former (temperaments) tempers the commas out, while the latter (periodicity blocks) does not.

Why is this the key difference? Well, remember how in the previous section, the reason we couldn't actually extend the width of the swath/tube to [-6 4⟩ was because the tempering: if [-6 4⟩ is tempered out, then [-3 2⟩ is as well, so the swath/tube cannot legitimately be extended. Since there is no tempering in the case of periodicity blocks, however, the width can legitimately be extended in this way.

Let's take a look at the example given in Tonalsoft's page for torsion. The diagram there has been reworked here to help clarify things. The origin, 1/1, has been placed in the corner of this parallelogram-shaped block, and the two commas that define it are in two of the other corners: 2048/2025 and 625/324. The value at the fourth corner, 12800/6561, has vector 2×[-8 8 -2⟩. The first 2 is just to octave-reduce it to being positive, but you may recognize the actual vector part as 2 times the meantone comma. The most important part is that the vector is 2-enfactored. You can see that the node at the very center of this block is 160/81, which again is 2×[-4 4 -1⟩, or the octave-reduced non-enfactored version of that same comma.

The red and blue lines that wrap around this block are two different generator paths. The point here is to show that by doubling the size of this periodicity block, we have made it impossible to choose a node to travel to from the origin, i.e. a generator, such that you can reach every node in the block. Instead, the best you can do is reach half of the nodes; that's the red path from the origin 1/1. The blue path is an exact copy of the red path, but offset.

So we can see how tempting the duality can be here. In the case of a 2-enfactored mapping, the generator path reaches twice as many nodes as there were JI nodes. But in the case of a 2-enfactored comma basis — if we could legitimately extend the width of the block, as we do in untempered periodicity blocks! — we would reach half as many nodes. But this duality just is not musically, audibly real.

Enfactored mappings vs. enfactored comma bases

One may pose the question: what is the relationship between an enfactored mapping and an enfactored comma basis? Can you have one but not the other? Must you? Or must you not? Or does the question even make sense? Certainly at least some have suggested these cases are meaningfully independent.

The conclusion we arrive at here is that because enfactored comma bases don't make any sense, or at least don't represent any legitimately new musical information of any kind that their defactored version doesn't already represent, it is not generally useful to think of enfactored mappings and enfactored comma bases as independent phenomena. It only makes sense to speak of enfactored temperaments. Of course, one will often use the term "enfactored mapping" because enfactored mappings are the kind which do have some musical purpose, and often the enfactored mapping will be being used to represent the enfactored temperament — or temperoid, that is.

Conclusion

So due to the high likelihood for confusion when conceptualizing enfactored temperaments, we believe that using HNF as the unique ID for temperaments, i.e. treating temperoids as true temperaments, is a dangerous and unhelpful road. Instead, canonical form should be used, essentially HNF but with defactoring built in, so that practitioners of RTT can focus on working with true temperaments.

Identifying enfactored mappings

Immediately apparent enfactoring

Sometimes the enfactoring of a mapping is immediately apparent. For example:

[math]\displaystyle{ \left[ \begin{array} {r} 24 & 38 & 56 \\ \end{array} \right] }[/math]

This mapping has only a single row, and we can see that every element in that row is even. Therefore we have a common factor of at least 2. In this case it is in fact exactly 2. So we can say that this is a 2-enfactored mapping.

Being enfactored tells us that it's wasteful to use this mapping. Specifically, being 2-enfactored tells us that we have 2x as many pitches as we need. Said another way, half of the pitches in our system are bringing nothing to the table, at least not in terms of approximating intervals built out of the 5-limit primes 2, 3, and 5, which is the primary goal of a temperament.

This is the mapping for 5-limit 24-ET. To be clear, we're not saying there's a major problem with 24 as an EDO. The point here is only that — if you're after a 5-limit temperament — you may as well use 12-ET. So we would consider 24-ET to stand for 24 Equal Temperoid.

Think of it this way: because every element is even, any JI interval you'd map with with the mapping must come out as an even number of steps of 24-ET, by the definition of the dot product, and every even step of 24-ET is just a step of 12-ET. Examples: [1 -2 1⟩.⟨24 38 56] = 24 - 76 + 56 = 4, [1 1 -1⟩.⟨24 38 56] = 24 + 38 - 56 = 6.

Hidden enfactoring

Other times, enfactoring is less apparent. Consider this example:

[math]\displaystyle{ \left[ \begin{array} {r} 3 & 0 & -1 \\ 0 & 3 & 5 \\ \end{array} \right] }[/math]

This is a form of 5-limit porcupine, a rank-2 temperament. Looking at either row, neither map has a common factor. But remember that we also need to check linear combinations of rows. If we subtract the 2nd row from the 1st row, we can produce the row ⟨3 -3 -6], which has a common factor of 3. So this mapping is also enfactored, even though it's not obvious from just looking at it.

If you're unsure why this ⟨3 -3 -6] matters despite not being in [⟨3 0 -1] ⟨0 3 5]⟩, we may need to quickly review some linear algebra fundamentals. It may take some getting used to, but a mapping can be changed to another equivalent mapping (both mappings will map input vectors to the same scalars) by replacing any row with linear combinations of its rows. That is, we could replace either ⟨3 0 -1] or ⟨0 3 5] in our original matrix [⟨3 0 -1] ⟨0 3 5]⟩ to get [⟨3 -3 -6] ⟨0 3 5]⟩ or [⟨3 0 -1] ⟨3 -3 -6]⟩ and any of these mappings represent the same temperament.

Well-hidden enfactoring

Sometimes the hidden common factor is even harder to find. Consider the mapping:

[math]\displaystyle{ \left[ \begin{array} {r} 6 & 5 & -4 \\ 4 & -4 & 1 \\ \end{array} \right] }[/math]

To find this common factor, we need to linearly combine two of the first row ⟨6 5 -4] and negative three of the 2nd row ⟨4 -4 1] to produce ⟨0 22 -11]. So we can see here that its common factor is 11. But there's no clear relationship between the numbers 2 and 3 and the number 11. And so we can begin to see that the problem of identifying enfactored mapping may not be very simple or straightforward.

Defactoring methods

Even better than identifying enfactored mappings is actually full-on defactoring them. Here are two methods that do just that: Smith defactoring, developed by Gene Ward Smith, and column Hermite defactoring, developed by Dave and Douglas (the name comes, of course, from Hermite normal form, which it uses).

Neither of these methods have been rigorously proven to always defactor mappings, but tests Douglas ran on thousands of random mappings strongly suggested that both methods work and give the exact same results as each other.

This article prefers column Hermite defactoring to Smith defactoring because it is:

• Cheaper computationally, wasting less resources computing things irrelevant to the result,
• Is easy to understand how it works, and can be worked out by hand (as we will demonstrate below),
• If interested, you can see what the common factor is, if there was any.

Column Hermite defactoring could not have been developed, however, were it not for Gene's pioneering work with the Smith defactoring (what he calls the process of "saturating" a mapping). At first Dave and Douglas had no idea what the right reducing matrix of the Smith decomposition (the process which also provides the Smith normal form) had to do with common factors, only that it somehow magically worked. So they analyzed the Smith decomposition until they isolated its key actions which actually effect the defactoring, and then honed their method down to do only these necessary actions. Again, they wouldn't have known where to start were it not for Gene.

Precedent: Smith defactoring

Dave and Douglas did much of their work in Wolfram Language (formerly Mathematica), a popular programming language used for math problems. In this section we'll give examples using it.

An input mapping [math]\displaystyle{ m }[/math], such as the example Gene gives on the xen wiki page for Saturation, [⟨12 19 28 34] ⟨26 41 60 72]⟩, in Wolfram Language you would have to write as a list:

m = {{12,19,28,34},{26,41,60,72}};

The implementation of Gene's method in Wolfram Language is simple. Just two lines:

rightReducingMatrix[m_] := Last[SmithDecomposition[m]]
smithDefactor[m_] := Take[Inverse[rightReducingMatrix[m]], MatrixRank[m]]

So the first thing that happens to [math]\displaystyle{ m }[/math] when you pass it in to smithDefactor[] is that it calls rightReducingMatrix[] on it. This will find the Smith decomposition (using a function built in to Wolfram Language), which gives you three outputs: the Smith normal form, flanked by its left and right reducing matrices. Gene asks only for the right reducing matrix, so we grab that with Last[]. So that's what the function on the first line, rightReducingMatrix[], does.

Then Gene asks us to invert this result and take its first [math]\displaystyle{ r }[/math] rows, where [math]\displaystyle{ r }[/math] is the rank of the temperament. Invert[] takes care of the inversion, of course. MatrixRank[m] gives the count of linearly independent rows to the mapping, AKA the rank, or count of generators in this temperament. In this case that's 2. And so Take[list, 2] simply returns the first 2 entries of the list.

Almost done! Except Gene not only defactors, he also calls for HNF, as we would, to achieve canonical (unique ID) form.

normalize[m_] := Last[HermiteDecomposition[m]]

Similar to the Smith Normal Form, we do a decomposition, which gives you the normal form plus some other bonus results. In this case we actually want the normal form itself, and it happens to be the last element in the result list. So putting it all together, we defactor and then normalize:

rightReducingMatrix[m_] := Last[SmithDecomposition[m]];
smithDefactor[m_] := Take[Inverse[rightReducingMatrix[m]], MatrixRank[m]];

normalize[m_] := Last[HermiteDecomposition[m]];

m = {{12,19,28,34},{26,41,60,72}};
normalize[smithDefactor[m]]

→ {{1,0,-4,-13},{0,1,4,10}}

And that result matches what Gene finds in that xen wiki article. Defactoring and normalizing is equivalent to canonicalization. 

New development: column Hermite defactoring

Here is the implementation for column Hermite defactoring:

hermiteUnimodular[m_]:=Transpose[First[HermiteDecomposition[Transpose[m]]]]
columnHermiteDefactor[m_]:=Take[Inverse[hermiteUnimodular[m]],MatrixRank[m]]

So this implementation begins by finding the unimodular matrix from a column Hermite decomposition. To make it a column Hermite decomposition, we first transpose the matrix. The decomposition in Wolfram returns two items - the unimodular matrix, and the input matrix in Hermite normal form, in that order — and in this case we actually want the unimodular matrix. So we take that with First[]. Then we Transpose[] it to in effect undo the transposition we did at the beginning.

The next step is to invert that matrix, which is doable because it is unimodular; a key property of unimodular matrices is that they are always invertible, and because their determinant is ±1, if they contain all integer entries, their inverse will also contain all integer entries (which it does, and we need it to).

Finally we take only the top [math]\displaystyle{ r }[/math] rows of this, where [math]\displaystyle{ r }[/math] is the rank of the original matrix. That's found with MatrixRank[m].

How/why it works

The basic idea is that the column Hermite decomposition leaves any common row factor the mapping might have had in the HNF part, while preserving in the unimodular part everything that's still meaningful about how the mapping works. So that's why we throw the column HNF away and keep the unimodular part. The rest of the algorithm is basically just "undoing" stuff so we get back to the structure of the matrix that we input.

So inverting is one of those "undo" type operations. To understand why, we have to understand the nature of this decomposition. What the Hermite decomposition does is return a unimodular matrix U and a Hermite normal form matrix H such that if you left-multiply your original matrix A by the unimodular matrix U you get the normal form matrix H, or in other words, UA = H. So, think of it this way. If A is what we input, and we want something sort of like A, but U is what we've taken, and U is multiplied with A in this equality to get H, where H is also kind of like A, then probably what we really want is something like U, but inverted.

Finally, we take only the top [math]\displaystyle{ r }[/math] rows, which again is an "undo" type operation. Here what we're undoing is that we had to graduate from a rectangle to a square temporarily, storing our important information in the form of this invertible square unimodular matrix temporarily, so we could invert it while keeping it integer, but now we need to get it back into the same type of rectangular shape as we put in. So that's what this part is for.

Various additional ways of thinking about how/why it works

Relationship with Smith defactoring

If you describe column Hermite defactoring as "column-Hermite inverse take-r-rows", the analogous way to describe Smith defactoring would be like "row-Hermite column-Hermite row-Hermite column-Hermite row-Hermite column-Hermite ... inverse take-r-rows". In other words, the nature of Smith decomposition is to essentially repeatedly Hermite decompose from either angle until you've achieved Smith normal form, which is wasteful and unnecessary in this context, when all that is required is a single column-Hermite decomposition. This helps explain why column Hermite defactoring is more performant in general than Smith defactoring, when code is run against thousands of examples at a time.

According to Wolfram, "the Smith decomposition can often be found by two iterations of the Hermite decomposition". This notion is echoed in the Sage docs, which read, "Use Hermite normal form twice to find an invertible matrix whose inverse transforms a matrix with the same row span as self to its saturation," remembered that saturation is the same as defactoring. The reason for the multiple applications of Hermite decomposition to achieve Smith normal form is that you won't necessarily get a diagonal matrix on the first go. But as we know from Smith defactoring, the center matrix of the Smith decomposition — the Smith normal form one — is not the target matrix, so its exact form is not necessary to achieve to accomplish defactoring.

Relationship with VEA

Another thought that might help congeal the notion of column Hermite defactoring for you is to use what you know about multimaps (AKA "wedgies"), in particular a) what they are, and b) how to defactor them. The answer to a) is that they are just the minor determinants (or "minors" for short) of rectangular matrices, or in other words, the closest thing rectangular matrices such as mappings have to a real determinant. And the answer to b) is that you simply extract the GCD of the entries in this list of minors. So if defactoring a list of minor determinants means dividing common factors out, then it should be little surprise that achieving a real determinant of ±1 is equivalent to defactoring, and thereby that leveraging the unimodularity of the other matrix produced by the Hermite decomposition should be valuable in this capacity.

Unimodular matrix size

One reason for doing a column Hermite decomposition on a mapping can be understood by comparing the sizes of the unimodular matrices. Matrices are often described as [math]\displaystyle{ m×n }[/math], where [math]\displaystyle{ m }[/math] is the row count and [math]\displaystyle{ n }[/math] is the column count. In the case of mappings it may be superior to use variable names corresponding to the domain concepts of rank [math]\displaystyle{ r }[/math], and dimension [math]\displaystyle{ d }[/math], i.e. to speak of [math]\displaystyle{ r×d }[/math] mappings. The key bit of info here is that — for non-trivial mappings, anyway — [math]\displaystyle{ d }[/math] is always greater than [math]\displaystyle{ r }[/math]. So a standard row-based Hermite decomposition, i.e. to the right, is going to produce an [math]\displaystyle{ r×r }[/math] unimodular matrix, while a column-based Hermite decomposition, i.e. to the bottom, is going to produce a [math]\displaystyle{ d×d }[/math] unimodular matrix. For example, 5-limit meantone has [math]\displaystyle{ r=2 }[/math] and [math]\displaystyle{ d=3 }[/math], so a standard row-based Hermite decomposition is going to produce a unimodular matrix that is only 2×2, while the column-based Hermite decomposition will produce one that is 3×3. With [math]\displaystyle{ d\gt r }[/math], it's clear that the column-based decomposition in general will always produced the larger unimodular matrix. In fact, the row-based decomposition is too small to be capable of enclosing an amount of entries equal to the count of entries in the original mapping, and therefore it could never support preserving the entirety of the important information from the input (in terms of our example, a 3×3 matrix can hold a 2×3 matrix, but a 2×2 matrix cannot).

By hand

In an effort to demystify the effects of column Hermite defactoring, let's walk though an example manually.

First we need to learn how to perform its two building blocks by hand:

1. Hermite decomposition
2. inversion

After we know how to do these two things individually, we'll learn how to tweak them and assemble them together in order to perform a complete column Hermite defactoring.

Fortunately, both of these two processes can be done using a technique you may already be familiar with if you've learned how to calculate the null-space of a mapping by hand (as demonstrated here):

1. augmenting your matrix with an identity matrix
2. performing elementary row or column operations until a desired state is achieved

Hermite decomposition by hand

Let's do a Hermite decomposition example first. We begin with the mapping for the temperament 12&26bbb, which looks like [⟨12 19 28] ⟨26 43 60]⟩, or as a matrix:

[math]\displaystyle{ \left[ \begin{array} {rrr} 12 & 19 & 28 \\ 26 & 43 & 60 \\ \end{array} \right] }[/math]

Then we augment it with an identity matrix. However, unlike with the method for finding the null-space, we do not augment it on the bottom, but to the right:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 12 & 19 & 28 \\ 26 & 43 & 60 \\ \end{array} & \rule[-5mm]{0.375mm}{12mm} & \begin{array} {r} 1 & 0 \\ 0 & 1 \\ \end{array} \end{array} \right] }[/math]

Now we begin applying elementary row operations until the part on the left is in Hermite Normal Form. If you need to review the definition of HNF and its constraints, you can find more detail here. The quick and dirty is:

1. all pivots > 0
2. all entries in pivot columns below the pivots = 0
3. all entries in pivot columns above the pivots ≥ 0 and strictly less than the pivot

One special thing about computing the HNF is that we're not allowed to use all elementary operations; in particular we're not allowed to multiply (or divide) rows. Our main technique, then, will be adding or subtract rows from each other. This, of course, includes adding or subtracting multiples of rows from each other, because doing so is equivalent to performing those additions or subtractions one at a time (note that adding or subtracting multiples of rows from each other is significantly different than simply multiplying a row by itself).

So let's begin by subtracting the 1st row from the 2nd row, and let's do it 2 times, because we can see that would get the pivot of the 2nd row pretty close to 0, which is where we're trying to get it, per the 2nd HNF constraint above.

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 12 & 19 & 28 \\ 2 & 5 & 4 \\ \end{array} & \rule[-5mm]{0.375mm}{12mm} & \begin{array} {r} 1 & 0 \\ -2 & 1 \\ \end{array} \end{array} \right] }[/math]

Okay. We can see now that if we subtract 6 times the 2nd row back from the 1st row now, we'll create a 0 in the first column. It's not in the bottom left where we need it, but that's no big deal; reordering the rows is an allowed row operation. So let's do that subtraction:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 0 & -11 & 4 \\ 2 & 5 & 4 \\ \end{array} & \rule[-5mm]{0.375mm}{12mm} & \begin{array} {r} 13 & -6 \\ -2 & 1 \\ \end{array} \end{array} \right] }[/math]

And then reorder the rows:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 2 & 5 & 4 \\ 0 & -11 & 4 \\ \end{array} & \rule[-5mm]{0.375mm}{12mm} & \begin{array} {r} -2 & 1 \\ 13 & -6 \\ \end{array} \end{array} \right] }[/math]

We're actually quite close to done! All we need to do is flip the signs on the 2nd row. But wait, you protest! Isn't that multiplying a row by -1, which we specifically forbade? Well, sure, but that just shows we need to clarity what we're concerned about, which is essentially enfactoring. Multiplying by -1 does not change the GCD of the row, where multiplying by -2 or 2 would. Note that because the process for taking the HNF forbids multiplying or dividing, it will never introduce enfactoring where was there was none previously, but it also does not remove enfactoring that is there.

Perhaps another helpful way of thinking about this is that multiplying the row by -1 does not alter the potential effects this row could have being added or subtracted from other rows. It merely swaps addition and subtraction. Whereas multiplying the row by any integer with absolute value greater than 1 would affect the potential effects this row could have being added or subtracted from other rows: it would limit them.

So, let's do that sign flip:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 2 & 5 & 4 \\ 0 & 11 & -4 \\ \end{array} & \rule[-5mm]{0.375mm}{12mm} & \begin{array} {r} -2 & 1 \\ -13 & 6 \\ \end{array} \end{array} \right] }[/math]

And we're done! Let's confirm though.

1. all pivots > 0? Check. The 1st row's pivot is 2 and the 2nd row's pivot is 11.
2. all entries in pivot columns below the pivots = 0? Check. This only applies to one entry — the bottom right one, below the 1st row's pivot — but it is indeed 0.
3. all entries in pivot columns above the pivots ≥ 0 and strictly less than the pivot? Check. Again, this only applies to one entry — the center top one, above the 2nd row's pivot of 11 — but it is 5, and 5 is indeed non-negative and < 11.

And so, we have performed the Hermite decomposition. The matrix to the left of the augmentation line — the one in place of our original matrix — is that original matrix in HNF:

[math]\displaystyle{ \left[ \begin{array} {rrr} 2 & 5 & 4 \\ 0 & 11 & -4 \\ \end{array} \right] }[/math]

And the matrix to the right of the augmentation line is the other output of the Hermite decomposition: a unimodular matrix with a special property.

[math]\displaystyle{ \left[ \begin{array} {rrr} -2 & 1 \\ -13 & 6 \\ \end{array} \right] }[/math]

This special property is that if you take the original matrix and left multiply it by this unimodular matrix, you will get the HNF.

[math]\displaystyle{ \begin{array} {l} \left[ \begin{array} {rrr} -2 & 1 \\ -13 & 6 \\ \end{array} \right] & × & \left[ \begin{array} {r} 12 & 19 & 28 \\ 26 & 43 & 60 \\ \end{array} \right] & = & \left[ \begin{array} {r} 2 & 5 & 4 \\ 0 & 11 & -4 \\ \end{array} \right] \end{array} }[/math]

And that's all there is to the Hermite decomposition.

Inversion by hand

Now let's take a look at how to do inversion by hand. The first thing to note is that this process only works for rectangular matrices. So you will not be using on non-trivial mappings or comma bases directly. But, as you know, there is a useful application for this process on the unimodular matrix which is the other result of the Hermite decomposition than the HNF, and unimodular matrices are always square.

Here's a random example matrix (well, one I stole from a quick web search, anyway):

[math]\displaystyle{ \left[ \begin{array} {rrr} 3 & -2 & 4 \\ 1 & 0 & 2 \\ 0 & 1 & 0 \\ \end{array} \right] }[/math]

The first step is to augment it. Similar to the Hermite decomposition process, we augment it to the right:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 3 & -2 & 4 \\ 1 & 0 & 2 \\ 0 & 1 & 0 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \end{array} \right] }[/math]

Our goal now is to use elementary row operations until the original matrix — the one to the left of the augmentation line — is an identity matrix. At that point, the matrix on the right side of the augmentation line — the one that started out as an identity matrix — will be the inverse of the original matrix. I don't know about you, but for me, this relationship was instantly intuitive and memorable, and I'm super glad I learned how to this one by hand!

As our first step, let's rearrange the rows of the matrix. Just some obvious-looking moves (that probably won't backfire) to get us superficially closer to the identity matrix on the left:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 1 & 0 & 2 \\ 0 & 1 & 0 \\ 3 & -2 & 4 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{array} \end{array} \right] }[/math]

Okay, now let's target the bottom-right entry. How can we make that 3 into a 0? Let's subtract the 1st row from the 3rd row 3 times:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} \color{blue}1 & \color{blue}0 & \color{blue}2 \\ 0 & 1 & 0 \\ \color{red}0 & \color{red}-2 & \color{red}-2 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} \color{blue}0 & \color{blue}1 & \color{blue}0 \\ 0 & 0 & 1 \\ \color{red}1 & \color{red}-3 & \color{red}0 \\ \end{array} \end{array} \right] }[/math]

Okay, let's next target the bottom-center entry. How can we make that -2 into a 0? Let's add the 2nd row to the 3rd row 2 times:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 1 & 0 & 2 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{red}0 & \color{red}0 & \color{red}-2 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} 0 & 1 & 0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 \\ \color{red}1 & \color{red}-3 & \color{red}2 \\ \end{array} \end{array} \right] }[/math]

Next, let's target the top-right entry, making that a 0 by adding the 3rd row to the 1st row:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} \color{red}1 & \color{red}0 & \color{red}0 \\ 0 & 1 & 0 \\ \color{blue}0 & \color{blue}0 & \color{blue}-2 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} \color{red}1 & \color{red}-2 & \color{red}2 \\ 0 & 0 & 1 \\ \color{blue}1 & \color{blue}-3 & \color{blue}2 \\ \end{array} \end{array} \right] }[/math]

Finally, we just need to divide the 3rd row by -2. Yes, unlike with the Hermite decomposition, all elementary row operations are permitted, including multiplying or dividing rows. And in this case there's no restrictions against non-integers (which we didn't even explicitly mention when doing the HNF, but yes, HNF requires integers). So here's where we end up:

[math]\displaystyle{ \left[ \begin{array} {l} \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \color{red}0 & \color{red}0 & \color{red}1 \\ \end{array} & \rule[-7.5mm]{0.375mm}{18mm} & \begin{array} {r} 1 & -2 & 2 \\ 0 & 0 & 1 \\ \color{red}-\frac12 & \color{red}\frac32 & \color{red}-1 \\ \end{array} \end{array} \right] }[/math]

As with the Hermite decomposition, we have a convenient way to check our work at the end, which involves matrix multiplication. With Hermite, we verified that left-multiplying our original matrix by the unimodular matrix resulted in the HNF. With inversion, we verify that left-multiplying our original matrix by the inverse results in the identity matrix. And indeed:

[math]\displaystyle{ \begin{array} {1} \left[ \begin{array} {rrr} 3 & -2 & 4 \\ 1 & 0 & 2 \\ 0 & 1 & 0 \\ \end{array} \right] & × & \left[ \begin{array} {rrr} 1 & -2 & 2 \\ 0 & 0 & 1 \\ -\frac12 & \frac32 & -1 \\ \end{array} \right] & = & \left[ \begin{array} {rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

I chose this matrix specifically to demonstrate the importance of the unimodularity of the other matrix produced by the Hermite decomposition. A unimodular matrix is defined by having a determinant of ±1. And what does this have to do with inverses? Well, take a look at the determinant of our original matrix here, [⟨3 -2 4] ⟨1 0 2] ⟨0 1 0]⟩. It's 2. The determinant of an invertible matrix will tell you what the LCM of all the denominators in the inverse will be And so, the fact that the other matrix produced by the Hermite decomposition is unimodular means that not only is it invertible, if it has only integer terms (which it will, being involved in HNF), then its inverse will also have only integer terms. And this is important because the inverse of a Hermite unimodular matrix is just one step away from the defactored form of an input matrix.

Putting it all together

In the Wolfram Language algorithm described above, the input matrix is first transposed and then Hermite decomposed. In fact, this is due to a limitation of the built-in HermiteDecomposition[] function in Wolfram Language. The HNF is well understood both in its more common and default row-style as well as a column-style, so it might be expected for Wolfram Language to provide an option for the HermiteDecomposition[] function to perform it by columns. Alas, it does not. So the transposition our code does is a workaround for this lack.

When doing a column-style Hermite decomposition by hand, we have two options:

1. Mimic this workaround that we're doing in the code: transpose the matrix, and then do a Hermite decomposition as demonstrated above: augment to the right and perform row operations;
2. Augment the matrix to the bottom, and then use elementary column operations instead of elementary row operations (such that it looks more similar to the process for computing the null-space by hand).

Here, we'll be demonstrating the process using the first option, because we might as well follow the same approach as the code unless we have a compelling reason not to. And we don't! If we were to follow the second option — rotating everything 90 degrees — we'd have to rewire our brains to recognize matrices in HNF but rotated 90 degrees, which is certainly harder than just transposing a matrix 90 degrees and then treating it the same way with respect to the complexities of Hermite decomposition as we've already become accustomed to.

So, while it's a silly example, let's suppose we want to defactor the mapping [⟨6 5 4] ⟨4 -4 1]⟩. Spoiler alert: it is 11-enfactored:

[math]\displaystyle{ \left[ \begin{array} {rrr} 6 & 5 & -4 \\ 4 & -4 & 1 \\ \end{array} \right] }[/math]

Our first step is to transpose it:

[math]\displaystyle{ \left[ \begin{array} {rrr} 6 & 4 \\ 5 & -4 \\ -4 & 1 \\ \end{array} \right] }[/math]

And now we're going to augment it to the right, so we can do the first step of the Hermite decomposition. But we're actually going to go a bit further. We're going to go ahead and augment it to the right and also augment the augmenting matrix to the bottom, because that's where we're going to perform the next step, which is the inversion. We learned inversion using augmentation to the right, but remember: everything we're doing here is transposed! So augmenting to the bottom is the correct thing to do there. When we're all done, we'll transpose one more time to undo it. (In the Wolfram Language code it was more natural to transpose things between the Hermite decomposition and the inversion, but here I think the process is better illustrated with this rotated-L-shape structure.)

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 6 & 4 \\ 5 & -4 \\ -4 & 1 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

Alright. So our first goal is to get the top-left matrix into HNF. Let's subtract the 2nd row from the 1st row — that will get us a 1 in the top-left entry, which is what we want if we can.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} \color{red}1 & \color{red}8 \\ \color{blue}5 & \color{blue}-4 \\ -4 & 1 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{red}1 & \color{red}-1 & \color{red}0 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \\ 0 & 0 & 1 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

Now let's subtract the 1st row from the 2nd row 5 times. That'll get us a 0 below that first pivot, which is what we need.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} \color{blue}1 & \color{blue}8 \\ \color{red}0 & \color{red}-44 \\ -4 & 1 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{blue}1 & \color{blue}-1 & \color{blue}0 \\ \color{red}-5 & \color{red}6 & \color{red}0 \\ 0 & 0 & 1 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

Now let's add the 1st row to the 3rd row 4 times. That'll allow us to achieve all 0's below the first pivot.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} \color{blue}1 & \color{blue}8 \\ 0 & -44 \\ \color{red}0 & \color{red}33 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{blue}1 & \color{blue}-1 & \color{blue}0 \\ -5 & 6 & 0 \\ \color{red}4 & \color{red}-4 & \color{red}1 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

Now let's add the 3rd row to the 2nd row. We can see that if we do that, we'll simplify their relationship. If it's not clear now, it'll be clear in the next step.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ \color{red}0 & \color{red}-11 \\ \color{blue}0 & \color{blue}33 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & -1 & 0 \\ \color{red}-1 & \color{red}2 & \color{red}1 \\ \color{blue}4 & \color{blue}-4 & \color{blue}1 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

So now we can add the 2nd row to the 3rd row 3 times, and that'll get the entry below the 2nd pivot to be 0.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ \color{blue}0 & \color{blue}-11 \\ \color{red}0 & \color{red}0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & -1 & 0 \\ \color{blue}-1 & \color{blue}2 & \color{blue}1 \\ \color{red}1 & \color{red}2 & \color{red}4 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

We can flip the signs of the second row, because we need pivots to be positive.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ \color{red}0 & \color{red}11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & -1 & 0 \\ \color{red}1 & \color{red}-2 & \color{red}-1 \\ 1 & 2 & 4 \\ \hline 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \end{array} }[/math]

And we've completed the first step! The original matrix is now in HNF. So the next step is to take the other matrix we've been working on — the unimodular one from the Hermite decomposition — and invert it. Again, since we're in a transposed state, we're going to do the by-hand inversion technique, but to the bottom using elementary column operations rather than to the right using elementary row operations.

For our first step, let's add the 1st column to the 2nd column. That will get us a 0 in the top-center entry. Remember, we're trying to get the top-right matrix to look like an identity matrix.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{blue}1 & \color{red}0 & 0 \\ \color{blue}1 & \color{red}-1 & -1 \\ \color{blue}1 & \color{red}3 & 4 \\ \hline \color{blue}1 & \color{red}1 & 0 \\ \color{blue}0 & \color{red}1 & 0 \\ \color{blue}0 & \color{red}0 & 1 \\ \end{array} \right] \end{array} }[/math]

Now let's add the new 2nd column back to the 1st column. This will get the entry in the center-left to be 0.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{red}1 & \color{blue}0 & 0 \\ \color{red}0 & \color{blue}-1 & -1 \\ \color{red}4 & \color{blue}3 & 4 \\ \hline \color{red}2 & \color{blue}1 & 0 \\ \color{red}1 & \color{blue}1 & 0 \\ \color{red}0 & \color{blue}0 & 1 \\ \end{array} \right] \end{array} }[/math]

Now let's subtract the 2nd column from the 3rd column. This is sweet because it gets the center-right entry to be 0 as well as the bottom-right entry to be 1. A twofer! Plus it gives us our first column which has all zeros except for one row, which gives us the power to affect the entry in that row of other columns without messing up any of the other rows of those columns.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & \color{blue}0 & \color{red}0 \\ 0 & \color{blue}-1 & \color{red}0 \\ 4 & \color{blue}3 & \color{red}1 \\ \hline 2 & \color{blue}1 & \color{red}-1 \\ 1 & \color{blue}1 & \color{red}-1 \\ 0 & \color{blue}0 & \color{red}1 \\ \end{array} \right] \end{array} }[/math]

Okay. So if we now subtract the 3rd column from the 1st column 4 times, we can get the bottom-left entry to be a 0.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} \color{red}1 & 0 & \color{blue}0 \\ \color{red}0 & -1 & \color{blue}0 \\ \color{red}0 & 3 & \color{blue}1 \\ \hline \color{red}6 & 1 & \color{blue}-1 \\ \color{red}5 & 1 & \color{blue}-1 \\ \color{red}-4 & 0 & \color{blue}1 \\ \end{array} \right] \end{array} }[/math]

And now we can subtract the 3rd column from the 2nd column 3 times, so we can get the bottom-center entry to be a 0.

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & \color{red}0 & \color{blue}0 \\ 0 & \color{red}-1 & \color{blue}0 \\ 0 & \color{red}0 & \color{blue}1 \\ \hline 6 & \color{red}4 & \color{blue}-1 \\ 5 & \color{red}4 & \color{blue}-1 \\ -4 & \color{red}-3 & \color{blue}1 \\ \end{array} \right] \end{array} }[/math]

As our last step to achieve an identity matrix in the top-right matrix, let's just flip the signs of the 2nd column:

[math]\displaystyle{ \begin{array} {l} \begin{array} {l} \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right. \\ \begin{array} {l} \\ \\ \\ \end{array} \end{array} & \rule[2.5mm]{0.375mm}{18mm} & \left. \begin{array} {r} 1 & \color{red}0 & 0 \\ 0 & \color{red}1 & 0 \\ 0 & \color{red}0 & 1 \\ \hline 6 & \color{red}-4 & -1 \\ 5 & \color{red}-4 & -1 \\ -4 & \color{red}3 & 1 \\ \end{array} \right] \end{array} }[/math]

And so we've inverted the Hermite unimodular matrix. That's our result in the bottom-right matrix, isolated here:

[math]\displaystyle{ \left[ \begin{array} {rrr} 6 & -4 & -1 \\ 5 & -4 & -1 \\ -4 & 3 & 1 \\ \end{array} \right] }[/math]

But we're not quite to our defactored result. We're very close though! All we've got to do now is take that result and transpose it, to get us out of the transposed state we've been in (in other words, flip every entry across the main diagonal, running from the top-left entry to the bottom-right entry):

[math]\displaystyle{ \left[ \begin{array} {rrr} 6 & 5 & -4 \\ -4 & -4 & 3 \\ -1 & -1 & 1 \\ \end{array} \right] }[/math]

And we take from this thing the top [math]\displaystyle{ r }[/math] rows, where [math]\displaystyle{ r }[/math] is the rank of the input matrix, which in this case is 2:

[math]\displaystyle{ \left[ \begin{array} {rrr} 6 & 5 & -4 \\ -4 & -4 & 3 \\ \end{array} \right] }[/math]

And that's all there is to defactoring!

Note that this is not yet the canonical form. Remember that to achieve canonical form, we still have to take this result and get it into HNF. We won't work through that here, though if you'd like to practice by-hand Hermite decomposition, this would be a perfect example to try it on! The result you should end up with is [⟨2 1 -1] ⟨0 2 -1]⟩.

But what have we accomplished here, really? You may well feel underwhelmed by this matrix's transformation from [⟨6 5 -4] ⟨4 -4 1]⟩ to [⟨6 5 -4] ⟨-4 -4 3]⟩. It seems barely to have even changed!

Well, the difference becomes clearer when we compare the HNF of the original matrix, which is [⟨2 9 -5] ⟨0 22 -11]⟩, a clearly 11-enfactored mapping. One thing that's cool about performing this defactoring process by hand is that you can clearly see any common factor that you've removed as a result: all you have to do is look at the pivots of the HNF of the original matrix that you left behind, which in this case was:

[math]\displaystyle{ \left[ \begin{array} {rrr} 1 & 8 \\ 0 & 11 \\ 0 & 0 \\ \end{array} \right] }[/math]

The pivots are 1 and 11, so that 11 tells us that we had a common factor of 11. You could say that the HNF is useful for identifying common factors, but not for removing them. But if you leave them behind in the column-style HNF, the information that is retained in the unimodular matrix which is the other product of the Hermite decomposition, is enough to preserve everything important about the temperament, to get you back to where you started via an inverse and a trimming of extraneous rows.

Other defactoring methods

When in development on an ideal defactoring method — the effort which culminated in column Hermite defactoring — Dave and Douglas experimented on other methods:

• SAD defactoring
• MADAM defactoring

Canonical comma bases

Canonical form is not only for mappings; comma bases may also be put into canonical form. The only difference is that they must be put in an "antitranspose sandwich", or in other words, antitransposedonce at the beginning, and then antitransposed again at the end.

For example, suppose we have the comma basis for septimal meantone:

[math]\displaystyle{ \left[ \begin{array} {rrr} -4 & 1 \\ 4 & 2 \\ -1 & -3 \\ 0 & 1 \\ \end{array} \right] }[/math]

Note that the interval vectors are columns when put into matrix form like this.

So now we antitranspose, or in other words, transpose the matrix but instead of across its main diagonal (top-left to bottom-right) as with the traditional transpose, across its antidiagonal (top-right to bottom-left).

[math]\displaystyle{ \begin{array} {l} \left[ \begin{array} {rrr} \colorbox{skyblue}{-4} & \colorbox{yellow}{1} \\ \colorbox{yellow}{4} & \colorbox{pink}{2} \\ \colorbox{springgreen}{-1} & \colorbox{pink}{-3} \\ \colorbox{springgreen}{0} & \colorbox{pink}{1} \\ \end{array} \right] & → & \left[ \begin{array} {rrr} \colorbox{pink}{1} & \colorbox{pink}{-3} & \colorbox{pink}{2} & \colorbox{yellow}{1} \\ \colorbox{springgreen}{0} & \colorbox{springgreen}{-1} & \colorbox{yellow}{4} & \colorbox{skyblue}{-4} \\ \end{array} \right] \end{array} }[/math]

This has the effect of both reversing the entries within each interval, as well as reversing the order of the intervals themselves. The purpose of these reversals is so that when the HNF tries to put all the zeros in the bottom-left corner, it gravitates them toward where we want them: the higher primes, and commas that will be earlier in the list after the second antitranspose.

Now we can defactor and HNF this as if it were a mapping.

[math]\displaystyle{ \left[ \begin{array} {rrr} 1 & 0 & -10 & -13 \\ 0 & 1 & -4 & 4 \\ \end{array} \right] }[/math]

Finally we antitranspose again:

[math]\displaystyle{ \begin{array} {l} \left[ \begin{array} {rrr} \colorbox{pink}{1} & \colorbox{pink}{0} & \colorbox{pink}{-10} & \colorbox{yellow}{-13} \\ \colorbox{springgreen}{0} & \colorbox{springgreen}{1} & \colorbox{yellow}{-4} & \colorbox{skyblue}{4} \\ \end{array} \right] & → & \left[ \begin{array} {rrr} \colorbox{skyblue}{4} & \colorbox{yellow}{13} \\ \colorbox{yellow}{-4} & \colorbox{pink}{-10} \\ \colorbox{springgreen}{1} & \colorbox{pink}{0} \\ \colorbox{springgreen}{0} & \colorbox{pink}{1} \\ \end{array} \right] \end{array} }[/math]

And there's our canonical comma basis.