Kite's thoughts on 41edo Lattices

Lattices

Lattices are a great tool for exploring just intonation (aka JI) and also near-just music in the larger edos.

The 5-limit (ya) Lattice

This lattice uses ups and downs notation:

The middle row is a chain of 5ths. Moving one step to the right (aka fifthwards) adds a 5th, and one step to the left (fourthwards) adds a 4th. Moving diagonally right-and-up (the 1:00 direction) adds a downmajor 3rd, 5/4. This yoward step adds prime 5. Moving guward left-and-down subtracts prime 5. Since moving 5thwards/4thwards adds/subtracts prime 3, every 5-limit monzo translates directly to a series of sideways and diagonal steps, and every octave-reduced 5-limit ratio appears exactly once in the lattice. Thus the lattice is a "map" of all possible notes.

Every interval appears in the lattice as a vector. For example a major 7th is one step fifthward and one step yoward, making a vector in the 2:00 direction that spans two triangles.

The middle row is the plain row. The row immediately above it is the down row. Then double-down, triple-down, etc. Why does one go up to the down row? For a full explanation of this and lattices in general, see chapter 1.3 of Kite's book, Alternative Tunings: Theory, Notation and Practice.

If this were just intonation, the lattice would extend infinitely in all directions. But because this is 41-equal, the double-down row could be rewritten as a double-up row. For example, vvB = ^^Bb. And triple-down notes would in practice almost always written as up notes. So the lattice wraps around on itself, like a world map in which the western tip of Alaska appears on both the far right and the far left. More on this later.

Every chord type has a certain shape. Downmajor aka 5-over or yo chords such as D vF# A appear as upward-pointing triangles. Upminor aka 5-under or gu chords are downward-pointing triangles. The downmajor7 chord is two adjacent triangles, as is the upminor7 chord. The downmajor6 chord has the same shape as the upminor7 chord, which tells you that they are chord homonyms (same notes, different roots).

Chord progressions can be mapped out on the lattice as a series of chord shapes. Often two adjacent chords have a common tone, and the progression "walks" around the lattice. If there are no common tones, the progression "jumps" from one area to another. Often there are several different places to jump. More on this later.

The 7-limit (yaza) lattice

Moving zowards in the 2:00 direction from the D exactly in the middle to the nearby vC adds 7/4. This direction can be thought of as a third dimension, making the down7 chord D vF# A vC be a tetrahedron protruding upwards from the page. Likewise the upminor6 chord D ^F A ^B is a tetrahedron sinking down into the page. The lattice has three layers. One layer is the original 5-limit lattice. All the notes that protrude upwards form a 2nd layer, and all the sinking notes make the 3rd layer. Whereas the 5-limit lattice lets you move three steps in the yoward direction, this 7-limit lattice only lets you move one step zoward. We will fix this in Lattices Part II.

In the 5-limit lattice, each note has a unique name. To find vvD#, go to the double-down row and look among the notes with sharps. But in the 7-limit lattice, multiple notes have the same name. In just intonation, they would sound different, but in 41-equal they are identical.

Commas

A comma is a just intonation ratio that is a narrow interval of less than (roughly) 50¢. In 41edo (or any edo for that matter), a comma is mapped to a small number of edosteps, usually 0 or 1, occasionally 2. The technical term for a comma that maps to 0 edosteps is vanishing comma. On the Kite guitar, mapping to 0, 1 or 2 edosteps can be called a no-fret, half-fret or one-fret comma.

5-limit (ya) commas

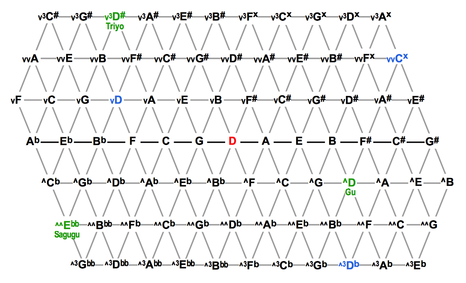
Certain notes are colored red and green for emphasis. (The color choice is arbitrary.) The green notes are all half a fret sharper than the red D. The vector from the red D to any of these green notes is a half-fret comma. The three half-fret commas are named via color notation, and the name tells you which row it's on: Triyo is 3 rows up, Gu is one row down, and Sagugu is two rows down.

The most important comma historically is the Gu comma, with ratio 81/80. Consider the progression Im - bIII - bVII - IV - Im. On the lattice, it becomes D^m - ^Fv - ^Cv - ^Gv - ^D^m, and it walks you from D to ^D. This is called a comma pump. Such pumps are a major issue in just intonation. On the Kite guitar fretboard, this comma pump walks you fifthwards, which is towards the nut.

The progression I - vi - ii - V - I becomes Dv - vB^m - vE^m - vAv - vDv, which is a descending pump that walks you towards the bridge.

The Gu comma vanishes in meantone temperaments like 12-equal, and you can play such progressions without worrying. But when translating songs to 41-equal, one has to deal with Gu over and over, usually with a pitch shift.

The other commas can be pumped too, but they rarely are. Sagugu is also a no-fret comma in 12-equal. So you can sit down with a 12-equal guitar or keyboard and play a progression that walks to (or from) Sagugu, and you'll have done something quite unique!

The one-fret commas such as D to vvD# (Yoyo) aren't included because such commas are too big to fudge. The zero-fret commas would be included, but they are too remote to fit on this lattice. However they can be deduced from the green notes, because from one green note to another is a no-fret comma. For example, from Sagugu to Gu is the Layo comma. If we imagine a vector running from Sagugu to Gu, and then slide that vector over to start at the red D, we can see that Layo is on the down row, a few steps past the righthand edge. If the lattice were bigger, there would be a red vC# there. This is another comma that 12-equal tempers out, but is very rarely pumped.

There are two more remote no-fret commas. From Sagugu to Triyo is the Laquinyo comma. From Gu to Triyo is the Saquadyo comma. Neither of these vanish in 12-equal. Saquadyo is the comma that equates the double-up row with the double-down row.

7-limit (yaza) commas

This lattice introduces two no-fret commas, Saruyo and Ruyoyo. Both are reasonably close and fairly pumpable. The unlabeled red notes are just the descending versions of these two commas. Since the comma maps to zero frets, there is no difference in 41-equal between an ascending comma pump and a descending one, and both versions can be treated as the same.

An example of a Saruyo pump is I Will Survive.

You can play such progressions without worrying. Lame joke: without fretting, that's why it's called a no-fret comma!

This lattice also introduces the green Ru comma, very important because it's so nearby. Like Gu, this one...

Lattices Part II

The Full Yaza Lattice

As previously noted, the 7-limit lattice is limited to only three layers, zo = 7-over, ru = 7-under and noza = no-7s. This is rather limiting. For example, any comma with a 7-exponent greater than 1 or less than -1 won't appear in this lattice, e.g. 50/49 or 49/48. The solution to this is to assume the Bizozogu microcomma is tempered out. This comma is only 0.7¢ and is nearly impossible to hear. Strangely enough, it doesn't vanish in 12-equal, although it does in 41-equal! This comma equates the layer above zo with the one below ru. To fit all 4 layers onto one plane, the lattice becomes rectangular. The gray lines that form triangles are still there, but the notes inside the triangles are shifted slightly to make a straight row. (Actually only nearly straight, to preserve readability.) In addition, unnamed dots have been added to the other rows. These dots form the 4th layer.

The previous lattice was 3-D, but this one can be viewed as both 3-D and 2-D. To navigate this lattice, one could step as before 4thwd/5thwd, yoward/guward and zoward/ruward. But as a 2-D lattice, one steps rightward/leftward and upward/downward. Each horizontal step is one-half as long as a triangle-side. Thus on the middle row, from D to A is two rightward steps. Thus one rightward step is half a 5th, i.e. a neutral 3rd. From D up to G# is a vertical step. Thus one upward step is just over half an octave, and two upward steps octave-reduces to a half-fret comma.

Before, there was a one-to-one correspondence between notes in the lattice and JI ratios. But now, any ratio can have the Bizozogu comma added to it and that new ratio will map to the same spot in the lattice. For example, the unnamed dot between D and A represents both 60/49 and 49/40. As the former, it's the 6th of a G#^m6 chord, and would be spelled ^E#. As the latter, it's the 7th of an Abv7 chord, and would be spelled vGb. It could also be spelled ^^F or vvF#. This is why the dots are unnamed!

Here's this new lattice with commas marked:

The commas are unnamed because one spot on the lattice represents multiple commas. For example, the green dot directly above the red D in the middle represents both the Zozo and Biruyo commas.

Using 2-D steps, the Ruyoyo comma is now 5 rightward steps and 3 upwards steps. Using 3-D steps, from the red D to the red vCx has a familiar shape: two 5thwd steps, two yoward stets and a ruward step. From the red ^Ebb to the red D has a similar shape.

But notice the shape of the interval between the two green notes directly above the red D to the red vCx. it's one and a half 5thwd steps, one yoward step and one zoward step. From the green ^D (the Ru comma in the 4th lattice) to the green dot is the same steps. So the 2-D shape of the comma doesn't change, but the 3-D shape does. When you're tracing a chord progression on the full yaza lattice, it's very helpful to be able to spot the Ruyoyo comma in these different shapes. Something similar happens with the Ru comma.

The 11-limit (yazala) and 13-limit (yazalatha) Lattice

This lattice can also be applied to higher prime limits by assuming the Lulu and Thuthu commas. These are not microcommas, and are fairly audible at 8¢ and 17¢ respectively. Thus this wouldn't be a very accurate lattice for JI. But this lattice works well for 41-equal because both commas are no-fret commas. The rightward step becomes both 11/9 and 27/22, as well as 39/32 and 16/13, all neutral 3rds.

Commas Part II

The Kite guitar fretboard is made up of alternating rainbow zones and off zones. Playing a Gu or Ru pump on the Kite guitar forces one to either shift a pitch or walk into the off zone. Going into the off zone makes the tonic drift sharp or flat by half a fret. But playing a Saruyo pump forces one to walk up the neck clear through the off zone into the next rainbow zone. The tonic drifts flat and then sharp!

We can call Saruyo a walk-once comma, and Ru and Gu walk-halfway commas. All no-fret commas are no-walk, walk-once, walk-twice, etc. All half-fet commas are walk-halfway, walk-one-and-a-half, etc.

Rank and Co-rank

5-limit JI is a rank-3 tuning, and any edo is a rank-1 tuning. Thus any two linearly independent (i.e. non-redundant) commas suffice to reduce 5-limit JI to an edo. The choice of which two commas determines which edo we end up in.