Talk:Tenney–Euclidean tuning

This page also contains archived Wikispaces discussion.

Crazy math theory's dominating the article

Anybody can read this article in its current shape and learn how to derive the TE tuning, TE generators, etc.? I can't. How I learned it was by coming up with the idea of RMS-error tuning, posting it on reddit and get told that was actually called TE tuning.

That said, TE tuning is an easy problem if you break it down this way.

What's the problem?

It's a least squares problem of the following linear equations:

[math]\displaystyle{ (AW)^\mathsf{T} \vec{g} = W\vec{p} }[/math]

where A is the known mapping of the temperament, g the column vector of each generators in cents, p the column vector of targeted intervals in cents, usually prime harmonics, and W the weighting matrix.

This is an overdetermined system saying that the sum of (AW)^T_ij steps of generator g_j for all j equals the corresponding interval (Wp)_i.

How to solve it?

The pseudoinverse is a common means to solve least square problems.

We don't need to document what a pseudoinverse is, at least not in so much amount of detail, cuz it's not a concept specific in tuning, and it's well documented on wikipedia. Nor do we need to document why pseudoinverses solve least square problems. Again, that's not a question specific in tuning.

The only thing that matters is to identify the problem as a least square problem. The rest is nothing but manual labor.

I'm gonna try improving the readability of this article by adding my thoughts and probably clear it up. FloraC (talk) 18:52, 24 June 2020 (UTC)

Update: the page is clear enough now.

The standard way to write the equation is:

[math]\displaystyle{ G(AW) = J_0 W }[/math]

The targeted interval list is known as JIP and is denoted J₀ here. The main difference from my previous comment is that the generator list and the JIP are presented as row vectors. It can be further simplified to

[math]\displaystyle{ GV = J }[/math]

which is pretty clearly displayed in the article. FloraC (talk) 17:39, 16 December 2021 (UTC)

Damage, not error?

The article says, "Just as TOP tuning minimizes the maximum Tenney-weighted (L1) error of any interval, TE tuning minimizes the maximum TE-weighted (L2) error of any interval." But shouldn't it be "damage", not "error"? As far as I understand it, there would be no way to minimize the maximum error of any interval under a tuning, because you could always find a more complex interval with more error; minimaxing only makes sense for damage, which scales proportionally with the complexity of the interval. Or am I misunderstanding these concepts? --Cmloegcmluin (talk) 16:50, 28 July 2021 (UTC)

Ah, I think I see. "Damage" may be a bit of an outdated term. It's what Paul Erlich uses in his Middle Path paper. But it means error weighted (divided) by the Tenney height, which is equivalent to the L1 norm, and so "Tenney-weighted (L1) error" is the same thing as damage. And "TE-weighted (L2) error" means error weighted by the TE height, which is equivalent to the L2 norm, so it's similar to damage. --Cmloegcmluin (talk) 19:04, 28 July 2021 (UTC)

Corrections:

* The term damage is not outdated.

* My quotations from the article are out of date. They show "L1" and "L2" in parenthesis, which implies that they "Tenney-weighted error" is the same thing as "L1 error" and that "TE-weighted error" is the same thing as "L2 error". Those statements would both be incorrect. "Tenney-weighted error" is the "T1 error" and "TE-weighted error" is the "T2 error". I see that as of Jan '22, Flora has fixed this by removing the parenthesis, so that it's clear that the L1 error is being Tenney-weighted (to become T1) and the L2 error is being Tenney-weighted (to become T2). My previous comment did not reflect this understanding, stating that Tenney height was the L1 norm (it's actually the T1 norm) and that TE height was the L2 norm (it's actually the T2 norm). Erlich's "damage" is the T1-weighted absolute value of error though, so it is closely related to T2-weighted absolute value of error.

* But "error" should not be replaced with "damage" as I'd suggested. Damage is a weighted abs val of error. So the article states things with respect to "error" correctly.

--Cmloegcmluin (talk) 23:53, 5 March 2022 (UTC)

"Frobenius" tuning

Frobenius tuning has nothing to do with the Frobenius norm. It's simply the unweighted Euclidean norm. I propose renaming it to simply that: "unweighted Euclidean tuning".

The article also says:

This leads to a different tuning, the Frobenius tuning, which is perfectly functional but has less theoretical justification than TE tuning.

What theoretical justifications? This is ironic since the next paragraph proceeds to list several theoretical advantages of this tuning.

Not weighting the primes leads to -on average- errors that are the same across primes. It is the Tenney-Euclidean tuning that is biased towards lower primes and not the opposite. This is not a problem at all but the article is in no way clear on this. (In fact, even unweighted norms usually result in temperaments with a slight bias towards low primes, simply because the way temperaments are usually constructed (e.g. stacking edo maps) already has this bias (and especially wrt octaves))

-Sintel (talk) 19:37, 18 December 2021 (UTC)

I'm not sure if the name Frobenius tuning is derived from Frobenius norm.

The next part may be explained more clearly, but I'd like to remind you "the same error across primes" itself is a bias towards higher primes. Notice if 2 and 7 are equally weighted, 8 would get about thrice the error of 7's (see Graham's primerr.pdf). And no, I haven't observed the bias towards lower primes due to the way temperaments are constructed. FloraC (talk) 01:06, 19 December 2021 (UTC)

I've read Breed's paper and I think its very good work. Let me be clear: I think giving more weight to lower primes is a very good idea. But it seems obvious that this is explicitly introducing a certain bias to get better results in practice.

8 is not a prime, so when talking about average errors for the primes it is kind of irrelevant. In the case where you work in some subgroup like 2.5.9, I don't see why you would tolerate twice the error in 9 as you do for 3 in 2.3.5, as we are treating 9 here as a 'formal prime' and not even considering 3. Reading Breed's arguments further he does actually imply that his weighting is biased towards lower primes, but that this is a good thing.

I realize that this is just arguing semantics so I will not lose any sleep over it.

- Sintel (talk) 02:23, 19 December 2021 (UTC)

Here's where Gene defined Frobenius. He doesn't clarify his exact meaning though:

https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_12836.html#12836

I agree that the Frobenius norm is the wrong choice here. It's a matrix norm which treats a matrix like a vector, flattening it so to speak row-by-row into one single long row, and then doing essentially the L2/Euclidean norm on that. Why not just say Euclidean, then, since we're doing it on vectors.

I can see here:

https://yahootuninggroupsultimatebackup.github.io/tuning-math/topicId_12834#12841

That Gene is talking about using it on matrices. Perhaps in earlier times they were doing it to mappings rather than to tuning maps? Dunno.

So I've realized that I have another related terminological bone to pick here.

So I think it's okay to call it "Tenney-Euclidean error", or "TE error" for short.

And I think it's okay to call it "Tenney-Euclidean tuning", or "TE tuning" for short.

(A tuning is the tuning which minimizes the corresponding error, so from this point on, I'll just write error/tuning.)

But here's my concern. I think it's not okay to call it "Tenney-Euclidean-weighted error/tuning", or "TE-weighted error/tuning" for short.

Here's the reason: the "Euclidean" part of these name is not about weighting. It is about the minimized norm.

Errors/tunings have two separate defining characteristics: their weighting, and their minimized norm. The weighting applies to the primes error map. The minimized norm applies to the intervals and is different for each one. Here's a quick pic:

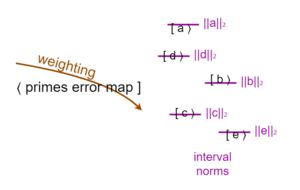
Yes, there is a norm which is minimized over the primes error map, and it is the dual norm to the norm minimized over the intervals, but it's the norm minimized over the intervals which is the one that defines the error/tuning (in the case of L2, which is self-dual, the norm is the same for the primes error map and the intervals, but for L1 tuning and L∞ tuning it's flipped).

Both defining characteristics have 3 possible values. So in total we have 3×3 of these types of errors/tunings. For weighting we have unweighted, (Tenney-)weighted, and Partch-weighted (inverse Tenney weighted). For norms we have L1 (Minkowskian), L2 (Euclidean), and L∞ (Chebyshevian). But not all of these types are popular. Almost no one uses Partch-weighting. Almost no one uses Chebyshevian norm minimization.

		norm
		L1 (Minkowskian)	L2 (Euclidean)	L∞ (Chebyshevian)
weight	unweighted		"Frobenius"
	(Tenney-)weighted	TIPTOP	TOP-RMS, TE
	Partch (inverse Tenney)

I'm just getting those names Minkowski and Chebyshev because they're associated with L1/taxicab/Manhattan distance and L∞/king/chessboard distance, respectively.

Unweighted is the default weighting (assume it if not specified). L1 is the default norm (assume it if not specified).

For whatever reason, historically, we've simply used Tenney's surname without adjectivizing it, but Euclid's surname with adjectivizing it. Perhaps this is simply an artifact of the weighting part of the name coming first, though it's clearly the case that sometimes it also comes at the end of the name, so it's hardly a complete explanation. In any case, I don't see a major problem with proceeding with this pattern.

So we can name errors/tunings in this format:

([weight eponym](-weighted)(-)([norm eponym adjective](-normed))

And if you use the word "weighted" or "normed" explicitly and the other term is present, you should use "weighted" or "normed" explicitly for that term too (edit: I recognize that this bit is way less important and more of a stylistic suggestion).

I'll give some examples.

These are all the same.

- Euclidean tuning

- Euclidean-normed tuning

- unweighted-Euclidean-normed tuning

(Since there's no eponym in the case of unweighted, I agree with Sintel that "unweighted Euclidean tuning" is an acceptable replacement name for "Frobenius tuning". I personally would just call it "Euclidean tuning", though.)

These are all the same.

- okay names:

- - Tenney tuning

- - Tenney-weighted tuning

- - Tenney-weighted-Minkowskian-normed tuning

- not okay names: okay, but stylistically concerning names: (edit: per Flora's thoughts, these names are fine. My concerns are merely stylistic)

- - Tenney-weighted-Minkowksian tuning

- - Tenney-Minkowskian-normed tuning

These are all the same.

- okay names:

- - Tenney-Euclidean tuning

- - Tenney-weighted-Euclidean-normed tuning

- - Tenney-Euclidean-normed tuning (edit: as per later comment, "Tenney" can be used unbound from weight, as an adjective for divide-by-log-of-prime, so this one has been moved to the "okay" category)

- okay, but stylistically concerning names:

- - Tenney-weighted-Euclidean tuning (edit: per Flora's thoughts, this name is fine. My concerns are merely stylistic)

- not okay names:

- - Tenney-Euclidean-weighted tuning

- - Tenney-normed-Euclidean tuning

Sorry, I know that's a lot, but hopefully it might help things click for some people. I can say, that in my personal case, the name "TE-weighted" has been causing me months of flailing agony basically until I was finally able to put all these insights together at once to see what was off about it. But of course maybe I’ve still got something wrong, or there are other good ways to think about it that I don’t see yet. --Cmloegcmluin (talk) 06:33, 27 January 2022 (UTC)

More related thoughts:

We don’t weight intervals. We don’t weight errors. (edit: We don't weight interval errors.)

We weight primes, when optimizing. (edit: We weight optimization targets. For tunings that optimize a set of target intervals, such a tonality diamond, those targets are of course those intervals. For tunings that optimize across all intervals (in the given interval subspace), those targets are the primes.)

So when someone says “TE norm” okay that’s perfectly fine. But it’s not a TE-‘’weighted'’ interval just because it’s divided by that norm. That’s an abuse of the word “weight”. Weighting is about importance in an optimizer’s priorities, not about an increase or decrease of size of error or interval.

So I take back one thing I said just above: you ‘’could’’ call it “TE-normed error/tuning” I suppose. Because “Tenney” isn’t bound to weight in the same way that “Euclidean” is bound to norm. Tenney just means divide by log of prime. So in that context it is being used for norm, not a weight. —-Cmloegcmluin (talk) 08:14, 27 January 2022 (UTC)

Woa your table is really enlightening! I mostly agree with you. As I figured "Tenney" was the weighting method and "Euclidean" was the norm method, on that basis I'd be more lax about calling them. I think Tenney-weighted-Euclidean tuning and Tenney-Euclidean-normed tuning are ok. FloraC (talk) 12:26, 27 January 2022 (UTC)

Nice! I'm glad it was helpful. And thanks for making the requested change. (Nice work on the Tenney height article yesterday, too).

You're right about "Tenney-weighted-Euclidean tuning". I realized that my recommendation against that type of name was way less important, merely a stylistic concern, so I made changes in my previous post here accordingly.

And I've moved "Tenney-Euclidean-normed" up into the completely okay category. I suggested it myself in my previous post but just didn't update my first post yet. I realized I have another way to explain why that one's okay. If you look at the Tenney-Euclidean error as [math]\displaystyle{ (eW)(i/||i||) }[/math] then that's a primes error map [math]\displaystyle{ e }[/math] with Tenney-weighted primes per the [math]\displaystyle{ W }[/math], multiplied with [math]\displaystyle{ i/||i|| }[/math] which could also be written [math]\displaystyle{ î }[/math] "i-hat", being the "normalized vector" or "unit vector" for the interval, specifically using the Euclidean norm. But we can group things a slightly different way, too: [math]\displaystyle{ (e)(Wi/||i||) }[/math], in which case you've just got a plain old primes error map, but then the other thing you got is a Tenney-Euclidean normed interval, because the [math]\displaystyle{ W }[/math] ("Tenney") matrix just has a diagonal of [math]\displaystyle{ 1/log₂p }[/math], so it puts stuff in the denominator along with that [math]\displaystyle{ ||i|| }[/math], resulting in an interval essentially divided by its TE-height AKA TE-norm. So that's basically just a mathematical rendition of the fact I stated in the previous post that Tenney in our context simply means that [math]\displaystyle{ 1/log₂p }[/math] thing, and is not necessarily bound to weight. --Cmloegcmluin (talk) 16:32, 27 January 2022 (UTC)

I've made another slight modification to something I wrote above, in order to generalize it to apply not only to all-interval optimization tunings like TE and TIPTOP, but also to target tunings. --Cmloegcmluin (talk) 22:24, 27 January 2022 (UTC)

I've been studying these tuning techniques a lot recently and think I may end up wanting to revise some of my statements above. Some of them may be just straight up wrong. Sorry for any confusion in the meantime, but I'll share my conclusions as soon as I can, when they're ready for prime time. Ha. Get it, "prime time". --Cmloegcmluin (talk) 00:53, 23 February 2022 (UTC)