|
|
| Line 1: |
Line 1: |
| <h2>IMPORTED REVISION FROM WIKISPACES</h2>
| | The ''32 equal division'' divides the [[Octave|octave]] into 32 equal parts of precisely 37.5 [[cent|cent]]s each. While even advocates of less-common [[EDO|edo]]s can struggle to find something about it worth noting, it does provide an excellent tuning for [[Petr_Parízek|Petr Parízek]]'s sixix temperament, which tempers out the [[5-limit|5-limit]] sixix comma, 3125/2916, using its 9\32 generator of size 337.5 cents. Parízek's preferred generator for sixix is (128/15)^(1/11), which is 337.430 cents and which gives equal error to fifths and major thirds, so 32edo does sixix about as well as sixix can be done. It also can be used (with the 9\32 generator) to tune mohavila, an 11-limit temperament which does not temper out sixix. |
| This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
| |
| : This revision was by author [[User:genewardsmith|genewardsmith]] and made on <tt>2012-11-15 14:58:14 UTC</tt>.<br>
| |
| : The original revision id was <tt>382978958</tt>.<br>
| |
| : The revision comment was: <tt></tt><br>
| |
| The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
| |
| <h4>Original Wikitext content:</h4>
| |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html">The //32 equal division// divides the [[octave]] into 32 equal parts of precisely 37.5 [[cent]]s each. While even advocates of less-common [[edo]]s can struggle to find something about it worth noting, it does provide an excellent tuning for [[Petr Parízek]]'s sixix temperament, which tempers out the [[5-limit]] sixix comma, 3125/2916, using its 9\32 generator of size 337.5 cents. Parízek's preferred generator for sixix is (128/15)^(1/11), which is 337.430 cents and which gives equal error to fifths and major thirds, so 32edo does sixix about as well as sixix can be done. It also can be used (with the 9\32 generator) to tune mohavila, an 11-limit temperament which does not temper out sixix.
| |
| [[media type="custom" key="18971266"]]
| |
| It also tempers out 2048/2025 in the 5-limit, and [[50_49|50/49]] with [[64_63|64/63]] in the [[7-limit]], which means it supports [[Diaschismic family|pajara temperament]], with a very sharp fifth of 712.5 cents which could be experimented with by those with a penchant for fifths even sharper than the fifth of [[27edo]]; this fifth is in fact very close to the minimax tuning of the pajara extension [[Diaschismic family#Pajara-Pajaro|pajaro]], using the 32f val. In the 11-limit it provides the optimal patent val for the 15&32 temperament, tempering out 55/54, 64/63 and 245/242.
| |
|
| |
|
| =Z function= | | It also tempers out 2048/2025 in the 5-limit, and [[50/49|50/49]] with [[64/63|64/63]] in the [[7-limit|7-limit]], which means it supports [[Diaschismic_family|pajara temperament]], with a very sharp fifth of 712.5 cents which could be experimented with by those with a penchant for fifths even sharper than the fifth of [[27edo|27edo]]; this fifth is in fact very close to the minimax tuning of the pajara extension [[Diaschismic_family#Pajara-Pajaro|pajaro]], using the 32f val. In the 11-limit it provides the optimal patent val for the 15&32 temperament, tempering out 55/54, 64/63 and 245/242. |
| | |
| | =Z function= |
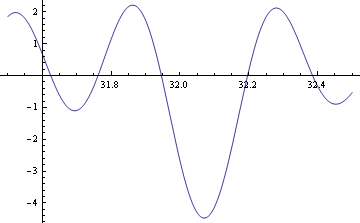
| Below is a plot of the Z function, showing how its peak (ie most negative) value is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third. | | Below is a plot of the Z function, showing how its peak (ie most negative) value is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third. |
|
| |
|
| [[image:plot32.png]] | | [[File:plot32.png|alt=plot32.png|plot32.png]] |
| | |
| | =Music= |
| | [http://micro.soonlabel.com/petr_parizek/3125_2916_temp_q32.ogg Sixix] by Petr Parízek |
|
| |
|
| =Music=
| | [http://micro.soonlabel.com/32edo/32-32-32-nothing-less-will-do.mp3 32 32 32 Nothing Less Will Do] by [[Chris_Vaisvil|Chris Vaisvil]] [[Category:edo]] |
| [[http://micro.soonlabel.com/petr_parizek/3125_2916_temp_q32.ogg|Sixix]] by Petr Parízek
| | [[Category:listen]] |
| [[http://micro.soonlabel.com/32edo/32-32-32-nothing-less-will-do.mp3|32 32 32 Nothing Less Will Do]] by [[@Chris Vaisvil]]</pre></div>
| | [[Category:sixix]] |
| <h4>Original HTML content:</h4>
| | [[Category:z]] |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html"><html><head><title>32edo</title></head><body>The <em>32 equal division</em> divides the <a class="wiki_link" href="/octave">octave</a> into 32 equal parts of precisely 37.5 <a class="wiki_link" href="/cent">cent</a>s each. While even advocates of less-common <a class="wiki_link" href="/edo">edo</a>s can struggle to find something about it worth noting, it does provide an excellent tuning for <a class="wiki_link" href="/Petr%20Par%C3%ADzek">Petr Parízek</a>'s sixix temperament, which tempers out the <a class="wiki_link" href="/5-limit">5-limit</a> sixix comma, 3125/2916, using its 9\32 generator of size 337.5 cents. Parízek's preferred generator for sixix is (128/15)^(1/11), which is 337.430 cents and which gives equal error to fifths and major thirds, so 32edo does sixix about as well as sixix can be done. It also can be used (with the 9\32 generator) to tune mohavila, an 11-limit temperament which does not temper out sixix.<br />
| |
| <!-- ws:start:WikiTextMediaRule:0:&lt;img src=&quot;http://www.wikispaces.com/site/embedthumbnail/custom/18971266?h=0&amp;w=0&quot; class=&quot;WikiMedia WikiMediaCustom&quot; id=&quot;wikitext@@media@@type=&amp;quot;custom&amp;quot; key=&amp;quot;18971266&amp;quot;&quot; title=&quot;Custom Media&quot;/&gt; --><script type="text/javascript" src="http://webplayer.yahooapis.com/player.js">
| |
| </script><!-- ws:end:WikiTextMediaRule:0 --><br />
| |
| It also tempers out 2048/2025 in the 5-limit, and <a class="wiki_link" href="/50_49">50/49</a> with <a class="wiki_link" href="/64_63">64/63</a> in the <a class="wiki_link" href="/7-limit">7-limit</a>, which means it supports <a class="wiki_link" href="/Diaschismic%20family">pajara temperament</a>, with a very sharp fifth of 712.5 cents which could be experimented with by those with a penchant for fifths even sharper than the fifth of <a class="wiki_link" href="/27edo">27edo</a>; this fifth is in fact very close to the minimax tuning of the pajara extension <a class="wiki_link" href="/Diaschismic%20family#Pajara-Pajaro">pajaro</a>, using the 32f val. In the 11-limit it provides the optimal patent val for the 15&amp;32 temperament, tempering out 55/54, 64/63 and 245/242.<br />
| |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:1:&lt;h1&gt; --><h1 id="toc0"><a name="Z function"></a><!-- ws:end:WikiTextHeadingRule:1 -->Z function</h1>
| |
| Below is a plot of the Z function, showing how its peak (ie most negative) value is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.<br />
| |
| <br />
| |
| <!-- ws:start:WikiTextLocalImageRule:5:&lt;img src=&quot;/file/view/plot32.png/219952208/plot32.png&quot; alt=&quot;&quot; title=&quot;&quot; /&gt; --><img src="/file/view/plot32.png/219952208/plot32.png" alt="plot32.png" title="plot32.png" /><!-- ws:end:WikiTextLocalImageRule:5 --><br />
| |
| <br />
| |
| <!-- ws:start:WikiTextHeadingRule:3:&lt;h1&gt; --><h1 id="toc1"><a name="Music"></a><!-- ws:end:WikiTextHeadingRule:3 -->Music</h1>
| |
| <a class="wiki_link_ext" href="http://micro.soonlabel.com/petr_parizek/3125_2916_temp_q32.ogg" rel="nofollow">Sixix</a> by Petr Parízek<br />
| |
| <a class="wiki_link_ext" href="http://micro.soonlabel.com/32edo/32-32-32-nothing-less-will-do.mp3" rel="nofollow">32 32 32 Nothing Less Will Do</a> by <a class="wiki_link" href="/Chris%20Vaisvil" target="_blank">Chris Vaisvil</a></body></html></pre></div>
| |
The 32 equal division divides the octave into 32 equal parts of precisely 37.5 cents each. While even advocates of less-common edos can struggle to find something about it worth noting, it does provide an excellent tuning for Petr Parízek's sixix temperament, which tempers out the 5-limit sixix comma, 3125/2916, using its 9\32 generator of size 337.5 cents. Parízek's preferred generator for sixix is (128/15)^(1/11), which is 337.430 cents and which gives equal error to fifths and major thirds, so 32edo does sixix about as well as sixix can be done. It also can be used (with the 9\32 generator) to tune mohavila, an 11-limit temperament which does not temper out sixix.
It also tempers out 2048/2025 in the 5-limit, and 50/49 with 64/63 in the 7-limit, which means it supports pajara temperament, with a very sharp fifth of 712.5 cents which could be experimented with by those with a penchant for fifths even sharper than the fifth of 27edo; this fifth is in fact very close to the minimax tuning of the pajara extension pajaro, using the 32f val. In the 11-limit it provides the optimal patent val for the 15&32 temperament, tempering out 55/54, 64/63 and 245/242.
Z function
Below is a plot of the Z function, showing how its peak (ie most negative) value is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.
Music
Sixix by Petr Parízek
32 32 32 Nothing Less Will Do by Chris Vaisvil
