Kite Guitar

The Kite Guitar

The Kite guitar (or bass, mandolin, banjo, etc.) uses 41 divisions of the octave instead of 12. 41-tET approximates 7-limit just intonation to within 3-6¢, and chords sound gorgeous! But a guitar with 41 frets per octave is impractical. The Kite guitar cleverly omits every other fret. Thus while the frets are closer together than a standard guitar, they're not so close as to be unplayable. The interval between open strings is 13 steps of 41. 13 is an odd number, thus all 41 pitches are present on the guitar. Each string has only half of the pitches, but any adjacent pair of strings has all 41.

Omitting half the frets in effect moves certain pitches to remote areas of the fretboard, and makes certain intervals difficult to play. Miraculously, it works out that the remote intervals are the ones that don't work well in chords, and the ones that aren't remote are the ones that do work well. For example, the sweet 5-limit major 3rd, a 5/4 ratio, is easily accessible, but the dissonant 3-limit major 3rd 81/64 isn't. (3-limit & 5-limit refer to the largest prime number in the frequency ratio.)

In addition, important 7-limit intervals like 7/6, 7/5 and 7/4 are easy to play. This means the Kite guitar can do much more than just play sweet Renaissance music. It can put a whole new spin on jazz, blues and experimental music. The dom7 and dom9 chords are especially calm and relaxed, revealing just how poorly 12-tET tunes these chords. But dissonance is still possible, in fact 41-tET can be far more dissonant than 12-tET. And 41 notes means that the melodic and harmonic vocabulary is greatly expanded, allowing truly unique music that simply isn't possible with 12 notes.

The Kite guitar has almost twice as many frets as a standard guitar. Even with these additional frets, the Kite guitar is still quite playable. The interval between open strings is usually a major 3rd, not a 4th. Thus new chord shapes must be learned. However, the Kite guitar is isomorphic, meaning that chord shapes can be moved not only from fret to fret but also from string to string. Thus there are far fewer shapes to learn. (Open tunings, which are non-isomorphic, are also possible.) Tuning in 3rds not 4ths reduces the overall range of the guitar. Thus a 7-string or even an 8-string guitar is desirable.

For more info: http://tallkite.com/misc_files/The%20Kite%20Tuning.pdf

Photographs

An 8-string electric guitar

Five early prototypes made with cable-tie frets

Recordings and Videos

A simple 12-bar blues by Aaron Wolf:

• https://soundcloud.com/mbirakite/aaron-wolf-12-bar-blues-on-kite-guitar

Open-tuning recordings by Sacred Skeleton aka Igliashon Jones:

• https://soundcloud.com/sacred-skeleton/modified-kite-guitar-take-1 (clean)
• https://soundcloud.com/sacred-skeleton/modified-kite-guitar-take-2 (fuzz)

Open tunings become more playable with the use of a "half-fret capo". From the liner notes:

"A couple of improvisations on a guitar loaned to me by Kite Giedratis. The guitar is fretted to 41 notes per double-octave, i.e. every other note of 41 notes per octave, using movable cable ties. On these tracks I modified the fretting slightly by moving the 2nd fret down one step of 41edo and then put a capo behind it, effectively moving all the frets above it UP by one step of 41edo, so that the frets all give odd-numbered pitches from 41edo instead of even-numbered ones. This gives frets for approximations to the ratios 21/20, 12/11, 9/8, 7/6, 6/5, 5/4, 9/7, 4/3, 11/8, and 10/7 relative to the open strings, which makes it possible to let the open strings ring out against pitches fretted low on the neck when the open strings are tuned to DADGAD or DGDGAD, my two favorite open tunings.

Without the offset I introduced, the normal fretting on Kite's guitar would have the lowest frets approximating 28/27, 16/15, 10/9, 8/7, 32/27, 11/9, 81/64, 15/11, 7/5, and 16/11, which doesn't work well for the open tunings I like but is rather designed to have the open strings tuned in parallel 3rds (5/4 or 6/5), for an isomorphic layout that facilitates chords built by stacking 3rds. I found that tuning somewhat challenging, being so unlike any open string tunings I've ever used before, and most of the intervals between non-adjacent open strings are rather discordant. Other players, whose styles don't lean as heavily on open strings and drones the way I do, may find Kite's original design preferable to my modification.

But anyway, the two designs can coexist on the same fretboard by simply inserting an extra fret between the 1st and 2nd instead of moving the 2nd fret lower as I have done, and by varying the tuning of the open strings as you please. It's a fantastic way to access the resources of 41edo on a guitar, without having an absurd number of very closely-spaced frets!"

Chords (major tuning)

There are many chords to explore, but the obvious place to start is with those of intervallic odd-limit 9 or less. These chords are mostly subsets of the 4:5:6:7:9 pentad or the 9/(9:7:6:5:4) pentad. Thus most of these chords can be classified as either harmonic or subharmonic. The only exceptions are the ^m7 and vm7 chords (and their homonyms v6 and ^6), which are classified as stacked chords, because they are formed by stacking complimentary 3rds. (Some chords fall outside these 3 categories.)

These tables list all the 9-odd-limit chords, plus the vM7 tetrad, which is odd limit 15 and stacked. The chord shapes are written in tablature, using fret numbers. The root is placed arbitrarily on the 4th fret. In these tables, the interval between open strings is always a downmajor 3rd. This makes the Kite guitar isomorphic, thus a tab like 4 6 3 5 can start on the 6th, 5th or 4th string. A skipped string is indicated by a period. Alternate fingerings are possible, especially for 2-finger and 3-finger chords.

Triads

Other voicings are possible; these are just the most convenient ones. The alternate names for the voicings are explained in the next section. The upmajor chord is a particularly dissonant triad.

chord type	sus4	up or upmajor	down or downmajor	upminor	downminor	sus2	updim	downdim
example, with homonym	C4 = F2	C^	Cv	C^m	Cvm	C2 = G4	C^dim	Cvdim
ratio of the 3rd	P4 = 4/3	^M3 = 9/7	vM3 = 5/4	^m3 = 6/5	vm3 = 7/6	M2 = 9/8	^m3 = 6/5	vm3 = 7/6
ratio of the 5th	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2	d5 = 7/5	d5 = 7/5
close voicing R 3 5 8
frets	4 6 3 5	4 5 3 5	4 4 3 5	4 3 3 5	4 2 3 5	4 1 3 5	4 3 1 5	4 2 1 5
suggested fingerings	2 4 1 3	2 3 1 4	2 3 1 4 2 2 1 4	2 1 1 3	3 1 2 4	3 1 2 4	3 2 1 4	3 2 1 4
open or high-3 voicing R 5 8 10
frets	4 . 3 5 7	4 . 3 5 6	4 . 3 5 5	4 . 3 5 4	4 . 3 5 3	4 . 3 5 2	4 . 1 5 4	4 . 1 5 3
suggested fingerings	2 . 1 3 4	2 . 1 3 4	2 . 1 3 4 2 . 1 4 4	2 . 1 4 3	3 . 1 4 2	3 . 2 4 1	2 . 1 4 3	3 . 1 4 2
1st inversion or high-1 voicing 3 5 8
frets	5 2 4	4 2 4	3 2 4	2 2 4	1 2 4	0 2 4	2 0 4	1 0 4
suggested fingerings	4 1 3	2 1 3	2 1 3	1 1 3	1 2 4	1 2 4	2 1 4	2 1 4
2nd inversion or low-5 voicing 5 R 3 5
frets	2 4 6 3	2 4 5 3	2 4 4 3	2 4 3 3	2 4 2 3	2 4 1 3	(difficult)	(difficult)
suggested fingerings	1 3 4 2	1 3 4 2	1 3 4 2	1 4 2 3 1 3 2 2	1 3 1 2	2 4 1 3

Seventh chords

It's generally impossible to voice 7th chords in 1st, 2nd or 3rd inversion close voicings, because the 7th occurs on the same string as the 8ve. Instead voicings are named as close (root position, R 3 5 7), high-3 (3rd raised an 8ve) and low-5 (5th lowered an 8ve). A high-3 low-5 voicing is possible (5 R 7 3). With 7 strings, a high-3-7 voicing is possible (R 5 3 7).

Adding a major 9th (ratio 9/4) to any of the first 4 tetrads sounds good. The up-7 chord is arguably improved by adding a 9th. 9ths are shown in parentheses. The no3, no5 and no7 (i.e. add9) versions of the ^9 and v9 chords are all 9-odd-limit chords.

chord type	downmajor-7 (downmajor-9)	up-7 (up-9)	down-7 (down-9)	upminor-7 (upminor-9)	downminor-7	up-halfdim	down-halfdim
example, with homonym	CvM7 (CvM9)	C^7 (C^9)	Cv7 (Cv9)	C^m7 = ^Ebv6 (C^m9 = ^EbvM7/C)	Cvm7 = vEb^6	C^m7(b5) = ^Ebvm6	Cvm7(b5) = vEb^m6
ratio of the 3rd	vM3 = 5/4	^M3 = 9/7	vM3 = 5/4	^m3 = 6/5	vm3 = 7/6	^m3 = 6/5	vm3 = 7/6
ratio of the 5th	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2	d5 = 7/5	d5 = 7/5
ratio of the 7th	vM7 =15/8	^m7 = 9/5	vm7 = 7/4	^m7 = 9/5	vm7 = 7/4	^m7 = 9/5	vm7 = 7/4
close voicing R 3 5 7 (9)
frets	4 4 3 3 (2)	4 5 3 2 (2)	4 4 3 1 (2)	4 3 3 2 (2)	4 2 3 1	4 3 1 2	4 2 1 1
suggested fingerings	3 4 2 2 (1) 3 3 2 2 (1) 1 1 1 1 (1)	3 4 2 1 (1)	3 4 2 1 4 4 3 1 (2)	4 2 3 1 (1) 3 2 2 1 (1)	4 2 3 1	4 3 1 2	4 2 1 1
high-3 voicing R 5 7 10
frets	4 . 3 3 5	4 . 3 2 6	4 . 3 1 5	4 . 3 2 4	4 . 3 1 3	4 . 1 2 4	4 . 1 1 3
suggested fingerings	2 . 1 1 3	3 . 2 1 4	3 . 2 1 4	3 . 2 1 4 2 . 1 1 4	4 . 2 1 3	3 . 1 2 4	4 . 1 1 3
low-5 voicing 5 R 3 7 (9)
frets	2 4 4 . 3 (2)	2 4 5 . 2 (2)	2 4 4 . 1	2 4 3 . 2 (2)	2 4 2 . 1	(difficult)	(difficult)
suggested fingerings	1 3 4 . 2 (1)	1 3 4 . 2 (2) 1 3 4 . 1 (1)	2 3 4 . 1	1 . 4 3 2 (2) 1 . 4 3 1 (1)	2 4 2 . 1

Sixth chords

Sixth chords are hard to voice. A close voicing in root position is generally impossible, because the 6th occurs on the same string as the 5th. One solution is to play a riff that alternates between the 5th and the 6th. Another is to omit the 5th, but then the chord can be mistaken for a triad in 1st inversion. Another voicing is the low-6 aka 3rd inversion (6 R 3 5). But this is the same as the close voicing of the corresponding 7th chord, and again the chord can be mistaken. A good non-ambiguous voicing is low-5 (5 R 3 6), but it can be a difficult stretch. Also the 9th from the 5th to the 6th is usually not a plain 9th, and can be dissonant. Other possibilities are high-3-5 (R 6 3 5), high-3-6 (R 5 3 6), high-5 (R 3 6 8 5) and high-6 (R 3 5 8 6).

The up-6 chord is particularly dissonant, unless voiced as its homonym the vm7 chord.

Adding a major 9th to any of these chords will make a wolf 4th with the 6th. Adding an 11th to either the ^m6 or the vm6 chord won't increase the odd limit above 9.

chord type	up-6 or upmajor-6	down-6 or downmajor-6	upminor-6	downminor-6
example, with homonym	C^6 = ^Avm7	Cv6 = vA^m7	C^m6 = ^Avm7(b5)	Cvm6 = vA^m7(b5)
ratio of the 3rd	^M3 = 9/7	vM3 = 5/4	^m3 = 6/5	vm3 = 7/6
ratio of the 5th	P5 = 3/2	P5 = 3/2	P5 = 3/2	P5 = 3/2
ratio of the 6th	^M6 = 12/7	vM6 = 5/3	^M6 = 12/7	vM6 = 5/3
close voicing for riffing R 3 5/6
frets	4 5 3/7	4 4 3/6	4 3 3/7	4 2 3/6
suggested fingerings	2 3 1/4	2 3 1/4	2 1 1/4	3 1 2/4
close no-5th voicing R 3 6	C^6no5 = ^Avm	Cv6no5 = vA^m	C^m6no5 = ^Avdim	Cvm6no5 = vA^dim
frets	4 5 7	4 4 6	4 3 7	4 2 6
suggested fingerings	1 2 4	1 1 3	2 1 4	2 1 4
low-6 voicing 6 R 3 5
frets	6 4 5 3	5 4 4 3	6 4 3 3	5 4 2 3
suggested fingerings	4 2 3 1	4 2 3 1	4 2 1 1	4 3 1 2
low-5 voicing 5 R 3 6
frets	2 4 5 7	2 4 4 6	2 4 3 7	2 4 2 6
suggested fingerings	1 2 3 4	1 2 3 4	1 3 2 4	1 3 1 4

11th chords include the vM9,v#11 (4 4 3 3 2 2), vM11 (4 4 3 3 2 0), v11 (4 4 3 1 2 0), and ^m11 (4 3 3 2 2 1). All but the first of these contain a wolf 11th. Rather than 8/3, the vM11 and v11 chords have 21/8, and the ^m11 chord has 27/10. The first chord's v#11th is 45/16, which is equivalent to 14/5, because 41edo tempers out the Ruyoyo comma. Thus the chord's odd limit is only 15.

Another chord with an innate Ruyoyo comma is vM7sus4 (4 6 3 3), in which the vM7 is both 15/8 and 28/15. Yet another is v7(b5) (4 4 2 2), in which the b5 is both 7/5 and 45/32.

Songs (major tuning)

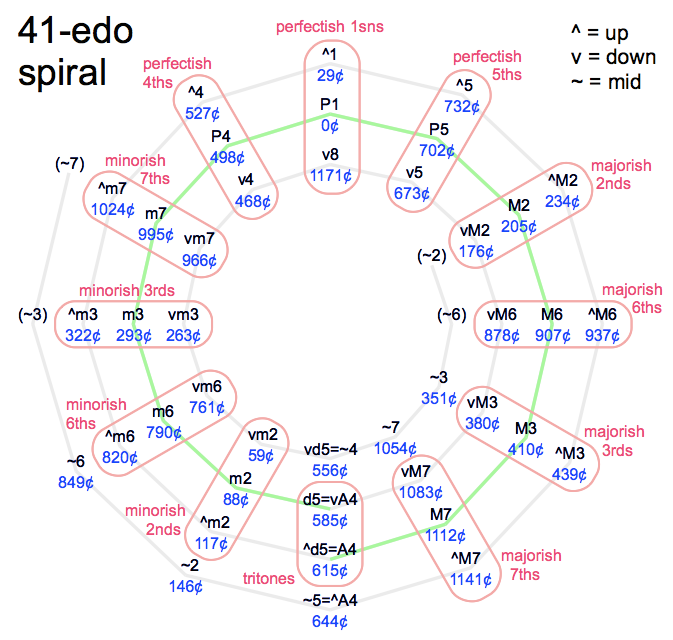
These conventional songs have been translated from 12edo to 41edo. One way to do this is to first translate it to 7-limit JI, perhaps visualizing it on a lattice, keeping in mind that 41-edo tempers out the Layo, Ruyoyo and Saruyo minicommas. Then translate the JI to 41edo. Another way is to use this chart which shows 41-edo in terms of 12-edo. The 12 categories circled in red correspond to the notes of 12-edo.

Often there is only one obvious way to translate a song. "La Bamba" is Iv - IVv - Vv7. Sometimes there are multiple obvious translations. For example, the first 3 chords of "When I Was Your Man" are II7 - IIm7 - I. That could become vII^7 - vII^m7 - Iv, or it could become ^IIv7 - ^IIvm7 - Iv.

In general, upperfect and downperfect intervals within chords are to be avoided. Downmajor is preferred over upmajor. Upminor is preferred for most folk, but downminor is preferred for most blues. Avoid plain major and minor 3rds and 6ths.

Comma pumps, other than the aforementioned minicommas, cause pitch shifts, or occasionally, a tonic drift. The two most common commas that cause issues are the Gu and Ru commas. The choice of which two chords in the pump contain the pitch shift can be tricky. Generally, a root movement by an ^4, v4, ^5 or v5 is avoided. This usually necessitates a root movement by a plain major or minor interval.

For example, the Gu pump might be I - VIm - IIm - V7 - I. Without the pump, I - VIm would be translated as Iv - vVI^m, to avoid shifts. The roots would move by a vM6. With the pump, this might translate to Iv - VI^m - II^m - Vv7 - Iv. The first root movement is by a M6. The tonic and the major 3rd both shift between the I chord and the VI chord. Sometimes an up- or down-perfect root movement is better, see "I Will" below.

Likewise, the Ru pump might be I7 - IV7 - V7 - I7. The usual translation is Iv7 - IVv7 - Vv7 - Iv7, with the 4th shifting between the IV and V chords. Another example is Im7 - bIIIm6 - bVII7 - IV7 - I7. The root movements are m3, P5, P5, P5. Without the pump, the m3 movement would be translated to vm3. With the pump, to avoid an ^5 movement, the translation is Iv7 - bIII^m6 - bVIIv7 - IVv7 - I.

One way to hide pitch shifts is to voice the two occurrences of the pitch in different octaves. Another way is to omit the 5th in one of the chords. Thus in the Gu example, the 2nd chord might be VI^mno5.

Actual song translations are on separate pages, grouped by translator. if you have any translations, feel free to add your own page!