Kite's color notation: Difference between revisions
added a section on converting color names to/from monzos |
No edit summary |
||
| Line 1: | Line 1: | ||
This is | This is a <u>very</u> brief summary. For a full explanation, see [[KiteGiedraitis|Kite's]] book, [http://www.tallkite.com/AlternativeTunings.html "Alternative Tunings: Theory, Notation and Practice"]. | ||
== Color Names for Primes 3, 5 and 7 == | == Color Names for Primes 3, 5 and 7 == | ||
Every prime above 3 has two colors, an '''over''' color (prime in the numerator) and an '''under''' color (prime in the denominator). Over colors end with -o, and under colors end with -u. The color for 3-limit ends in -a for '''all''', which includes over (3/2, 9/8), under (4/3, 16/9) and neither (1/1, 2/1). | Every prime above 3 has two colors, an '''over''' color (prime in the numerator) and an '''under''' color (prime in the denominator). Over colors end with -o, and under colors end with -u. The color for 3-limit ends in -a for '''all''', which includes over (3/2, 9/8), under (4/3, 16/9) and neither (1/1, 2/1). | ||
'''Wa''' = white (strong but colorless) = 3-limit | '''Wa''' = white (strong but colorless) = 3-limit <br/> | ||
'''Yo''' = yellow (warm and sunny) = 5-over = major <br/> | |||
'''Yo''' = yellow (warm and sunny) = 5-over = major | '''Gu''' ("goo") = green (not as bright as yellow) = 5-under = minor <br/> | ||
'''Zo''' = blue/azure (dark and bluesy) = 7-over = subminor <br/> | |||
'''Gu''' ("goo") = green (not as bright as yellow) = 5-under = minor | '''Ru''' = red (alarming, inflamed) = 7-under = supermajor | ||
'''Zo''' = blue/azure (dark and bluesy) = 7-over = subminor | |||
'''Ru''' = red (alarming, inflamed) = 7-under = supermajor | |||
The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Colors are abbreviated as w, y, z, etc. Use z (azure) not b (blue), because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom. | The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Colors are abbreviated as w, y, z, etc. Use z (azure) not b (blue), because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom. | ||
== Interval Names == | == Interval Names == | ||
| Line 27: | Line 21: | ||
21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g<sup>3</sup>2. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd. | 21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g<sup>3</sup>2. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd. | ||
The next table lists various 7-limit intervals, see the [[Gallery of Just Intervals]] for many more examples. | |||
{| class="wikitable" | |||
!'''ratio''' | |||
!'''cents''' | |||
!'''color & degree''' | |||
!'''shorthand''' | |||
|- | |||
|1/1 | |||
|0¢ | |||
|wa unison | |||
|w1 | |||
|- | |||
|21/20 | |||
|84¢ | |||
|zogu 2nd | |||
|zg2 | |||
|- | |||
|16/15 | |||
|112¢ | |||
|gu 2nd | |||
|g2 | |||
|- | |||
|10/9 | |||
|182¢ | |||
|yo 2nd | |||
|y2 | |||
|- | |||
|9/8 | |||
|204¢ | |||
|wa 2nd | |||
|w2 | |||
|- | |||
|8/7 | |||
|231¢ | |||
|ru 2nd | |||
|r2 | |||
|- | |||
|7/6 | |||
|267¢ | |||
|zo 3rd | |||
|z3 | |||
|- | |||
|32/27 | |||
|294¢ | |||
|wa 3rd | |||
|w3 | |||
|- | |||
|6/5 | |||
|316¢ | |||
|gu 3rd | |||
|g3 | |||
|- | |||
|5/4 | |||
|386¢ | |||
|yo 3rd | |||
|y3 | |||
|- | |||
|9/7 | |||
|435¢ | |||
|ru 3rd | |||
|r3 | |||
|- | |||
|21/16 | |||
|471¢ | |||
|zo 4th | |||
|z4 | |||
|- | |||
|4/3 | |||
|498¢ | |||
|wa 4th | |||
|w4 | |||
|- | |||
|27/20 | |||
|520¢ | |||
|gu 4th | |||
|g4 | |||
|- | |||
|7/5 | |||
|583¢ | |||
|zogu 5th | |||
|zg5 | |||
|- | |||
|45/32 | |||
|590¢ | |||
|yo 4th | |||
|y4 | |||
|- | |||
|64/45 | |||
|610¢ | |||
|gu 5th | |||
|g5 | |||
|- | |||
|10/7 | |||
|617¢ | |||
|ruyo 4th | |||
|ry4 | |||
|- | |||
|40/27 | |||
|680¢ | |||
|yo 5th | |||
|y5 | |||
|- | |||
|3/2 | |||
|702¢ | |||
|wa 5th | |||
|w5 | |||
|- | |||
|32/21 | |||
|729¢ | |||
|ru 5th | |||
|r5 | |||
|- | |||
|14/9 | |||
|765¢ | |||
|zo 6th | |||
|z6 | |||
|- | |||
|8/5 | |||
|814¢ | |||
|gu 6th | |||
|g6 | |||
|- | |||
|5/3 | |||
|884¢ | |||
|yo 6th | |||
|y6 | |||
|- | |||
|27/16 | |||
|906¢ | |||
|wa 6th | |||
|w6 | |||
|- | |||
|12/7 | |||
|933¢ | |||
|ru 6th | |||
|r6 | |||
|- | |||
|7/4 | |||
|969¢ | |||
|zo 7th | |||
|z7 | |||
|- | |||
|16/9 | |||
|996¢ | |||
|wa 7th | |||
|w7 | |||
|- | |||
|9/5 | |||
|1018¢ | |||
|gu 7th | |||
|g7 | |||
|- | |||
|15/8 | |||
|1088¢ | |||
|yo 7th | |||
|y7 | |||
|- | |||
|40/21 | |||
|1116¢ | |||
|ruyo 7th | |||
|ry7 | |||
|- | |||
|2/1 | |||
|1200¢ | |||
|wa octave | |||
|w8 | |||
|} | |||
Yo and ru intervals tend to be major, and gu and zo ones tend to be minor. But interval quality is redundant (if a third is yo, it must be major) and not unique (there are other major thirds available). See the "Higher Primes" section below for why quality isn't used with color names. Instead of augmented and diminished, remote intervals are '''large''' (fifthward) and '''small''' (fourthward), abbreviated L and s. '''Central''' means neither large nor small. The '''magnitude''' is found by adding up all the monzo exponents except the first one, dividing by 7, and rounding off. 0 = central, 1 = large, 2 = double large, etc. 81/64 = Lw3, 135/128 = Ly1. Magnitudes do not add up predictably like colors and degrees do: w2 + w2 = Lw3. | |||
[[File:Lattice41a.png|833x833px]] | [[File:Lattice41a.png|833x833px]] | ||
A '''comma''' is 10-50¢, a '''minicomma''' is 1-10¢, and a '''microcomma''' is 0-1¢. These categories allow us to omit the magnitude in the spoken name. Thus sgg2 is not the small gugu 2nd, but simply the gugu comma. The double-large wa negative 2nd (the pyth comma) is simply the wa comma. 81/80 = g1 is the gu comma. LLg-2 = g1 + LLw-2 is also gu and also a comma, but LLg-2 is not <u>the</u> gu comma, because its odd limit is higher. Thus its name can't be shortened. | A '''comma''' is 10-50¢, a '''minicomma''' is 1-10¢, and a '''microcomma''' is 0-1¢. These categories allow us to omit the magnitude in the spoken name. Thus sgg2 is not the small gugu 2nd, but simply the gugu comma. The double-large wa negative 2nd (the pyth comma) is simply the wa comma. 81/80 = g1 is the gu comma. LLg-2 = g1 + LLw-2 is also gu and also a comma, but LLg-2 is not <u>the</u> gu comma, because its odd limit is higher. Thus its name can't be shortened. | ||
== Note Names == | == Note Names == | ||
Notes are named | Notes are named zEb, yyG#, etc. spoken as "zo E flat", "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa. The relative-notation lattice above can be superimposed on this absolute-notation lattice to name every note. Thus D + y3 = yF#, and from yE to ryF# = r2. | ||
[[File:Lattice51.png|frameless|962x962px]] | [[File:Lattice51.png|frameless|962x962px]] | ||
| Line 44: | Line 203: | ||
Prime 2 (even more colorless than wa) is clear, abbreviated '''ca''', and yaza noca = 3.5.7. 2-limit intervals like 2/1 are called wa not clear, for simplicity. | Prime 2 (even more colorless than wa) is clear, abbreviated '''ca''', and yaza noca = 3.5.7. 2-limit intervals like 2/1 are called wa not clear, for simplicity. | ||
Subgroups which omit 5 or 7 are '''noya''' or '''noza''', and those which omit both are '''noyaza'''. Unlike nowa, these terms aren't used in actual subgroup names. They are general descriptive terms, e.g. zala, latha and zalatha are all noya. | |||
== Color Names for Higher Primes == | == Color Names for Higher Primes == | ||
Colors for primes greater than 7 are named after the number itself, using the prefix i- for disambiguation as needed: | Colors for primes greater than 7 are named after the number itself, using the prefix i- for disambiguation as needed: | ||
'''ilo''' = 11-over, '''lu''' = 11-under, and '''la''' = 11-all = 2.3.11 (ilo not lo, because "lo C" sounds like "low C"). ilo and lu are abbreviated to '''1o''' and '''1u''' on the score and in interval names and chord names, e.g. ilo A = 1oA, ilo 4th = 1o4 = 11/8 and C ilo-7 = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both ilo and lu, since they are only 7.1¢ apart. Lavender is a '''pseudocolor''' that implies the [http://x31eq.com/cgi-bin/rt.cgi?ets=24_17&limit=2_3_11 Neuter] temperament. ilo notes could be called lovender, and lu notes could be called luvender. Both are "shades" of lavender. | '''ilo''' ("ee-LOW") = 11-over, '''lu''' = 11-under, and '''la''' = 11-all = 2.3.11 (ilo not lo, because "lo C" sounds like "low C"). ilo and lu are abbreviated to '''1o''' and '''1u''' on the score and in interval names and chord names, e.g. ilo A = 1oA, ilo 4th = 1o4 = 11/8 and C ilo-7 = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both ilo and lu, since they are only 7.1¢ apart. Lavender is a '''pseudocolor''' that implies the [http://x31eq.com/cgi-bin/rt.cgi?ets=24_17&limit=2_3_11 Neuter] temperament. ilo notes could be called lovender, and lu notes could be called luvender. Both are "shades" of lavender. | ||
'''Tho''' = 13-over, '''thu''' = 13-under, and '''tha''' = 13-all. Tho and thu are abbreviated as '''3o''' and '''3u''' on the score and in interval names, e.g. 13/8 = 3o6 = tho 6th. Languages without a "th" sound might use '''tro''', '''tru''' and '''tra'''. See the appendix in [http://www.tallkite.com/AlternativeTunings.html Kite's book] for more on translating colors. | '''Tho''' = 13-over, '''thu''' = 13-under, and '''tha''' = 13-all. Tho and thu are abbreviated as '''3o''' and '''3u''' on the score and in interval names, e.g. 13/8 = 3o6 = tho 6th. Languages without a "th" sound might use '''tro''', '''tru''' and '''tra'''. See the appendix in [http://www.tallkite.com/AlternativeTunings.html Kite's book] for more on translating colors into other languages. | ||
Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13. and yazalatha = 2.3.5.7.11.13 = the full 13-limit. '''Noya''' is a general term, not used in actual subgroup names, that indicates the absence of 5 and the presence of higher primes, e.g. zala, latha and zalatha. | Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13. and yazalatha = 2.3.5.7.11.13 = the full 13-limit. '''Noya''' is a general term, not used in actual subgroup names, that indicates the absence of 5 and the presence of higher primes, e.g. zala, latha and zalatha. | ||
| Line 66: | Line 227: | ||
The disambiguation prefix i- is only needed when the color word appears alone, and confusion is possible. Thus 11/7 = loru 5th, not iloru 5th, and 29o = twenty-no, not twenty-ino. | The disambiguation prefix i- is only needed when the color word appears alone, and confusion is possible. Thus 11/7 = loru 5th, not iloru 5th, and 29o = twenty-no, not twenty-ino. | ||
== Converting a | == Converting a ratio to/from a color name == | ||
Converting a [[Monzos|monzo]] | Converting a ratio: Find the [[Monzos|monzo]] by prime factorization. To find the color, combine all the appropriate colors for each prime > 3, higher primes first. To find the degree, first find the stepspan, which is the dot product of the monzo with the 7edo [[Patent val|edomapping]] <7 11 16 20 24 26 29 30...|. Then add 1, or subtract 1 if the stepspan is negative. To find the magnitude, add up all the monzo exponents except the first one, divide by 7, and round off. Combine the magnitude, color and degree to make the color name. | ||
Example: ratio = 63/40, monzo = |-3 2 -1 1>, color = zg, stepspan = -21+22-16+20 = 5, degree = 5+1 = 6, magnitude = round [(2-1+1)/7] = round (2/7) = 0, interval = zg6. | |||
Converting a color name: Let S be the stepspan of the interval, S = degree - sign (degree). Let M be the magnitude of the color name, with L = 1, LL = 2, etc. Small is negative and central is zero. Let the monzo be |a b c d e...>. The colors directly give you all the monzo entries except a and b. Let X = the dot product of |0 0 c d e...> with the 7edo edomapping. Then b = (2S - 2X + 3) mod 7 + 7M - 3, and a = (S - X - 11b) / 7. Convert the monzo to a ratio. | |||
Example: interval = sgg2, S = 2-1 = 1, M = -1, monzo = |a b -2>, X = <7 11 16| dot |0 0 -2> = -32, b = (2-(-64)+3) mod 7 + 7(-1) - 3 = 6-7-3 = -4, a = (1-(-32)-(-44))/7 = 77/7 = 11, monzo = |11 -4 -1>, ratio = 2048/2025. | |||
== Chord Names == | == Chord Names == | ||
Revision as of 20:13, 24 October 2018
This is a very brief summary. For a full explanation, see Kite's book, "Alternative Tunings: Theory, Notation and Practice".
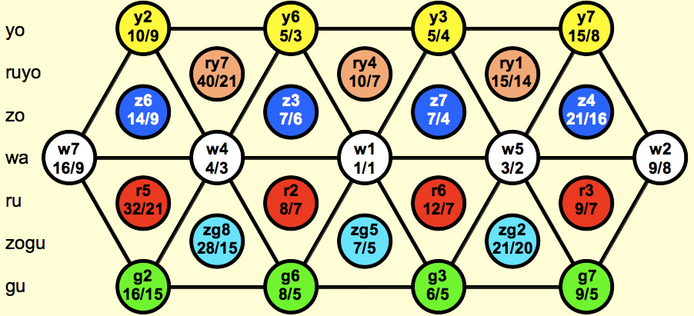
Color Names for Primes 3, 5 and 7
Every prime above 3 has two colors, an over color (prime in the numerator) and an under color (prime in the denominator). Over colors end with -o, and under colors end with -u. The color for 3-limit ends in -a for all, which includes over (3/2, 9/8), under (4/3, 16/9) and neither (1/1, 2/1).
Wa = white (strong but colorless) = 3-limit
Yo = yellow (warm and sunny) = 5-over = major
Gu ("goo") = green (not as bright as yellow) = 5-under = minor
Zo = blue/azure (dark and bluesy) = 7-over = subminor
Ru = red (alarming, inflamed) = 7-under = supermajor
The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Colors are abbreviated as w, y, z, etc. Use z (azure) not b (blue), because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom.
Interval Names
A color and a degree indicates a ratio, and vice versa. Every ratio has a spoken name and a written name. For 3/2, they are wa 5th and w5. Colors and degrees always add up predictably: z3 + g3 = zg5 = zogu 5th. Zogu not guzo, higher primes always come first. Opposite colors cancel: y3 + g3 = w5.
The JI lattice consists of many lattice rows, each one a chain of 5ths. Each lattice row has its own color, and each color has its own lattice row.
21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g32. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd.
The next table lists various 7-limit intervals, see the Gallery of Just Intervals for many more examples.
| ratio | cents | color & degree | shorthand |
|---|---|---|---|
| 1/1 | 0¢ | wa unison | w1 |
| 21/20 | 84¢ | zogu 2nd | zg2 |
| 16/15 | 112¢ | gu 2nd | g2 |
| 10/9 | 182¢ | yo 2nd | y2 |
| 9/8 | 204¢ | wa 2nd | w2 |
| 8/7 | 231¢ | ru 2nd | r2 |
| 7/6 | 267¢ | zo 3rd | z3 |
| 32/27 | 294¢ | wa 3rd | w3 |
| 6/5 | 316¢ | gu 3rd | g3 |
| 5/4 | 386¢ | yo 3rd | y3 |
| 9/7 | 435¢ | ru 3rd | r3 |
| 21/16 | 471¢ | zo 4th | z4 |
| 4/3 | 498¢ | wa 4th | w4 |
| 27/20 | 520¢ | gu 4th | g4 |
| 7/5 | 583¢ | zogu 5th | zg5 |
| 45/32 | 590¢ | yo 4th | y4 |
| 64/45 | 610¢ | gu 5th | g5 |
| 10/7 | 617¢ | ruyo 4th | ry4 |
| 40/27 | 680¢ | yo 5th | y5 |
| 3/2 | 702¢ | wa 5th | w5 |
| 32/21 | 729¢ | ru 5th | r5 |
| 14/9 | 765¢ | zo 6th | z6 |
| 8/5 | 814¢ | gu 6th | g6 |
| 5/3 | 884¢ | yo 6th | y6 |
| 27/16 | 906¢ | wa 6th | w6 |
| 12/7 | 933¢ | ru 6th | r6 |
| 7/4 | 969¢ | zo 7th | z7 |
| 16/9 | 996¢ | wa 7th | w7 |
| 9/5 | 1018¢ | gu 7th | g7 |
| 15/8 | 1088¢ | yo 7th | y7 |
| 40/21 | 1116¢ | ruyo 7th | ry7 |
| 2/1 | 1200¢ | wa octave | w8 |
Yo and ru intervals tend to be major, and gu and zo ones tend to be minor. But interval quality is redundant (if a third is yo, it must be major) and not unique (there are other major thirds available). See the "Higher Primes" section below for why quality isn't used with color names. Instead of augmented and diminished, remote intervals are large (fifthward) and small (fourthward), abbreviated L and s. Central means neither large nor small. The magnitude is found by adding up all the monzo exponents except the first one, dividing by 7, and rounding off. 0 = central, 1 = large, 2 = double large, etc. 81/64 = Lw3, 135/128 = Ly1. Magnitudes do not add up predictably like colors and degrees do: w2 + w2 = Lw3.
A comma is 10-50¢, a minicomma is 1-10¢, and a microcomma is 0-1¢. These categories allow us to omit the magnitude in the spoken name. Thus sgg2 is not the small gugu 2nd, but simply the gugu comma. The double-large wa negative 2nd (the pyth comma) is simply the wa comma. 81/80 = g1 is the gu comma. LLg-2 = g1 + LLw-2 is also gu and also a comma, but LLg-2 is not the gu comma, because its odd limit is higher. Thus its name can't be shortened.
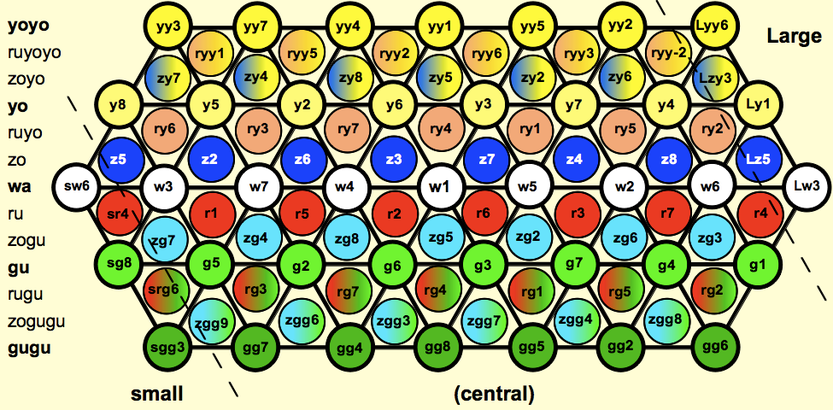
Note Names
Notes are named zEb, yyG#, etc. spoken as "zo E flat", "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa. The relative-notation lattice above can be superimposed on this absolute-notation lattice to name every note. Thus D + y3 = yF#, and from yE to ryF# = r2.
Prime Subgroup Names
Just as wa means 3-all or 3-limit, ya means 5-all and includes wa, yo, gu, yoyo, gugu, etc. Ya = the 2.3.5 prime subgroup = 5-limit. Za = 7-all = 2.3.7. Yaza = 2.3.5.7 = the full 7-limit. Nowa means without wa, and yaza nowa = 2.5.7.
Prime 2 (even more colorless than wa) is clear, abbreviated ca, and yaza noca = 3.5.7. 2-limit intervals like 2/1 are called wa not clear, for simplicity.
Subgroups which omit 5 or 7 are noya or noza, and those which omit both are noyaza. Unlike nowa, these terms aren't used in actual subgroup names. They are general descriptive terms, e.g. zala, latha and zalatha are all noya.
Color Names for Higher Primes
Colors for primes greater than 7 are named after the number itself, using the prefix i- for disambiguation as needed:
ilo ("ee-LOW") = 11-over, lu = 11-under, and la = 11-all = 2.3.11 (ilo not lo, because "lo C" sounds like "low C"). ilo and lu are abbreviated to 1o and 1u on the score and in interval names and chord names, e.g. ilo A = 1oA, ilo 4th = 1o4 = 11/8 and C ilo-7 = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both ilo and lu, since they are only 7.1¢ apart. Lavender is a pseudocolor that implies the Neuter temperament. ilo notes could be called lovender, and lu notes could be called luvender. Both are "shades" of lavender.
Tho = 13-over, thu = 13-under, and tha = 13-all. Tho and thu are abbreviated as 3o and 3u on the score and in interval names, e.g. 13/8 = 3o6 = tho 6th. Languages without a "th" sound might use tro, tru and tra. See the appendix in Kite's book for more on translating colors into other languages.
Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13. and yazalatha = 2.3.5.7.11.13 = the full 13-limit. Noya is a general term, not used in actual subgroup names, that indicates the absence of 5 and the presence of higher primes, e.g. zala, latha and zalatha.
On the score and in note names, the 1o accidental either raises by 33/32 or lowers by 729/704. The meaning will usually be clear from context, however it's safer to write at the top of the page either "1o4 = P4" or "1o4 = A4". Likewise, 3o6 should be noted as either m6 or M6. While the note 11/8 above C can be written two ways, either as 1oF or as 1oF#, the interval 11/8 can only be written one way, as 1o4. Likewise, 13/8 above C is either 3oA or 3oA♭, but 13/8 is only 3o6. This is the rationale for using large/small rather than major/minor. 11/9 is ambiguously major or minor, but unambiguously central. Intervals names and chord names become unambiguous for la and tha intervals. Also, commonly used intervals and chords are all central, and get concise names: gu 3rd not gu minor 3rd, A gu not A gu minor, etc. (see chord names below).
So = 17-over, su = 17-under, and sa = 17-all, abbreviated as 17o and 17u. Iso is an alternate form of so, to distinguish it from the solfege syllable Sol.
Ino = 19-over, nu = 19-under, and na = 19-all, abbreviated as 19o and 19u. Ino because "no 3rd" could mean either 19/16 or thirdless. Inu is an alternate form of nu, to distinguish "the nu key" from "the new key". 12edo implies yasana = 2.3.5.17.19.
Twenty-tho = 23-over, twenty-thu = 23-under, twenty-tha =23-all, abbreviated as 23o, 23u and 23a. 2.3.5.7.23 = yaza23a = "yaza-twenty-tha".
Similarly, twenty-no/-nu/-na = 29o/29u/29a, thirty-wo/-wu/-wa = 31o/31u/31a, thirty-so/-su/-sa = 37o/37u/37a, etc.
The disambiguation prefix i- is only needed when the color word appears alone, and confusion is possible. Thus 11/7 = loru 5th, not iloru 5th, and 29o = twenty-no, not twenty-ino.
Converting a ratio to/from a color name
Converting a ratio: Find the monzo by prime factorization. To find the color, combine all the appropriate colors for each prime > 3, higher primes first. To find the degree, first find the stepspan, which is the dot product of the monzo with the 7edo edomapping <7 11 16 20 24 26 29 30...|. Then add 1, or subtract 1 if the stepspan is negative. To find the magnitude, add up all the monzo exponents except the first one, divide by 7, and round off. Combine the magnitude, color and degree to make the color name.
Example: ratio = 63/40, monzo = |-3 2 -1 1>, color = zg, stepspan = -21+22-16+20 = 5, degree = 5+1 = 6, magnitude = round [(2-1+1)/7] = round (2/7) = 0, interval = zg6.
Converting a color name: Let S be the stepspan of the interval, S = degree - sign (degree). Let M be the magnitude of the color name, with L = 1, LL = 2, etc. Small is negative and central is zero. Let the monzo be |a b c d e...>. The colors directly give you all the monzo entries except a and b. Let X = the dot product of |0 0 c d e...> with the 7edo edomapping. Then b = (2S - 2X + 3) mod 7 + 7M - 3, and a = (S - X - 11b) / 7. Convert the monzo to a ratio.
Example: interval = sgg2, S = 2-1 = 1, M = -1, monzo = |a b -2>, X = <7 11 16| dot |0 0 -2> = -32, b = (2-(-64)+3) mod 7 + 7(-1) - 3 = 6-7-3 = -4, a = (1-(-32)-(-44))/7 = 77/7 = 11, monzo = |11 -4 -1>, ratio = 2048/2025.
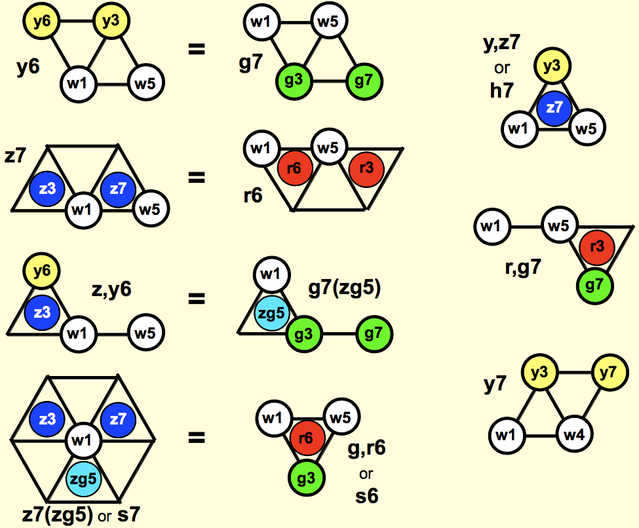
Chord Names
Triads are named after their 3rd, e.g. Cy. "Yo C" is a note, "C yo" is a chord. The four main yaza triads:
If the root isn't wa, the root color is added to the interval color: "yo A gu" = yAg = yA + (w1 g3 w5) = yA + wC + yE.
Tetrads are named Cy6 ("C yo six"), Dg7, etc. The 11 main yaza tetrads, with chord homonyms (same shape, different root) equated:
The y,z7 chord is also called the h7 chord ("aitch-seven"), because it's part of the harmonic series. The s7 ("sub-seven") chord is part of the subharmonic series. It's the first 7 subharmonics, with the 3rd subharmonic becoming the root. Note that s7 has no 7th. There are h9 chords, s11 chords, etc. The number must be odd, Ch8 is invalid. Ch9,13 = w1 y3 w5 z7 w9 3o13 has an added 13th harmonic.
A 9th chord contains a 3rd, 5th and 7th. An 11th chord contains all these plus a 9th. A 13th chord contains all these plus an 11th. The 5th, 9th and/or 13th default to wa. The 6th, 7th, and/or 11th default to the color of the 3rd. Thus Cy13 = w1 y3 w5 y7 w9 y11 w13, and Cy9 and Cy11 are subsets of this chord. However, an add-11 chord defaults to a wa 11: Cz7,11 = w1 z3 w5 z7 w11. Added 9ths default to wa: Cy,9 = w1 y3 w5 w9.
Alterations are always in parentheses, additions never are, e.g. z7(zg5). An alteration's degree must match a note in the chord, e.g. z7(y6) is invalid. But an exception is made for sus chords, where degree 2 or 4 alter the 3rd: C(z4) = w1 z4 w5. The sus note defaults to wa: Cy9(4) = w1 w4 w5 y7 w9.
Omissions are indicated by "no", the Hendrix chord might be Ch7z10no5. Enharmonic substitutions aren't allowed, 7/3 is a m10, not an A9. A no3 chord can also be written as a 5 chord with an added note: C5z7 = w1 w5 z7, and C(zg5)z7 = w1 zg5 z7. Omissions in harmonic and subharmonic chords refer to degree not harmonic. Ch11no3 omits y3, not the 3rd harmonic w5. However, numbers ≥ 15 always refer to (sub)harmonics, as in Ch15 or Cs15.
Staff notation
Notes on the staff default to wa. Non-wa notes have a color accidental like g, ry, etc. Like conventional sharp/flat accidentals, they apply to every such note in the measure and in the same octave. Unlike conventional accidentals which apply to a note (e.g. A), color accidentals only apply to one specific "version" of that note (e.g. A flat or A natural). For example, the yo accidental in the first chord applies to all the D naturals in that measure, but not to the D flats.
Staff notation can optionally include a color signature written above the staff. This makes color notation more similar to Johnston notation.
Color notation can optionally be made more similar to Sagittal notation by including two more accidentals, p and q (long forms po and qu = "ku"), to indicate raising/lowering by a pythagorean comma. For example, yF# = ypG♭, and zE♭= zqD#. This allows trills to always be written as a 2nd, less cluttered.
Chord Progressions, Keys and Modulations
The tonic is always wa. The root of each chord has a color, which defaults to wa. C - Am - F - G7 might be Cy - yAg - Fy - Gy,w7.
In relative notation, the I, IV and V chords default to a wa root. II, III, VI and VII must have an explicit root-color. gCy - gGy - Ag becomes gIIIy - gVIIy - Ig.
In adaptive JI, chords are just, but roots move by tempered intervals. Comma pumps are indicated with brackets: Cy - yAg - [y=w]Dg - Gy - Cy.
Keys are named after the colors used. The B♭h7 - E♭h7 - B♭h7 - Fh9 example above is in B♭ yo zo. Analogous to the relative and parallel major or minor, one can modulate to relative gu, parallel ru, etc. Modulating from a yo key to the relative gu means using gu chords on yo roots. Modulating from yo to the parallel gu = using gu chords on wa roots. Going from yo zo to the relative gu = using gu7 or gu ru-6 chords on yo roots. Going to the relative ru = same chords on zo roots.
Temperament Names
Temperaments are named after the color of the comma(s) they temper out. Meantone = the green temperament = gT. 5-limit Porcupine = triple yo = y3T. 7-limit Porcupine = triple yo and ru = y3&rT. Each porcupine has a different name, thus color names provide more information. Both porcupines have the same pergen, third-4th, thus pergens group together similar temperaments.
The magnitude is part of the name: Schismic is LyT. The degree is as well, if the comma is not the smallest of the 7 ratios of that magnitude and color: Mavila is Ly1T and Father is g2T. The temperament name indicates the prime subgroup and the rank of the temperament. Thus ryyT is rank-3 because it has 2 explicit colors ru and yo and 2 implicit colors wa and clear, and 4 colors minus 1 comma = rank-3.
There are two ways to name multi-comma temperaments. The odd name minimizes the odd limit of the comma set, and the prime name minimizes the number and size of the primes used by each comma. The odd name for 7-limit Pajara is rryy&rT, and the prime name is sgg&rT. Often the two names are identical, e.g. y3&rT. The odd name is often shorter, and usually indicates commas more likely to be pumped. The prime name shows relationships between single-comma temperaments better. The question of which name to use is not yet fully resolved.
Ups and Downs, Lifts and Drops
Color notation merely renames ratios more conveniently, and strictly speaking, it only applies to just intonation. However, just as ratios can loosely describe edo notes, colors can be loosely applied to edos as well. A more precise application is to use ups and downs (^ and v) as "virtual colors", accidentals that always map to exactly one edostep. Notes are named up C sharp = ^C#. Ups and downs are used on the score just like color accidentals are. Intervals are named upmajor 3rd = ^M3, down 4th = v4, etc. Chords are named upminor 7th = ^m7, etc.
Rank-2 temperaments can be notated with ups and downs as well. Some require another accidental pair, lifts and drops (/ and \). See the pergens page.
(OBSOLETE LINKS, IGNORE THEM):