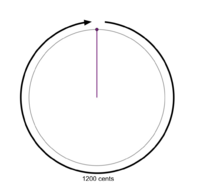
File:1-1 MOS Construction.png|An interval is chosen to be the period (the '''1200 cent octave''' in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise.
File:1-1 MOS Construction.png|An interval is chosen to be the period (the '''1200 cent octave''' in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise.
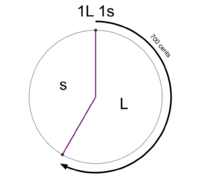
File:1-2 MOS Construction.png|An interval is chosen to be a generator (the '''700 cent perfect fifth''' in this example). This is the '''1L 1s''' MOS pattern.
File:1-2 MOS Construction.png|An interval is chosen to be a generator (the '''700 cent perfect fifth''' in this example). This is the '''[[1L 1s]]''' MOS pattern.
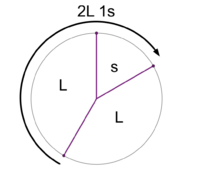
File:1-3 MOS Construction.png|Stacking the generator upon itself yields a scale with <u>2 step sizes</u>. This is the '''2L 1s''' MOS pattern.
File:1-3 MOS Construction.png|Stacking the generator upon itself yields a scale with <u>2 step sizes</u>. This is the '''[[2L 1s]]''' MOS pattern.
File:1-4 MOS Construction.png|Stacking the generator 2 times yields a scale with 3 step sizes ('''not MOS''').
File:1-4 MOS Construction.png|Stacking the generator 2 times yields a scale with 3 step sizes ('''not MOS''').
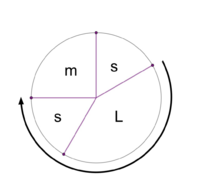
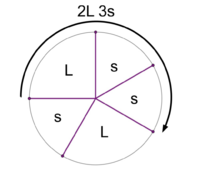
File:1-5 MOS Construction.png|Stacking the generator 3 times yields a scale with <u>2 step sizes</u>. This is the '''2L 3s''' MOS pattern.
File:1-5 MOS Construction.png|Stacking the generator 3 times yields a scale with <u>2 step sizes</u>. This is the '''[[2L 3s]]''' MOS pattern.
File:1-6 MOS Construction.png|Stacking the generator five times yields a scale with 3 step sizes ('''not MOS''').
File:1-6 MOS Construction.png|Stacking the generator five times yields a scale with 3 step sizes ('''not MOS''').
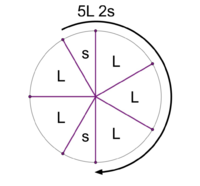
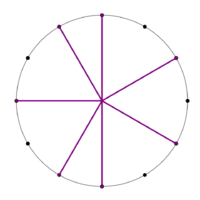
File:1-7 MOS Construction.png|Stacking the generator 6 times yields a scale with <u>2 step sizes</u>. This is the '''5L 2s''' MOS pattern.
File:1-7 MOS Construction.png|Stacking the generator 6 times yields a scale with <u>2 step sizes</u>. This is the '''[[5L 2s]]''' MOS pattern.
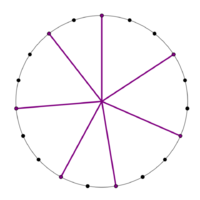
File:700centMOS.gif|The generator sequence animated with the moments of symmetry labelled.
File:700centMOS.gif|The generator sequence animated with the moments of symmetry labelled.
</gallery>
</gallery>
Line 17:
Line 17:
The [[step ratio]]—also referred to as the ''hardness''—of MOS denote the relative sizes of the large and small steps and is a key factor in classifying MOS patterns. A step ratio of 2:1, meaning the large steps are twice the size of the small steps, is considered the ''basic'' form of the MOS. When the difference between the large and small steps increases (i.e., the large step becomes larger and the small step smaller), the MOS is considered ''harder'', as the contrast in step sizes becomes more pronounced. Conversely, when the size difference decreases (i.e., the large step becomes smaller and the small step larger), the MOS is considered ''softer'', due to the more subtle contrast.
The [[step ratio]]—also referred to as the ''hardness''—of MOS denote the relative sizes of the large and small steps and is a key factor in classifying MOS patterns. A step ratio of 2:1, meaning the large steps are twice the size of the small steps, is considered the ''basic'' form of the MOS. When the difference between the large and small steps increases (i.e., the large step becomes larger and the small step smaller), the MOS is considered ''harder'', as the contrast in step sizes becomes more pronounced. Conversely, when the size difference decreases (i.e., the large step becomes smaller and the small step larger), the MOS is considered ''softer'', due to the more subtle contrast.
To find the equal tuning of some hardness of an MOS, simply input the relative size of the steps and multiply them by the number of steps. For example if we want to find the tuning which contains the 5L 2s pattern with the hardness of 2:1, we simply calculate 5(2)+2(1)=12, showing us that 12-EDO contains it.
To find the equal tuning that supports a given MOS pattern at a particular hardness, simply multiply the number of each step type by its relative size and sum the results. For example, for the 5L 2s pattern at a hardness of 2:1, calculate 5×2+2×1=12, showing that 12-EDO supports this pattern.
For a more thorough discussion on the spectrum of step ratios, please see [[TAMNAMS#Step ratio spectrum|TAMNAMS]].<gallery mode="nolines" widths="200" heights="200">
For a more thorough discussion on the spectrum of step ratios, please see [[TAMNAMS#Step ratio spectrum|TAMNAMS]].<gallery mode="nolines" widths="200" heights="200">
Line 26:
Line 28:
== Spectrum of MOS ==
== Spectrum of MOS ==
[[File:MOStest.gif|right|frameless]]
[[File:MOStest.gif|right|frameless]].
.
.
.
.
== Formal definitions and conditions of MOS ==
.
.
.
.
.
== See also ==
* [[Interval variety]]
* [[Step ratio]]
* [[TAMNAMS]]
* [[MODMOS]]
* [[MOS rhythm]]
== External links ==
* [https://www.anaphoria.com/wilsonintroMOS.html "Introduction to Moments of Symmetry"] in the ''[https://www.anaphoria.com/wilson.html Wilson Archives]'', hosted on [[Kraig Grady|Kraig Grady's]] website [[Anaphoria]]
* [https://www.wilsonic.co/ Wilsonic MTS-ESP and iOS apps] by [[Marcus Hobbs]]
* [https://wilson-tunings.netlify.app/moments-of-symmetry-v2 Moments of symmetry calculator (V2)] by [[Diego Villaseñor]]
* [https://www.anaphoria.com/MOSedo-app.html Moments of Symmetry in equal divisions of the octave calculator] by [[Billy Stiltner]]
* [https://untwelve.org/static/javascript_demos/MOSring_white.html Moment of Symmetry generator demo] by [[Aaron Krister Johnson]]
== References ==
Revision as of 19:34, 28 May 2025
WORK-IN-PROGRESS AS OF 27 MAY 2025
Moments of Symmetry (MOS) are scales created by a simple procedure that generates the common pentatonic and diatonic scales, but also a wide range of novel xenharmonic scales that share the same melodic coherence and structural balance. First described by Erv Wilson in the 1970's, the concept shares fundamental similarities and is often thought of as synonymous with the concept of Well-Formed scales, as well as the more generalized concept of MV2 scales. Over time, MOS have become a fundamental concept in xenharmonic theory, inspiring a wide range of musical uses, analytical approaches, and derivative concepts such as MODMOS, multi-MOS, and MOS-based rhythm.
An interval is chosen to be the period (the 1200 cent octave in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise.
An interval is chosen to be a generator (the 700 cent perfect fifth in this example). This is the 1L 1s MOS pattern.
Stacking the generator upon itself yields a scale with 2 step sizes. This is the 2L 1s MOS pattern.
Stacking the generator 2 times yields a scale with 3 step sizes (not MOS).
Stacking the generator 3 times yields a scale with 2 step sizes. This is the 2L 3s MOS pattern.
Stacking the generator five times yields a scale with 3 step sizes (not MOS).
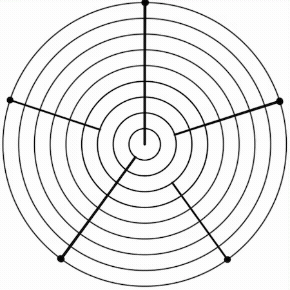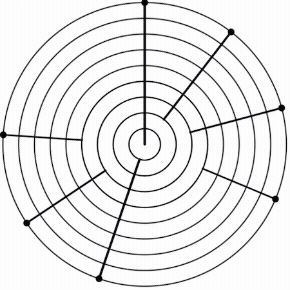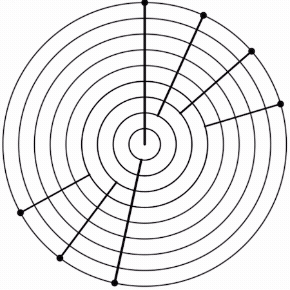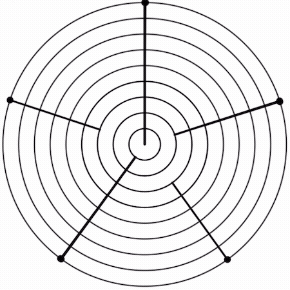
Stacking the generator 6 times yields a scale with 2 step sizes. This is the 5L 2s MOS pattern.
The generator sequence animated with the moments of symmetry labelled.
Step Ratios
The step ratio—also referred to as the hardness—of MOS denote the relative sizes of the large and small steps and is a key factor in classifying MOS patterns. A step ratio of 2:1, meaning the large steps are twice the size of the small steps, is considered the basic form of the MOS. When the difference between the large and small steps increases (i.e., the large step becomes larger and the small step smaller), the MOS is considered harder, as the contrast in step sizes becomes more pronounced. Conversely, when the size difference decreases (i.e., the large step becomes smaller and the small step larger), the MOS is considered softer, due to the more subtle contrast.
To find the equal tuning that supports a given MOS pattern at a particular hardness, simply multiply the number of each step type by its relative size and sum the results. For example, for the 5L 2s pattern at a hardness of 2:1, calculate 5×2+2×1=12, showing that 12-EDO supports this pattern.
For a more thorough discussion on the spectrum of step ratios, please see TAMNAMS.
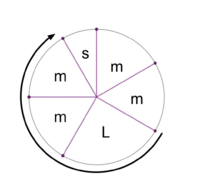
When the L:s ratio is 3:1, the MOS is hard. The hard 5L 2s is supported by 17-EDO.
When the L:s ratio is 2:1, the MOS is basic. The basic 5L 2s is supported by 12-EDO.
When the L:s ratio is 3:2, the MOS is soft. The soft 5L 2s is supported by 19-EDO..
An interval is chosen to be the period (the 1200 cent octave in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise.
An interval is chosen to be a generator (the 700 cent perfect fifth in this example). This is the 1L 1s MOS pattern.
Stacking the generator upon itself yields a scale with 2 step sizes. This is the 2L 1s MOS pattern.
Stacking the generator 2 times yields a scale with 3 step sizes (not MOS).
Stacking the generator 3 times yields a scale with 2 step sizes. This is the 2L 3s MOS pattern.
Stacking the generator five times yields a scale with 3 step sizes (not MOS).
Stacking the generator 6 times yields a scale with 2 step sizes. This is the 5L 2s MOS pattern.
The generator sequence animated with the moments of symmetry labelled.
When the L:s ratio is 3:1, the MOS is hard. The hard 5L 2s is supported by 17-EDO.
When the L:s ratio is 2:1, the MOS is basic. The basic 5L 2s is supported by 12-EDO.
When the L:s ratio is 3:2, the MOS is soft. The soft 5L 2s is supported by 19-EDO..
