User:CompactStar/Overtone scale: Difference between revisions
CompactStar (talk | contribs) Created page with "An '''ADO''' (arithmetic divisions of the octave) or '''overtone scale''' is a tuning system which divides the octave arithmetically rather than logarithmically. For any C-AD..." |
CompactStar (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
An '''ADO''' (arithmetic divisions of the octave) or '''overtone scale''' is a tuning system which divides the octave arithmetically rather than logarithmically. For any C-ADO system, the m-th degree is equal to the ratio (C+m)/C. For example, in [[12ado]] the first degree is [[13/12]], the second is 14/12 ([[7/6]]), and so on. For an ADO system, the distance between interval ratios is equal, rather than the distance between their logarithms like in EDO systems. All ADOs are subsets of [[just intonation]]. ADOs with more divisors such as [[Highly_composite_equal_division|highly composite]] ADOs generally have more useful just intervals. | An '''ADO''' (arithmetic divisions of the octave) or '''overtone scale''' is a tuning system which divides the octave arithmetically rather than logarithmically. This is equivalent to taking an octave-long subset of the harmonic series and make it repeat at the octave. For any C-ADO system, the m-th degree is equal to the ratio (C+m)/C. For example, in [[12ado]] the first degree is [[13/12]], the second is 14/12 ([[7/6]]), and so on. For an ADO system, the distance between interval ratios is equal, rather than the distance between their logarithms like in EDO systems. All ADOs are subsets of [[just intonation]]. ADOs with more divisors such as [[Highly_composite_equal_division|highly composite]] ADOs generally have more useful just intervals. | ||
If the first division is <math>R_1</math> (which is ratio of C/C) and the last , <math>R_n</math> (which is ratio of 2C/C), with common difference of d | If the first division is <math>R_1</math> (which is ratio of C/C) and the last , <math>R_n</math> (which is ratio of 2C/C), with common difference of d | ||
Revision as of 04:05, 2 March 2023
An ADO (arithmetic divisions of the octave) or overtone scale is a tuning system which divides the octave arithmetically rather than logarithmically. This is equivalent to taking an octave-long subset of the harmonic series and make it repeat at the octave. For any C-ADO system, the m-th degree is equal to the ratio (C+m)/C. For example, in 12ado the first degree is 13/12, the second is 14/12 (7/6), and so on. For an ADO system, the distance between interval ratios is equal, rather than the distance between their logarithms like in EDO systems. All ADOs are subsets of just intonation. ADOs with more divisors such as highly composite ADOs generally have more useful just intervals.
If the first division is [math]\displaystyle{ R_1 }[/math] (which is ratio of C/C) and the last , [math]\displaystyle{ R_n }[/math] (which is ratio of 2C/C), with common difference of d
(which is 1/C), we have :
[math]\displaystyle{ R_2 = R_1 + d \\ R_3= R_1 + 2d \\ R_4 = R_1 + 3d \\ \vdots \\ R_n = R_1 + (n-1)d }[/math]
Lengths
If the first division has ratio of R1 and length of L1 and the last, Rn and Ln , we have: Ln = 1/Rn and if Rn >........> R3 > R2 > R1 so :
L1 > L2 > L3 > …… > Ln
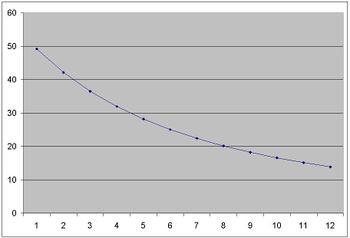
This lengths are related to reverse of ratios in system.The above picture shows the differences between divisions of length in 12-ADO system . On the contrary , we have equal divisios of length in **EDL system**:

Relation to superparticular ratios
An ADO has step sizes of superparticular ratios with increasing numerators. For example, 5ado has step sizes of 6/5, 7/6, 8/7, and 9/8.
Relation to otonality & harmonic series
We can consider ADO system as otonal system. Otonality is a term introduced by Harry Partch to describe chords whose notes are the overtones (multiples) of a given fixed tone.Considering ADO , an Otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an otonality because they can be written as 4/4, 5/4, 6/4. Every Otonality is therefore part of the harmonic series. An otonality corresponds to an arithmetic series of frequencies or a harmonic series of wavelengths or distances on a string instrument.
Individual pages for ADOs
- 2ado
- 3ado
- 4ado
- 5ado
- 6ado
- 7ado
- 8ado
- 9ado
- 10ado
- 11ado
- 12ado
- 13ado
- 14ado
- 15ado
- 20ado
- 30ado
- 60ado
- 120ado
See also
- Arithmetic temperament
- Arithmetic MOS scale
- Fret position calculator (excel sheet) based on EDL system and string length
- How to approximate EDO and ADO systems with each other? Download this file
- Magic of Tone and the Art of Music by the late Dane Rhudyar
- OD, or otonal division: An n-ADO is equivalent to an n-ODO.