AFDO

ADO (arithmetic divisions of the octave) is a tuning system which divides the octave arithmetically rather than logarithmically. For any C-ADO system, the m-th degree is equal to the ratio (C+m)/C. For example, in 12-ADO the first degree is 13/12, the second is 14/12 (7/6), and so on. For an ADO system, the distance between ratios is equal, rater than the distance between their logarithms like in EDO systems.

If the first division is [math]\displaystyle{ R_1 }[/math] (which is ratio of C/C) and the last , [math]\displaystyle{ R_n }[/math] (which is ratio of 2C/C), with common difference of d

(which is 1/C), we have :

[math]\displaystyle{ R_2 = R_1 + d \\ R_3= R_1 + 2d \\ R_4 = R_1 + 3d \\ \vdots \\ R_n = R_1 + (n-1)d }[/math]

If the first division has ratio of R1 and length of L1 and the last, Rn and Ln , we have: Ln = 1/Rn and if Rn >........> R3 > R2 > R1 so :

L1 > L2 > L3 > …… > Ln

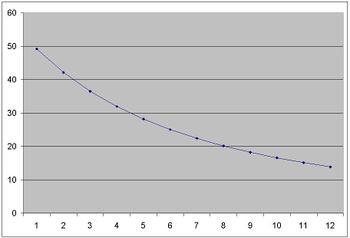
This lengths are related to reverse of ratios in system.The above picture shows the differences between divisions of length in 12-ADO system . On the contrary , we have equal divisios of length in **EDL system**:

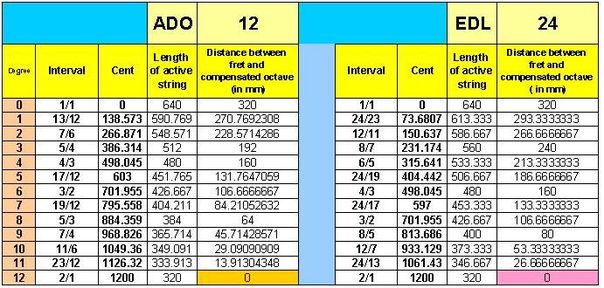
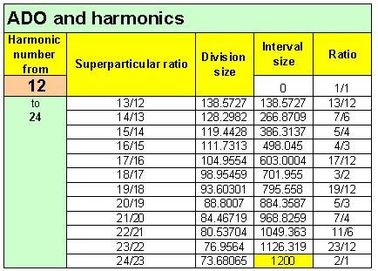
Relation between harmonics and ADO system

ADO (like EDL) is based on **Superparticular ratios** and **harmonic series**. Have a look at 12-ADO in this picture:

The above picture shows that ADO system is classified as :

• System with unequal **epimorios** (**Superparticular**) divisions.
• System based on ascending series of superparticular ratios with descending sizes.
• System which covers superparticular ratios between harmonic of number C (in this example 12)to harmonic of Number 2C(in this example 24).
• An spreadsheet showing relation between harmonics , superparticular ratios and ADO system

Relation between Otonality and ADO system

We can consider ADO system as **Otonal system** .Otonality is a term introduced by **Harry Partch** to describe chords whose notes are the overtones (multiples) of a given fixed tone.Considering ADO , an Otonality is a collection of pitches which can be expressed in ratios that have equal denominators. For example, 1/1, 5/4, and 3/2 form an Otonality because they can be written as 4/4, 5/4, 6/4. Every Otonality is therefore part of the **harmonic series**. nominator here is called "**Numerary nexus**".An Otonality corresponds to an **arithmetic series** of frequencies or a **harmonic series** of wavelengths or distances on a **string instrument**.

- Fret position calculator (excel sheet ) based on EDL system and string length

- How to approximate EDO and ADO systems with each other?Download this file

Related to ADO

**Magic of Tone and the Art of Music by the late Dane Rhudyar**

OD, or otonal division: An n-ADO is equivalent to an n-ODO.