Kite's color notation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
This is | This is the "crash course". For a full explanation, see [[KiteGiedraitis|Kite's]] book, [http://www.tallkite.com/AlternativeTunings.html "Alternative Tunings: Theory, Notation and Practice"]. | ||
== Color Names == | == Color Names for 3, 5 and 7 == | ||
Every prime above 3 has two color names, one for '''over''' (prime in the numerator) and one for '''under''' (prime in the denominator). Over colors end with -o, and under colors with -u. Here's the colors for primes 3, 5 and 7: | Every prime above 3 has two color names, one for '''over''' (prime in the numerator) and one for '''under''' (prime in the denominator). Over colors end with -o, and under colors with -u. Here's the colors for primes 3, 5 and 7: | ||
| Line 15: | Line 15: | ||
The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Azure is used instead of blue because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom. | The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Azure is used instead of blue because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom. | ||
== Interval Names == | == Interval Names == | ||
| Line 30: | Line 25: | ||
21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g<sup>3</sup>2. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd. | 21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g<sup>3</sup>2. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd. | ||
Remote intervals are '''large''' (fifthward) and '''small''' (fourthward), abbreviated L and s. '''Central''' means neither large nor small. The '''magnitude''' is found by adding up all the monzo exponents except the first one, dividing by 7, and rounding off. 0 = central, 1 = large, 2 = double large, etc. 81/64 = Lw3, 135/128 = Ly1. Magnitudes do not add up predictably like colors and degrees do: w2 + w2 = Lw3. | |||
[[File:Lattice41a.png|731x731px]] | [[File:Lattice41a.png|731x731px]] | ||
A comma is 10-50¢, a '''minicomma''' is 1-10¢, and a '''microcomma''' is 0-1¢. | A '''comma''' is 10-50¢, a '''minicomma''' is 1-10¢, and a '''microcomma''' is 0-1¢. These categories allow us to omit the magnitude in the spoken name. Thus sgg2 is not the small gugu 2nd, but simply the gugu comma. The double-large wa negative 2nd (the pyth comma) is simply the wa comma. 81/80 = g1 is the gu comma. LLg-2 = g1 + LLw-2 is also gu and also a comma, but LLg-2 is not <u>the</u> gu comma , because its odd limit is so much higher. | ||
See [[Gallery of Just Intervals]] for more examples of interval names. | See the [[Gallery of Just Intervals]] for more examples of interval names. | ||
== Note Names == | == Note Names == | ||
Notes are named zE♭, yyG#, etc. spoken as "zo E flat", "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa. The relative-notation lattice above can be superimposed on | Notes are named zE♭, yyG#, etc. spoken as "zo E flat", "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa. The relative-notation lattice above can be superimposed on this absolute-notation lattice to name every note. Thus D + y3 = yF#, and from yE to ryF# = r2. | ||
[[File:Lattice51.png|frameless|810x810px]] | [[File:Lattice51.png|frameless|810x810px]] | ||
== Prime Subgroup Names == | |||
Just as wa means 3-all or 3-limit, '''ya''' means 5-all and includes wa, yo, gu, yoyo, gugu, etc. Ya = the 2.3.5 prime subgroup = 5-limit. '''Za''' = 7-all = 2.3.7. Yaza = 2.3.5.7 = 7-limit. '''Nowa''' means without wa, and yaza nowa = 2.5.7. | |||
Prime 2 (even more colorless than wa) is clear, abbreviated '''ca''', and yaza noca = 3.5.7. 2-limit intervals like 2/1 are called wa not clear, for simplicity. | |||
== Color Names for Higher Primes == | |||
Colors for primes greater than 7 are named after the number itself: | |||
'''Lova''' = 11-over, '''lu''' = 11-under, and '''la''' = 11-all = 2.3.11. (Lova not lo, because "lo C" sounds like "low C".) Lova and lu are abbreviated to '''1o''' and '''1u''' on the score and in interval names and chord names, e.g. lova A = 1oA, lova 4th = 1o4 = 11/8 and C lova-7 = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both lova and lu, since they are only 7.1¢ apart (implying the [http://x31eq.com/cgi-bin/rt.cgi?ets=24_17&limit=2_3_11 Neuter] temperament). More precisely, lova notes could be called lovender, and lu notes could be called luvender. Both are shades of lavender. | |||
'''Tho''' = 13-over, '''thu''' = 13-under, and '''tha''' = 13-all. Tho and thu are abbreviated as '''3o''' and '''3u''' on the score and in interval names, e.g. 13/8 = 3o6 = tho 6th. | |||
Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13. and yazalatha = 2.3.5.7.11.13 = the full 13-limit. | |||
While the note 11/8 above C can be written two ways, either as 1oF or as 1oF#, the interval 11/8 can only be written one way, as 1o4. Likewise, 13/8 above C is either 3oA or 3oA♭, but 13/8 is only 3o6. <u>This is the rationale for using large/small rather than major/minor</u>. Intervals names and chord names become unambiguous for la and tha intervals. Also, commonly used intervals and chords get concise names: gu 3rd not gu minor 3rd, Ag not Agm, etc. On the score and in note names, the 1o accidental either raises by 33/32 or lowers by 729/704. The meaning will usually be clear from context, however it's safer to write at the top of the page either "1o4 = P4" or "1o4 = A4". Likewise, 3o6 should be noted as either m6 or M6. | |||
'''So''' = 17-over, '''su''' = 17-under, and '''sa''' = 17-all, abbreviated as '''17o''' and '''17u'''. '''Sova''' is an alternate form of so, to distinguish it from the solfege syllable Sol. | |||
'''Nova''' = 19-over, '''nunda''' = 19-under, '''na''' = 19-all, abbreviated as '''19o''' and '''19u'''. Nova because "no 3rd" could mean either 19/16 or thirdless. Nunda because "the nu key" sounds like "the new key". 12edo implies yasana = 2.3.5.17.19. | |||
'''Twenty-tho''' = 23-over, '''twenty-thu''' = 23-under, '''twenty-tha''' =23-all, abbreviated as '''23o''', '''23u''' and '''23a'''. 2.3.5.7.23 = yaza23a = "yaza-twenty-tha". | |||
'''Twenty-no/-nu/-na''' = 29o/29u/29a, '''thirty-wo/-wu/-wa''' = 31o/31u/31a, '''thirty-so/-su/-sa''' = 37o/37u/37a, etc. | |||
The alternate forms with -ova or -unda are only needed when the color word appears alone, and confusion is possible. Thus 11/7 = loru 5th, not lovaru 5th, and 29o = twenty-no, not twenty-nova. | |||
== Chord Names == | == Chord Names == | ||
| Line 54: | Line 75: | ||
The y,z7 chord is also called the h7 chord ("aitch-seven"), because it's part of the harmonic series. The s7 ("sub-seven") chord is part of the subharmonic series. It's the first 7 subharmonics, with the 3rd subharmonic becoming the root. Note that s7 has no 7th. There are h9 chords, s11 chords, etc. | The y,z7 chord is also called the h7 chord ("aitch-seven"), because it's part of the harmonic series. The s7 ("sub-seven") chord is part of the subharmonic series. It's the first 7 subharmonics, with the 3rd subharmonic becoming the root. Note that s7 has no 7th. There are h9 chords, s11 chords, etc. | ||
Alterations are in parentheses, additions never are. Example: Ch7(zg5)zg9 = C yE zgG♭ zB♭ zgD♭. Omissions are indicated by "no", as in Ch11no3. In harmonic and subharmonic chords, the 3 refers to the degree, not the 3rd harmonic. However numbers ≥ 15 always refer to (sub)harmonics, as in Ch15 | <u>Alterations are in parentheses</u>, additions never are. Example: Ch7(zg5)zg9 = C yE zgG♭ zB♭ zgD♭. Omissions are indicated by "no", as in Ch11no3. In harmonic and subharmonic chords, the 3 refers to the degree, not the 3rd harmonic. However numbers ≥ 15 always refer to (sub)harmonics, as in Ch15. | ||
An 11th implies a 3rd, 5th, 7th and 9th. A 13th implies all these plus an 11th. The 5th, 9th and/or 13th default to wa. The 6th, 7th, and/or 11th defaults to the color of the 3rd. Thus a y13 chord = w1 y3 w5 y7 w9 y11 w13. However, an add 11 chord defaults to a wa 11: Cz7,11 = w1 z3 w5 z7 w11 | |||
== Staff notation == | == Staff notation == | ||
Notes on the staff default to wa. Non-wa notes have a color accidental like g, ry, etc. Like conventional sharp/flat accidentals, they apply to every such note in the measure and in the same octave. Unlike conventional accidentals which apply to a note (e.g. A), color accidentals only apply to one specific "version" of that note (e.g. A flat or A natural). For example, the yo accidental in the first chord applies to all the D naturals in that measure, but not to the D flats. | |||
[[File: | [[File:Notation example 1.png|frameless|781x781px]] | ||
Staff notation can optionally include a color signature written above the staff. This makes color notation more similar to Johnston notation. | |||
[[File:Notation example 2.png|786x786px]] | |||
== | Color notation can optionally be made more similar to Sagittal notation by including two more accidentals, p and q (long forms po and qu = "ku"), to indicate raising/lowering by a pythagorean comma. For example, yF# = ypG♭, and zE♭= zqD#. This allows trills to always be written as a 2nd.[[File:Notation example 5a.png|992x992px]] | ||
== Chord Progressions, Keys and Modulations == | |||
The tonic is always wa. The root of each chord has a color, which defaults to wa. C - Am - F - G would be Cy - yAg - Fy - Gy. | |||
In relative notation, the I, IV and V chords default to a wa root. II, III, VI and VII <u>must</u> have an explicit root-color. gCy - gGy - Ag becomes gIIIy - gVIIy - Ig. | |||
In adaptive JI, chords are just, but roots move by tempered intervals. Comma pumps are indicated with brackets: Cy - yAg - [y=w]Dg - Gy - Cy. | |||
Keys are named after the colors used. The B♭h7 - E♭h7 - B♭h7 - Fh9 example above is in B♭ yo zo. Analogous to the relative and parallel major or minor, one can modulate to relative gu, parallel ru, etc. Modulating from a yo key to the relative gu means using gu chords on yo roots. Modulating from yo to the parallel gu = using gu chords on wa roots. Going from yo zo to the relative gu = using gu7 or gu ru-6 chords on yo roots. Going to the relative ru = same chords on zo roots. | |||
== Temperament Names == | |||
Temperaments are named after the color of the comma(s) they temper out. Meantone = the green temperament = gT. 5-limit Porcupine = triple yo = y<sup>3</sup>T. 7-limit Porcupine = triple yo and ru = y<sup>3</sup>&rT. Each porcupine has a different name, thus color names provide more information. Both porcupines have the same [[pergen]], third-4th, thus pergens group together similar temperaments. | |||
The magnitude is part of the name: Schismic is LyT. The degree is as well, if the comma is not the smallest of the 7 ratios of that magnitude and color: Mavila is Ly1T and Father is g2T. The temperament name indicates the prime subgroup and the rank of the temperament. Thus ryyT is rank-3 because it has 2 explicit colors ru and yo and 2 implicit colors wa and clear, and 4 colors minus 1 comma = rank-3. | |||
There are two ways to name multi-comma temperaments. The odd name minimizes the odd limit of the comma set, and the prime name minimizes the number and size of the primes used by each comma. The odd name for 7-limit [[Pajara]] is rryy&rT, and the prime name is sgg&rT. Often the two names are identical, e.g. y<sup>3</sup>&rT. The odd name is often shorter, and usually indicates commas more likely to be pumped. The prime name shows relationships between single-comma temperaments better. The question of which name to use is not yet fully resolved. | |||
== Ups and Downs, Lifts and Drops == | |||
Color notation merely renames ratios in a more convenient form, and strictly speaking, it only applies to just intonation. However, just as ratios can loosely describe edo notes, colors can be loosely applied to edos as well. A more precise application is to use ups and downs (^ and v) as "virtual colors" that always map to exactly one edostep. | |||
=='''<u>FULL EXPLANATION</u>:'''== | =='''<u>FULL EXPLANATION</u>:'''== | ||
Revision as of 06:02, 16 October 2018
This is the "crash course". For a full explanation, see Kite's book, "Alternative Tunings: Theory, Notation and Practice".
Color Names for 3, 5 and 7
Every prime above 3 has two color names, one for over (prime in the numerator) and one for under (prime in the denominator). Over colors end with -o, and under colors with -u. Here's the colors for primes 3, 5 and 7:
Wa = white (strong but colorless) = 3-limit
Yo = yellow (warm and sunny) = 5-over = major
Gu ("goo") = green (not as bright as yellow) = 5-under = minor
Zo = blue/azure (dark and bluesy) = 7-over = subminor
Ru = red (alarming, inflamed) = 7-under = supermajor
The colors come in a red-yellow-green-blue rainbow, with warm/cool colors indicating sharp/flat intervals. The rainbow of 3rds runs 9/7 - 5/4 - 6/5 - 7/6. Azure is used instead of blue because b looks like a flat sign. Mnemonic: Z looks like 7 with an extra line on the bottom.
Interval Names
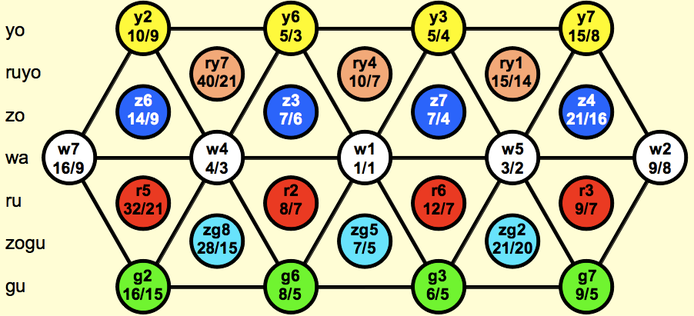
A color and a degree indicates a ratio, and vice versa. Every ratio has a spoken name and a written name. For 3/2, they are wa 5th and w5. Colors and degrees always add up predictably: z3 + g3 = zg5 = zogu 5th. Zogu not guzo, higher primes always come first. Opposite colors cancel: y3 + g3 = w5.
The JI lattice consists of many lattice rows, each one a chain of 5ths. Each lattice row has its own color, and each color has its own lattice row.
21/10 = zogu 9th = zg9. 25/16 = yoyo 5th = yy5. 128/125 = triple gu 2nd = g32. 50/49 = double ruyo negative 2nd = rryy-2. It's a negative 2nd because it goes up in pitch but down the scale: zg5 + rryy-2 = ry4. Negative is different than descending, from ry4 to zg5 is a descending negative 2nd.
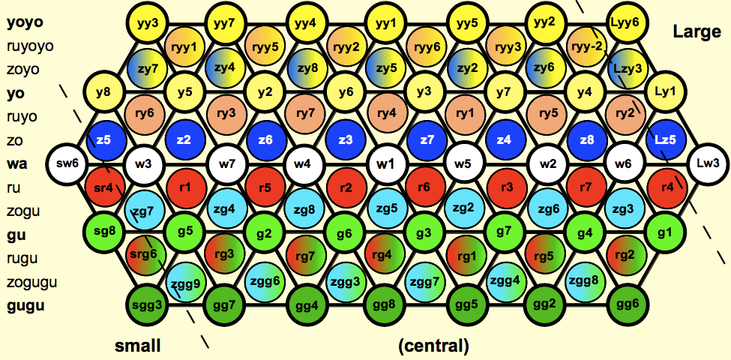
Remote intervals are large (fifthward) and small (fourthward), abbreviated L and s. Central means neither large nor small. The magnitude is found by adding up all the monzo exponents except the first one, dividing by 7, and rounding off. 0 = central, 1 = large, 2 = double large, etc. 81/64 = Lw3, 135/128 = Ly1. Magnitudes do not add up predictably like colors and degrees do: w2 + w2 = Lw3.
A comma is 10-50¢, a minicomma is 1-10¢, and a microcomma is 0-1¢. These categories allow us to omit the magnitude in the spoken name. Thus sgg2 is not the small gugu 2nd, but simply the gugu comma. The double-large wa negative 2nd (the pyth comma) is simply the wa comma. 81/80 = g1 is the gu comma. LLg-2 = g1 + LLw-2 is also gu and also a comma, but LLg-2 is not the gu comma , because its odd limit is so much higher.
See the Gallery of Just Intervals for more examples of interval names.
Note Names
Notes are named zE♭, yyG#, etc. spoken as "zo E flat", "yoyo G sharp". Notes are never large or small, only intervals are. Uncolored notes default to wa. The relative-notation lattice above can be superimposed on this absolute-notation lattice to name every note. Thus D + y3 = yF#, and from yE to ryF# = r2.
Prime Subgroup Names
Just as wa means 3-all or 3-limit, ya means 5-all and includes wa, yo, gu, yoyo, gugu, etc. Ya = the 2.3.5 prime subgroup = 5-limit. Za = 7-all = 2.3.7. Yaza = 2.3.5.7 = 7-limit. Nowa means without wa, and yaza nowa = 2.5.7.
Prime 2 (even more colorless than wa) is clear, abbreviated ca, and yaza noca = 3.5.7. 2-limit intervals like 2/1 are called wa not clear, for simplicity.
Color Names for Higher Primes
Colors for primes greater than 7 are named after the number itself:
Lova = 11-over, lu = 11-under, and la = 11-all = 2.3.11. (Lova not lo, because "lo C" sounds like "low C".) Lova and lu are abbreviated to 1o and 1u on the score and in interval names and chord names, e.g. lova A = 1oA, lova 4th = 1o4 = 11/8 and C lova-7 = C1o7 = 1/1 - 11/9 - 3/2 - 11/6. The associated color is lavender (mnemonic: "e-leven-der"), which refers to both lova and lu, since they are only 7.1¢ apart (implying the Neuter temperament). More precisely, lova notes could be called lovender, and lu notes could be called luvender. Both are shades of lavender.
Tho = 13-over, thu = 13-under, and tha = 13-all. Tho and thu are abbreviated as 3o and 3u on the score and in interval names, e.g. 13/8 = 3o6 = tho 6th.
Prime subgroups: yala = 2.3.5.11, zalatha nowa = 2.7.11.13. and yazalatha = 2.3.5.7.11.13 = the full 13-limit.
While the note 11/8 above C can be written two ways, either as 1oF or as 1oF#, the interval 11/8 can only be written one way, as 1o4. Likewise, 13/8 above C is either 3oA or 3oA♭, but 13/8 is only 3o6. This is the rationale for using large/small rather than major/minor. Intervals names and chord names become unambiguous for la and tha intervals. Also, commonly used intervals and chords get concise names: gu 3rd not gu minor 3rd, Ag not Agm, etc. On the score and in note names, the 1o accidental either raises by 33/32 or lowers by 729/704. The meaning will usually be clear from context, however it's safer to write at the top of the page either "1o4 = P4" or "1o4 = A4". Likewise, 3o6 should be noted as either m6 or M6.
So = 17-over, su = 17-under, and sa = 17-all, abbreviated as 17o and 17u. Sova is an alternate form of so, to distinguish it from the solfege syllable Sol.
Nova = 19-over, nunda = 19-under, na = 19-all, abbreviated as 19o and 19u. Nova because "no 3rd" could mean either 19/16 or thirdless. Nunda because "the nu key" sounds like "the new key". 12edo implies yasana = 2.3.5.17.19.
Twenty-tho = 23-over, twenty-thu = 23-under, twenty-tha =23-all, abbreviated as 23o, 23u and 23a. 2.3.5.7.23 = yaza23a = "yaza-twenty-tha".
Twenty-no/-nu/-na = 29o/29u/29a, thirty-wo/-wu/-wa = 31o/31u/31a, thirty-so/-su/-sa = 37o/37u/37a, etc.
The alternate forms with -ova or -unda are only needed when the color word appears alone, and confusion is possible. Thus 11/7 = loru 5th, not lovaru 5th, and 29o = twenty-no, not twenty-nova.
Chord Names
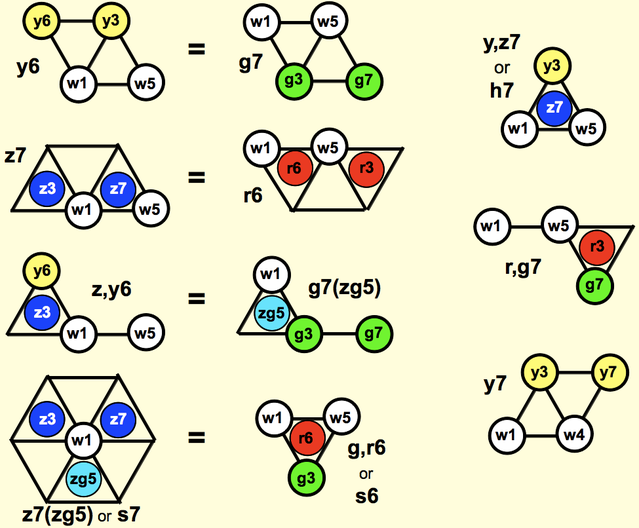
Triads are named after their 3rd, e.g. Cy. "Yo C" is a note, "C yo" is a chord. The four main yaza triads:
If the root isn't wa, the root color is added to the interval color: yo A gu = yAg = yA + (w1 g3 w5) = yA + wC + yE.
Tetrads are named Cy6, Dg7, etc. The 11 main yaza tetrads, with chord homonyms (same shape, different root) equated:
The y,z7 chord is also called the h7 chord ("aitch-seven"), because it's part of the harmonic series. The s7 ("sub-seven") chord is part of the subharmonic series. It's the first 7 subharmonics, with the 3rd subharmonic becoming the root. Note that s7 has no 7th. There are h9 chords, s11 chords, etc.
Alterations are in parentheses, additions never are. Example: Ch7(zg5)zg9 = C yE zgG♭ zB♭ zgD♭. Omissions are indicated by "no", as in Ch11no3. In harmonic and subharmonic chords, the 3 refers to the degree, not the 3rd harmonic. However numbers ≥ 15 always refer to (sub)harmonics, as in Ch15.
An 11th implies a 3rd, 5th, 7th and 9th. A 13th implies all these plus an 11th. The 5th, 9th and/or 13th default to wa. The 6th, 7th, and/or 11th defaults to the color of the 3rd. Thus a y13 chord = w1 y3 w5 y7 w9 y11 w13. However, an add 11 chord defaults to a wa 11: Cz7,11 = w1 z3 w5 z7 w11
Staff notation
Notes on the staff default to wa. Non-wa notes have a color accidental like g, ry, etc. Like conventional sharp/flat accidentals, they apply to every such note in the measure and in the same octave. Unlike conventional accidentals which apply to a note (e.g. A), color accidentals only apply to one specific "version" of that note (e.g. A flat or A natural). For example, the yo accidental in the first chord applies to all the D naturals in that measure, but not to the D flats.
Staff notation can optionally include a color signature written above the staff. This makes color notation more similar to Johnston notation.
Color notation can optionally be made more similar to Sagittal notation by including two more accidentals, p and q (long forms po and qu = "ku"), to indicate raising/lowering by a pythagorean comma. For example, yF# = ypG♭, and zE♭= zqD#. This allows trills to always be written as a 2nd.
Chord Progressions, Keys and Modulations
The tonic is always wa. The root of each chord has a color, which defaults to wa. C - Am - F - G would be Cy - yAg - Fy - Gy.
In relative notation, the I, IV and V chords default to a wa root. II, III, VI and VII must have an explicit root-color. gCy - gGy - Ag becomes gIIIy - gVIIy - Ig.
In adaptive JI, chords are just, but roots move by tempered intervals. Comma pumps are indicated with brackets: Cy - yAg - [y=w]Dg - Gy - Cy.
Keys are named after the colors used. The B♭h7 - E♭h7 - B♭h7 - Fh9 example above is in B♭ yo zo. Analogous to the relative and parallel major or minor, one can modulate to relative gu, parallel ru, etc. Modulating from a yo key to the relative gu means using gu chords on yo roots. Modulating from yo to the parallel gu = using gu chords on wa roots. Going from yo zo to the relative gu = using gu7 or gu ru-6 chords on yo roots. Going to the relative ru = same chords on zo roots.
Temperament Names
Temperaments are named after the color of the comma(s) they temper out. Meantone = the green temperament = gT. 5-limit Porcupine = triple yo = y3T. 7-limit Porcupine = triple yo and ru = y3&rT. Each porcupine has a different name, thus color names provide more information. Both porcupines have the same pergen, third-4th, thus pergens group together similar temperaments.
The magnitude is part of the name: Schismic is LyT. The degree is as well, if the comma is not the smallest of the 7 ratios of that magnitude and color: Mavila is Ly1T and Father is g2T. The temperament name indicates the prime subgroup and the rank of the temperament. Thus ryyT is rank-3 because it has 2 explicit colors ru and yo and 2 implicit colors wa and clear, and 4 colors minus 1 comma = rank-3.
There are two ways to name multi-comma temperaments. The odd name minimizes the odd limit of the comma set, and the prime name minimizes the number and size of the primes used by each comma. The odd name for 7-limit Pajara is rryy&rT, and the prime name is sgg&rT. Often the two names are identical, e.g. y3&rT. The odd name is often shorter, and usually indicates commas more likely to be pumped. The prime name shows relationships between single-comma temperaments better. The question of which name to use is not yet fully resolved.
Ups and Downs, Lifts and Drops
Color notation merely renames ratios in a more convenient form, and strictly speaking, it only applies to just intonation. However, just as ratios can loosely describe edo notes, colors can be loosely applied to edos as well. A more precise application is to use ups and downs (^ and v) as "virtual colors" that always map to exactly one edostep.