OTC 12L 7s: Difference between revisions

Latest revision as of 03:08, 24 June 2025

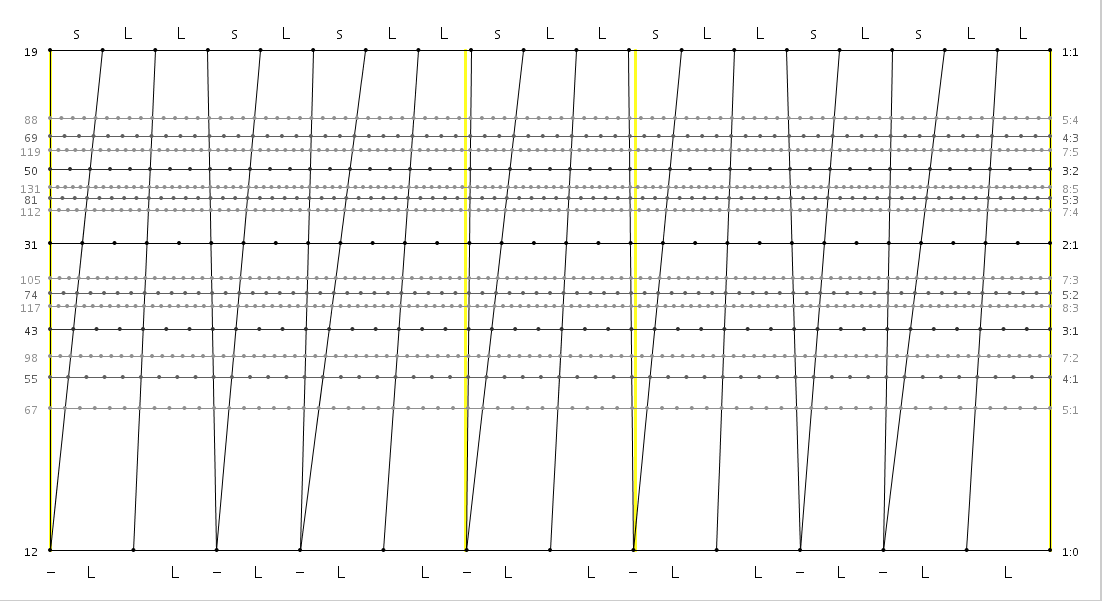
Omnitetrachordal MOS scale

19 tones (8+3+8)

Meantone MOS; P<0 (oddly, neither this scale nor its dual can be tuned with a perfect 3/2!)

P = -4.8459060415

Q = 20.7295302077 (4/3 = 5L+2.5s)

L = 63.16 to 100.00 cents (97.26 cents @ Q)

s = 0.00 to 63.16 cents (4.69 cents @ Q)

9/8 = 2L+s (189.47 to 200.00 cents)

4/3 = 5L+3s (500.00 to 505.26 cents)

generator = 4/3

notable EDOs: 31, 43, 50, 55

symmetric mode: LsLLsLsLLsLLsLsLLsL

all modes:

Noted as omnitetrachordal by Paul Erlich no later than 2002. See tuning-math list messages 3685 and 10987.

@@ Line 114: / Line 114: @@
 <ul><li>Noted as omnitetrachordal by Paul Erlich no later than 2002. See tuning-math list messages [http://robertinventor.com/tuning-math/s___4/msg_3675-3699.html#3685 3685] and [http://robertinventor.com/tuning-math/s__11/msg_10975-10999.html#10987 10987].</li></ul>
 [[Category:19-tone scales]]
-[[Category:Tempered_scales]]
+[[Category:Tempered scales]]
 [[Category:Pages with mostly numerical content]]
 [[Category:MODMOS]]
 [[Category:Omnitetrachordal]]
 [[Category:Meantone]]