137edo: Difference between revisions
Jump to navigation
Jump to search
Wikispaces>FREEZE No edit summary |
m cat rename |
||
| Line 5: | Line 5: | ||
[[File:137edo_MOS_031_demo_correction.png|alt=137edo_MOS_031_demo_correction.png|137edo_MOS_031_demo_correction.png]] | [[File:137edo_MOS_031_demo_correction.png|alt=137edo_MOS_031_demo_correction.png|137edo_MOS_031_demo_correction.png]] | ||
[[:File:137edo_MOS_031.svg|137edo_MOS_031.svg]] | [[:File:137edo_MOS_031.svg|137edo_MOS_031.svg]] | ||
[[Category: | |||
[[Category: | [[Category:Edo]] | ||
[[Category: | [[Category:Nuwell]] | ||
[[Category: | [[Category:Orwell]] | ||
[[Category:Prime EDO]] | |||
[[Category:Semicomma]] | |||
Revision as of 10:19, 2 November 2018
The 137 equal division divides the octave into 137 equal parts of 8.759 cents each. It is the optimal patent val for 7-limit orwell temperament and for the planar temperament tempering out 2430/2401. It tempers out 2109375/2097152 (the semicomma) in the 5-limit; 225/224 and 1728/1715 in the 7-limit; 243/242 in the 11-limit; 351/350 in the 13-limit; 375/374 and 442/441 in the 17-limit; and 324/323 and 495/494 in the 19-limit. Since it is the 33rd prime number, 137edo has no proper divisors aside from 1.
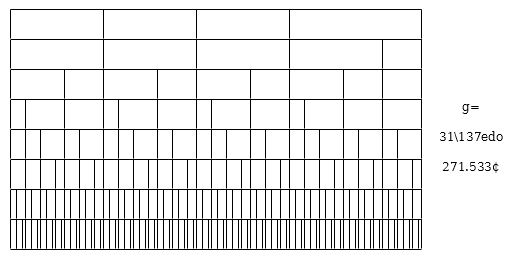
A diagram of 7-limit Orwell based on the 31\137edo generator: