Scale tree: Difference between revisions
m →See also: Add sharpness |
No edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{ | {{Wikipedia|Stern–Brocot tree}} | ||
The '''scale tree''' is an infinite binary tree that lists every possible interval in an equal tuning, assuming a given equave (on this page, the octave). It is the xenharmonic application, commonly used in the context of [[MOS scale|MOS scales]] and [[regular temperament theory]], of the Stern-Brocot tree, an infinite tree containing every (positive, reduced) rational number. | |||
The '''scale tree''' | |||
== Structure == | |||
The scale tree is a diagram of every EDO interval, but it can be taken as a chart of EDOs based on their best approximations of some interval in particular, for example tunings of the perfect fifth. | |||
Any branching point on the scale tree (that is, any unique edo interval) is the root of a ''kite.'' Visually on the diagram, the kite of an interval is the rightmost branch of its left child and the leftmost branch of its right child, which forms the distinctive "kite" shape from which the concept get its name. The fact that [[Kite Giedraitis]] references the concept extensively is a coincidence. Theory-wise, the kite is the set of edo intervals that produce the closest approximations to the circle of the root interval for their size, being sharp or flat by a single edostep for their edo where the root interval would close the circle. For example, the 7\12 kite contains 11\19 and 10\17, but not 13\22 and 15\26 as those end up off by 2 edosteps. | |||
== Diagrams == | |||
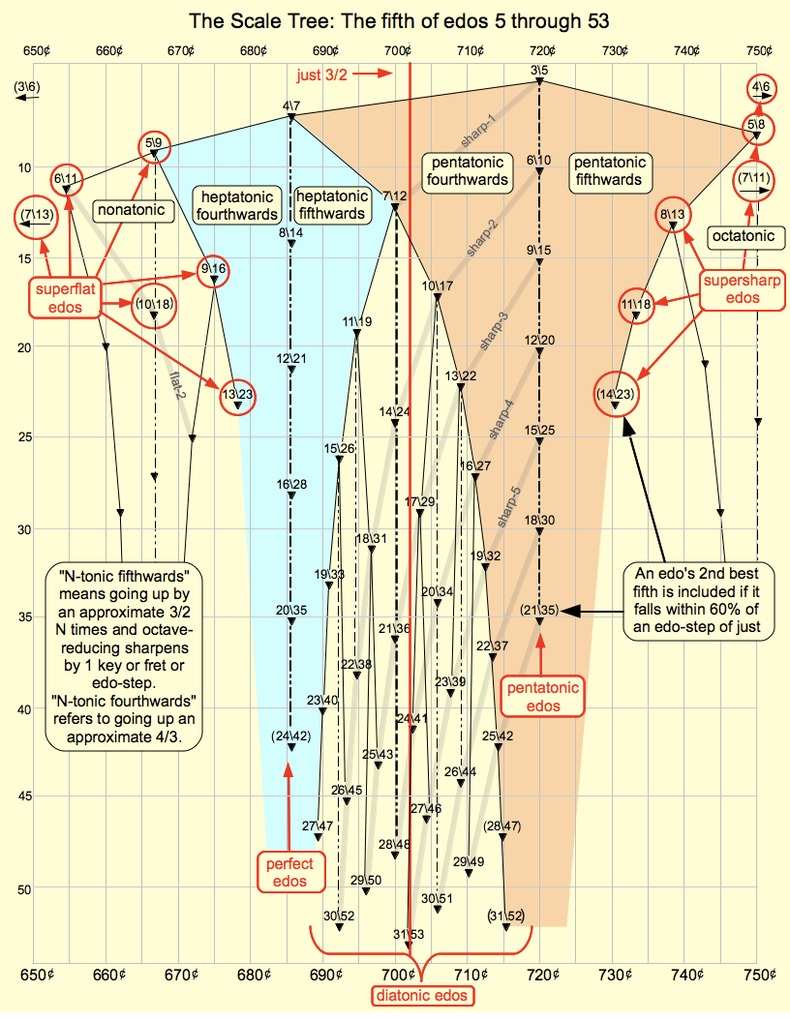
The scale tree provides a visual map of the world of EDOs, based on fifth size. Two kites are colored here: the pentatonic (3\5) and heptatonic (4\7) kites. | |||
[[File:The_Scale_Tree.png|800x1023px|The Scale Tree.png]] | |||
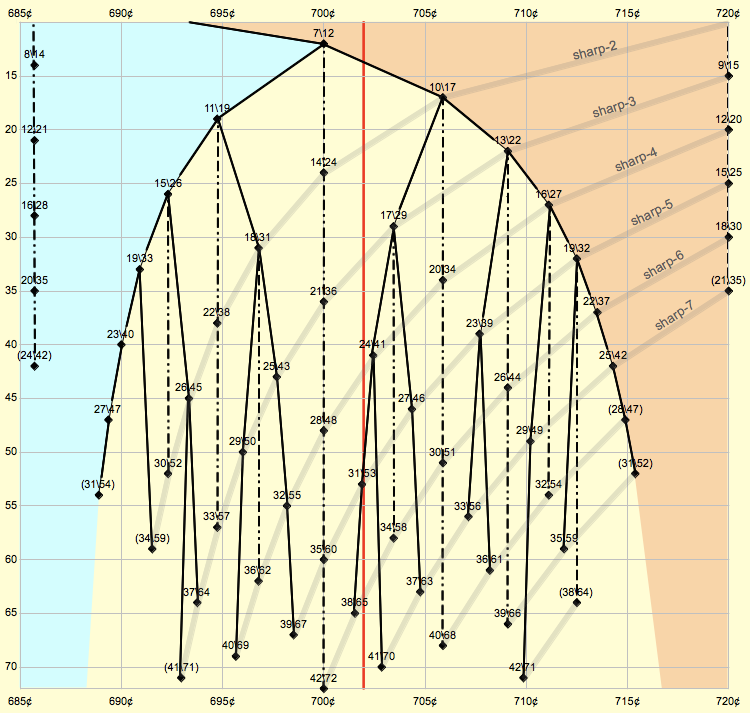
The regular EDOs, up to 72edo: | |||
[[File:Scale_Tree_close-up.png|Scale Tree close-up.png]] | |||
== Construction == | == Construction == | ||
The easiest way of producing the scale tree is by finding the [[Mediant|mediants]] | The easiest way of producing the scale tree for the intervals within the octave is by finding the [[Mediant|mediants]] of adjacent ratios, starting with 0\1 (the unison, 0 steps of 1edo) and 1\1 (the octave, 1 step of 1edo). One can also use 0\1 (zero cents) and 1\0 (infinite cents) to get every possible ascending edo interval. Then, treat the logarithmic ratios as normal fractions and proceed take the mediant, which is 1\2 (the semioctave), putting it in between. The next level of the tree contains these ratios, as well as the next mediants 1\3 and 2\3 (the major third and minor sixth of 12edo). This process can be repeated to produce a tree of any depth. Note that these are actually logarithmic ratios, and should be written with a backslash (¥) instead of a forward slash. | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! Level 1 | |||
! Level 2 | |||
! Level 3 | |||
! Level 4 | |||
|- | |- | ||
| | | 0\1 | ||
| | | 0\1 | ||
| | | 0\1 | ||
|1 | | 0\1 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
|1 | | 1\4 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | 1\3 | ||
| | | 1\3 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 2\5 | ||
|- | |- | ||
| | | | ||
| | | 1\2 | ||
| | | 1\2 | ||
| | | 1\2 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 3\5 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | 2\3 | ||
|3 | | 2\3 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 3\4 | ||
|- | |- | ||
| | | 1\1 | ||
| 1\1 | |||
| 1\1 | |||
| 1\1 | |||
| | |||
|1 | |||
|1 | |||
|} | |} | ||
If | |||
If duplicate ratios in successive levels are removed, the tree structure becomes more apparent. | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! Level 1 | |||
! Level 2 | |||
! Level 3 | |||
! Level 4 | |||
|- | |- | ||
| | | 0\1 | ||
| | |||
| | | | ||
| | | | ||
| | |||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 1\4 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | 1\3 | ||
| | |||
| | |||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 2\5 | ||
|- | |- | ||
| | | | ||
| | | 1\2 | ||
| | |||
| | | | ||
| | |||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 3\5 | ||
|- | |- | ||
| | | | ||
| | | | ||
| | | 2\3 | ||
| | |||
| | |||
|- | |- | ||
| | | | ||
| | | | ||
| | | | ||
| | | 3\4 | ||
|- | |- | ||
|1 | | 1\1 | ||
| | |||
| | | | ||
| | | | ||
| | |||
|} | |} | ||
The two starting intervals of 0\1 and 1\1 may be replaced with any other edo intervals to produce a new tree that is a subset of the original tree, where the mediant of those ratios represents the root. | |||
== See also == | == See also == | ||
* [[MOS Scale Family Tree|MOS family tree]], a similar tree for organizing MOS scales by production rules. | * [[MOS Scale Family Tree|MOS family tree]], a similar tree for organizing MOS scales by production rules. | ||
* [[Sharpness]] | * [[Sharpness]] | ||
{{Todo| expand| comment=This page is a work-in-progress; feel free to edit as needed.<br />Idea: give musical examples instead of the 0/1 to 1/0 case, which can be found on Wikipedia. <br>Idea: add a section explaining what “kites” are. | inline=1}} | |||
[[Category:Scale]] | [[Category:Scale]] | ||
Latest revision as of 01:25, 19 August 2025
The scale tree is an infinite binary tree that lists every possible interval in an equal tuning, assuming a given equave (on this page, the octave). It is the xenharmonic application, commonly used in the context of MOS scales and regular temperament theory, of the Stern-Brocot tree, an infinite tree containing every (positive, reduced) rational number.
Structure
The scale tree is a diagram of every EDO interval, but it can be taken as a chart of EDOs based on their best approximations of some interval in particular, for example tunings of the perfect fifth.
Any branching point on the scale tree (that is, any unique edo interval) is the root of a kite. Visually on the diagram, the kite of an interval is the rightmost branch of its left child and the leftmost branch of its right child, which forms the distinctive "kite" shape from which the concept get its name. The fact that Kite Giedraitis references the concept extensively is a coincidence. Theory-wise, the kite is the set of edo intervals that produce the closest approximations to the circle of the root interval for their size, being sharp or flat by a single edostep for their edo where the root interval would close the circle. For example, the 7\12 kite contains 11\19 and 10\17, but not 13\22 and 15\26 as those end up off by 2 edosteps.
Diagrams
The scale tree provides a visual map of the world of EDOs, based on fifth size. Two kites are colored here: the pentatonic (3\5) and heptatonic (4\7) kites.
The regular EDOs, up to 72edo:
Construction
The easiest way of producing the scale tree for the intervals within the octave is by finding the mediants of adjacent ratios, starting with 0\1 (the unison, 0 steps of 1edo) and 1\1 (the octave, 1 step of 1edo). One can also use 0\1 (zero cents) and 1\0 (infinite cents) to get every possible ascending edo interval. Then, treat the logarithmic ratios as normal fractions and proceed take the mediant, which is 1\2 (the semioctave), putting it in between. The next level of the tree contains these ratios, as well as the next mediants 1\3 and 2\3 (the major third and minor sixth of 12edo). This process can be repeated to produce a tree of any depth. Note that these are actually logarithmic ratios, and should be written with a backslash (¥) instead of a forward slash.
| Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|
| 0\1 | 0\1 | 0\1 | 0\1 |
| 1\4 | |||
| 1\3 | 1\3 | ||
| 2\5 | |||
| 1\2 | 1\2 | 1\2 | |
| 3\5 | |||
| 2\3 | 2\3 | ||
| 3\4 | |||
| 1\1 | 1\1 | 1\1 | 1\1 |
If duplicate ratios in successive levels are removed, the tree structure becomes more apparent.
| Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|
| 0\1 | |||
| 1\4 | |||
| 1\3 | |||
| 2\5 | |||
| 1\2 | |||
| 3\5 | |||
| 2\3 | |||
| 3\4 | |||
| 1\1 |
The two starting intervals of 0\1 and 1\1 may be replaced with any other edo intervals to produce a new tree that is a subset of the original tree, where the mediant of those ratios represents the root.
See also
- MOS family tree, a similar tree for organizing MOS scales by production rules.
- Sharpness