|
|
| (7 intermediate revisions by 5 users not shown) |
| Line 1: |
Line 1: |
| <h2>IMPORTED REVISION FROM WIKISPACES</h2>
| | {{todo|inline=1|cleanup|comment=If it is deprecated and cannot be updated, then just add the [[Template:Deprecated]] message box to the top of the page and delete this todo notice}} |
| This is an imported revision from Wikispaces. The revision metadata is included below for reference:<br>
| |
| : This revision was by author [[User:x31eq|x31eq]] and made on <tt>2013-03-31 11:32:20 UTC</tt>.<br>
| |
| : The original revision id was <tt>419047982</tt>.<br>
| |
| : The revision comment was: <tt></tt><br>
| |
| The revision contents are below, presented both in the original Wikispaces Wikitext format, and in HTML exactly as Wikispaces rendered it.<br>
| |
| <h4>Original Wikitext content:</h4>
| |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;white-space: pre-wrap ! important" class="old-revision-html"><span style="color: #000000; font-family: arial,sans-serif; font-size: 18px;">**Arithmetic irrational divisions**</span>
| |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">For an intervallic system with </span>__<span style="color: black; font-size: 11pt;">n</span>__<span style="color: black; font-size: 11pt;"> divisions , </span><span style="color: #be00ff; font-size: 11pt;">[[http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29|AID_]]</span><span style="color: black; font-size: 11pt;"> is considered as [[http://www.richland.edu/james/lecture/m116/sequences/arithmetic.html|arithmetic sequence]] with divisions of system as terms of sequence. </span></span>
| | ==Arithmetic irrational divisions== |
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; text-align: left;"><span style="color: black; font-size: 11pt;"> If the first division is </span>__<span style="color: black; font-size: 11pt;">A1</span>__<span style="color: black; font-size: 11pt;"> and the last , </span>__<span style="color: black; font-size: 11pt;">An</span>__<span style="color: black; font-size: 11pt;"> , with common difference of </span>__<span style="color: black; font-size: 11pt;">d</span>__<span style="color: black; font-size: 11pt;"> , we have : </span></span>
| |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">A1 = A1</span>
| |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A2 = A1+d </span>
| |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A3= A1+2d </span>
| |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A4 = A1+3d</span>
| |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">……… </span>
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;">An = A1+(n-1)d</span>
| |
|
| |
|
| <span style="direction: ltr; font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">So sum of the divisions is </span>__<span style="color: black; font-size: 11pt;">Sn</span>__<span style="color: black; font-size: 11pt;"> :</span></span>
| | For an intervallic system with <u>n</u> divisions, [http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 AID] is considered as [http://www.richland.edu/james/lecture/m116/sequences/arithmetic.html arithmetic sequence] with divisions of system as terms of sequence. |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;">**<span style="color: black; font-size: 11pt;">Sn =( __n[2A1+(n-1)d])/2__</span>**</span>
| | If the first division is <u>A1</u> and the last, <u>An</u> , with common difference of <u>d</u> , we have : |
| | :: A1 = A1 |
| | :: A2 = A1+d |
| | :: A3 = A1+2d |
| | :: A4 = A1+3d |
| | :: ... |
| | :: An = A1+(n-1)d |
|
| |
|
| | So sum of the divisions is <u>Sn</u> : |
| | :: '''Sn =( <u>n[2A1+(n-1)d])/2</u>''' |
|
| |
|
|
| |
|
| <span style="direction: ltr; display: block; text-align: left;"><span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;"> As we can consider </span>__<span style="color: black; font-size: 11pt;">Sn</span>__<span style="color: black; font-size: 11pt;"> of system to be 1200 cent or anything else (octavic or non-octavic system ) then </span>__<span style="color: black; font-size: 11pt;">d</span>__<span style="color: black; font-size: 11pt;"> is most important to make an AID with n divisions with A1.</span></span><span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;"> So, the common difference between divisions is : </span></span>
| | As we can consider <u>Sn</u> of system to be 1200 cent or anything else (octavic or non-octavic system ) then <u>d</u> is most important to make an AID with n divisions with A1. So, the common difference between divisions is : |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;">**<span style="color: black; font-size: 11pt;">d =( __2(Sn - nA1))/((n(n-1))__</span>**</span>
| | :: '''d =( <u>2(Sn - nA1))/(n(n-1))</u>''' |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">By considering Sn=1200 , A1=70 , n=12 , d will be 5.454545455 and our 12-tone scale is equal to:</span>
| | By considering Sn=1200, A1=70, n=12, d will be 5.454545455 and our 12-tone scale is equal to: |
| <span style="font-family: Tahoma,Geneva,sans-serif;">[[#TOC-0.070.0145.455226.364312.727404.545]] **0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0**</span>
| | :: '''0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0''' |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">Scales based on AID can be subsets of EDO if :</span><span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">1- we choose d=0 so ,<span style="color: black; font-size: 11pt;"> A1 = Sn/n</span> .. Consider </span>__<span style="color: black; font-size: 10pt;">n</span>__<span style="color: black; font-size: 10pt;">=8 and </span>__<span style="color: black; font-size: 10pt;">A1</span>__<span style="color: black; font-size: 10pt;">=150 , then we have 8-EDO .</span></span>
| |
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">2- for a constant </span>__<span style="color: black; font-size: 10pt;">n</span>__<span style="color: black; font-size: 10pt;"> and different __A1__, if __d__ and (Sn/A1) are Integer number , we have a susbet of EDO or EDI( Equal divisions of Interval) .Consider __Sn = 1400__ , </span>__<span style="color: black; font-size: 10pt;">n</span>__<span style="color: black; font-size: 10pt;">=8 and </span>__<span style="color: black; font-size: 10pt;">A1</span>__<span style="color: black; font-size: 10pt;">=70 , then we have a subset of a 140-ED(1400.) with Degrees as [[tel/7 17 30 46 65 87 112|7 17 30 46 65 87 112]] 140 :</span></span>
| |
| **0.000 70.000 170.000 300.000 460.000 650.000 870.000 1120.000 1400.000**
| |
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif;">[[#TOC-And-now-for:]]And now for </span><span style="font-family: Tahoma,Geneva,sans-serif;">Sn=1400 and n=8,</span>
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> [[#TOC-If-A1-175.0-then-we-have-8-AID-1400]]If A1=175.0 then we have 8-AID(1400.)</span>
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> [[#TOC-If-A1-56-then-we-have-700-AID-1400.]]If A1=56 then we have 700-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> [[tel/28 73 135 214 310|28 73 135 214 310]] [[tel/423 553 700|423 553 700]]</span></span>
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> [[#TOC-If-A1-87.5-then-we-have-112-AID-140]]<span style="color: black; font-size: 10pt;">If A1=87.5 then we have 112-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> [[tel/7 16 27 40 55 72 91|7 16 27 40 55 72 91]] 112</span></span></span>
| |
|
| |
|
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;">__AID__ sytem shows different ascending , descending or linear trend of change in divisions sizes due to relation between n and A1 in __AID__<span style="color: black; font-size: 10pt;"> and __EDO__ with equal degree:</span></span>
| | Scales based on AID can be subsets of [[EDO]] if: |
| * <span style="font-family: Tahoma,Geneva,sans-serif;">If choosing __<span style="color: black; font-size: 10pt;">A1</span>__<span style="color: black; font-size: 10pt;"> greater than division size in equal degree </span>__<span style="color: black; font-size: 10pt;">EDO</span>__<span style="color: black; font-size: 10pt;"> , </span>__<span style="color: black; font-size: 10pt;">d</span>__<span style="color: black; font-size: 10pt;"> is negative and </span>__<span style="color: black; font-size: 10pt;">AID</span>__<span style="color: black; font-size: 10pt;"> is descending.</span></span>
| | # we choose d=0 so, A1 = Sn/n .. Consider <u>n</u>=8 and <u>A1</u>=150, then we have [[8edo|8-EDO]] . |
| * <span style="font-family: Tahoma,Geneva,sans-serif;">If choosing __<span style="color: black; font-size: 10pt;">A1</span>__<span style="color: black; font-size: 10pt;"> smaller than division size in equal degree </span>__<span style="color: black; font-size: 10pt;">EDO</span>__<span style="color: black; font-size: 10pt;"> , </span>__<span style="color: black; font-size: 10pt;">d</span>__<span style="color: black; font-size: 10pt;"> is positive and </span>__<span style="color: black; font-size: 10pt;">AID</span>__<span style="color: black; font-size: 10pt;"> is ascending.</span></span>
| | # for a constant <u>n</u> and different <u>A1</u>, if <u>d</u> and (Sn/A1) are integers, we have a subset of EDO or [[Equal-step tuning|EDI (Equal divisions of Interval)]]. |
| * <span style="font-family: Tahoma,Geneva,sans-serif;">If choosing __<span style="color: black; font-size: 10pt;">A1</span>__<span style="color: black; font-size: 10pt;"> equal to division size in equal degree </span>__<span style="color: black; font-size: 10pt;">EDO</span>__<span style="color: black; font-size: 10pt;"> , </span>__<span style="color: black; font-size: 10pt;">d</span>__<span style="color: black; font-size: 10pt;"> is zero.</span>**</span>
| |
|
| |
|
| [[image:http://sites.google.com/site/240edo/AIDO-custom-size-298-402.jpg align="center"]]
| | Consider <u>Sn = 1400</u> , <u>n</u>=8 and <u>A1</u>=70, then we have a subset of a 140-ED (1400.) with Degrees as 7 17 30 46 65 87 112 140 : |
| | :: 0.0 70.0 170.0 300.0 460.0 650.0 870.0 1120.0 1400.0 |
|
| |
|
| ==<span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 13.3333px;">171.4285714 is point of intersection in these 3 trends:</span>== | | And now for Sn=1400 and n=8, |
| | * If A1=175.0 then we have 8-AID(1400.) |
| | * If A1=56 then we have 700-AID(1400.) with Degrees as 28 73 135 214 310 423 553 700 |
| | * If A1=87.5 then we have 112-AID(1400.) with Degrees as 7 16 27 40 55 72 91 112 |
|
| |
|
| | AID system shows different ascending, descending or linear trend of change in divisions sizes due to relation between n and A1 in AID and EDO with equal degree: |
| | * If choosing <u>A1</u> greater than division size in equal degree EDO, <u>d</u> is negative and <u>AID</u> is descending. |
| | * If choosing <u>A1</u> smaller than division size in equal degree EDO, <u>d</u> is positive and <u>AID</u> is ascending. |
| | * If choosing <u>A1</u> equal to division size in equal degree EDO, <u>d</u> is zero. |
|
| |
|
| [[image:http://sites.google.com/site/240edo/AIDO2.jpg align="center"]] | | [[file:AIDO-custom-size-298-402.jpg]] |
| we can have different kinds of AID:
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;">__<span style="color: #000000; font-family: arial,sans-serif;">AIDO = Arithmetic irrational divisions of octave</span>__</span>
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;">__<span style="color: #000000; font-family: arial,sans-serif;">AIDINO = Arithmetic irrational divisions of irrational non-octave</span>__</span>
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;">__<span style="color: #000000; font-family: arial,sans-serif;">AIDRNO = Arithmetic irrational divisions of rational non-octave</span>__</span>
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;">__<span style="color: #000000; font-family: arial,sans-serif;">AIDRI = Arithmetic irrational divisions of rational interval</span>__</span>
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;">__<span style="color: #000000; font-family: arial,sans-serif;">AIDII = Arithmetic irrational divisions of irrational interval</span>__</span>
| |
|
| |
|
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 12px; text-decoration: none;">[[http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29|**Example : Baran scale**]]</span></pre></div>
| | |
| <h4>Original HTML content:</h4>
| | 171.4285714 is point of intersection in these 3 trends: |
| <div style="width:100%; max-height:400pt; overflow:auto; background-color:#f8f9fa; border: 1px solid #eaecf0; padding:0em"><pre style="margin:0px;border:none;background:none;word-wrap:break-word;width:200%;white-space: pre-wrap ! important" class="old-revision-html"><html><head><title>AID</title></head><body><span style="color: #000000; font-family: arial,sans-serif; font-size: 18px;"><strong>Arithmetic irrational divisions</strong></span><br />
| | |
| <br />
| | [[file:AIDO2.jpg]] |
| <span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">For an intervallic system with </span><u><span style="color: black; font-size: 11pt;">n</span></u><span style="color: black; font-size: 11pt;"> divisions , </span><span style="color: #be00ff; font-size: 11pt;"><a class="wiki_link_ext" href="http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29" rel="nofollow">AID_</a></span><span style="color: black; font-size: 11pt;"> is considered as <a class="wiki_link_ext" href="http://www.richland.edu/james/lecture/m116/sequences/arithmetic.html" rel="nofollow">arithmetic sequence</a> with divisions of system as terms of sequence. </span></span><br />
| | |
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; text-align: left;"><span style="color: black; font-size: 11pt;"> If the first division is </span><u><span style="color: black; font-size: 11pt;">A1</span></u><span style="color: black; font-size: 11pt;"> and the last , </span><u><span style="color: black; font-size: 11pt;">An</span></u><span style="color: black; font-size: 11pt;"> , with common difference of </span><u><span style="color: black; font-size: 11pt;">d</span></u><span style="color: black; font-size: 11pt;"> , we have : </span></span><br />
| | |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">A1 = A1</span><br />
| | We can have different kinds of AID: |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A2 = A1+d </span><br />
| | |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A3= A1+2d </span><br />
| | * AIDO = Arithmetic irrational divisions of octave |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A4 = A1+3d</span><br />
| | * AIDINO = Arithmetic irrational divisions of irrational non-octave |
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">……… </span><br />
| | * AIDRNO = Arithmetic irrational divisions of rational non-octave |
| <span style="font-family: Tahoma,Geneva,sans-serif;">An = A1+(n-1)d</span><br />
| | * AIDRI = Arithmetic irrational divisions of rational interval |
| <br />
| | * AIDII = Arithmetic irrational divisions of irrational interval |
| <span style="direction: ltr; font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">So sum of the divisions is </span><u><span style="color: black; font-size: 11pt;">Sn</span></u><span style="color: black; font-size: 11pt;"> :</span></span><br />
| | |
| <br />
| | Example: [http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 Baran scale] |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;"><strong><span style="color: black; font-size: 11pt;">Sn =( <u>n[2A1+(n-1)d])/2</u></span></strong></span><br />
| | |
| <br />
| | [[Category:AID]] |
| <br />
| | [[Category:Shaahin Mohajeri]] |
| <br />
| |
| <span style="direction: ltr; display: block; text-align: left;"><span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;"> As we can consider </span><u><span style="color: black; font-size: 11pt;">Sn</span></u><span style="color: black; font-size: 11pt;"> of system to be 1200 cent or anything else (octavic or non-octavic system ) then </span><u><span style="color: black; font-size: 11pt;">d</span></u><span style="color: black; font-size: 11pt;"> is most important to make an AID with n divisions with A1.</span></span><span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;"> So, the common difference between divisions is : </span></span><br />
| |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;"><strong><span style="color: black; font-size: 11pt;">d =( <u>2(Sn - nA1))/((n(n-1))</u></span></strong></span><br />
| |
| <br />
| |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">By considering Sn=1200 , A1=70 , n=12 , d will be 5.454545455 and our 12-tone scale is equal to:</span><br />
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"><!-- ws:start:WikiTextAnchorRule:2:&lt;img src=&quot;/i/anchor.gif&quot; class=&quot;WikiAnchor&quot; alt=&quot;Anchor&quot; id=&quot;wikitext@@anchor@@TOC-0.070.0145.455226.364312.727404.545&quot; title=&quot;Anchor: TOC-0.070.0145.455226.364312.727404.545&quot;/&gt; --><a name="TOC-0.070.0145.455226.364312.727404.545"></a><!-- ws:end:WikiTextAnchorRule:2 --> <strong>0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0</strong></span><br />
| |
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">Scales based on AID can be subsets of EDO if :</span><span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">1- we choose d=0 so ,<span style="color: black; font-size: 11pt;"> A1 = Sn/n</span> .. Consider </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;">=8 and </span><u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;">=150 , then we have 8-EDO .</span></span><br />
| |
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">2- for a constant </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;"> and different <u>A1</u>, if <u>d</u> and (Sn/A1) are Integer number , we have a susbet of EDO or EDI( Equal divisions of Interval) .Consider <u>Sn = 1400</u> , </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;">=8 and </span><u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;">=70 , then we have a subset of a 140-ED(1400.) with Degrees as <a class="wiki_link" href="http://tel.wikispaces.com/7%2017%2030%2046%2065%2087%20112">7 17 30 46 65 87 112</a> 140 :</span></span><br />
| |
| <strong>0.000 70.000 170.000 300.000 460.000 650.000 870.000 1120.000 1400.000</strong><br />
| |
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif;"><!-- ws:start:WikiTextAnchorRule:3:&lt;img src=&quot;/i/anchor.gif&quot; class=&quot;WikiAnchor&quot; alt=&quot;Anchor&quot; id=&quot;wikitext@@anchor@@TOC-And-now-for:&quot; title=&quot;Anchor: TOC-And-now-for:&quot;/&gt; --><a name="TOC-And-now-for:"></a><!-- ws:end:WikiTextAnchorRule:3 -->And now for </span><span style="font-family: Tahoma,Geneva,sans-serif;">Sn=1400 and n=8,</span><br />
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> <!-- ws:start:WikiTextAnchorRule:4:&lt;img src=&quot;/i/anchor.gif&quot; class=&quot;WikiAnchor&quot; alt=&quot;Anchor&quot; id=&quot;wikitext@@anchor@@TOC-If-A1-175.0-then-we-have-8-AID-1400&quot; title=&quot;Anchor: TOC-If-A1-175.0-then-we-have-8-AID-1400&quot;/&gt; --><a name="TOC-If-A1-175.0-then-we-have-8-AID-1400"></a><!-- ws:end:WikiTextAnchorRule:4 -->If A1=175.0 then we have 8-AID(1400.)</span><br />
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> <!-- ws:start:WikiTextAnchorRule:5:&lt;img src=&quot;/i/anchor.gif&quot; class=&quot;WikiAnchor&quot; alt=&quot;Anchor&quot; id=&quot;wikitext@@anchor@@TOC-If-A1-56-then-we-have-700-AID-1400.&quot; title=&quot;Anchor: TOC-If-A1-56-then-we-have-700-AID-1400.&quot;/&gt; --><a name="TOC-If-A1-56-then-we-have-700-AID-1400."></a><!-- ws:end:WikiTextAnchorRule:5 -->If A1=56 then we have 700-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> <a class="wiki_link" href="http://tel.wikispaces.com/28%2073%20135%20214%20310">28 73 135 214 310</a> <a class="wiki_link" href="http://tel.wikispaces.com/423%20553%20700">423 553 700</a></span></span><br />
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> <!-- ws:start:WikiTextAnchorRule:6:&lt;img src=&quot;/i/anchor.gif&quot; class=&quot;WikiAnchor&quot; alt=&quot;Anchor&quot; id=&quot;wikitext@@anchor@@TOC-If-A1-87.5-then-we-have-112-AID-140&quot; title=&quot;Anchor: TOC-If-A1-87.5-then-we-have-112-AID-140&quot;/&gt; --><a name="TOC-If-A1-87.5-then-we-have-112-AID-140"></a><!-- ws:end:WikiTextAnchorRule:6 --><span style="color: black; font-size: 10pt;">If A1=87.5 then we have 112-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> <a class="wiki_link" href="http://tel.wikispaces.com/7%2016%2027%2040%2055%2072%2091">7 16 27 40 55 72 91</a> 112</span></span></span><br />
| |
| <br />
| |
| <br />
| |
| <span style="font-family: Tahoma,Geneva,sans-serif;"><u>AID</u> sytem shows different ascending , descending or linear trend of change in divisions sizes due to relation between n and A1 in <u>AID</u><span style="color: black; font-size: 10pt;"> and <u>EDO</u> with equal degree:</span></span><br />
| |
| <ul><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> greater than division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is negative and </span><u><span style="color: black; font-size: 10pt;">AID</span></u><span style="color: black; font-size: 10pt;"> is descending.</span></span></li><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> smaller than division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is positive and </span><u><span style="color: black; font-size: 10pt;">AID</span></u><span style="color: black; font-size: 10pt;"> is ascending.</span></span></li><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> equal to division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is zero.</span>**</span></li></ul><br />
| |
| <!-- ws:start:WikiTextRemoteImageRule:15:&lt;div style=&quot;text-align: center&quot;&gt;&lt;img src=&quot;http://sites.google.com/site/240edo/AIDO-custom-size-298-402.jpg&quot; alt=&quot;&quot; title=&quot;&quot; /&gt;&lt;/div&gt; --><div style="text-align: center"><img src="http://sites.google.com/site/240edo/AIDO-custom-size-298-402.jpg" alt="external image AIDO-custom-size-298-402.jpg" title="external image AIDO-custom-size-298-402.jpg" /></div><!-- ws:end:WikiTextRemoteImageRule:15 --><br />
| |
| <!-- ws:start:WikiTextHeadingRule:0:&lt;h2&gt; --><h2 id="toc0"><a name="x-171.4285714 is point of intersection in these 3 trends:"></a><!-- ws:end:WikiTextHeadingRule:0 --><span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 13.3333px;">171.4285714 is point of intersection in these 3 trends:</span></h2>
| |
| <br />
| |
| <br />
| |
| <!-- ws:start:WikiTextRemoteImageRule:16:&lt;div style=&quot;text-align: center&quot;&gt;&lt;img src=&quot;http://sites.google.com/site/240edo/AIDO2.jpg&quot; alt=&quot;&quot; title=&quot;&quot; /&gt;&lt;/div&gt; --><div style="text-align: center"><img src="http://sites.google.com/site/240edo/AIDO2.jpg" alt="external image AIDO2.jpg" title="external image AIDO2.jpg" /></div><!-- ws:end:WikiTextRemoteImageRule:16 -->we can have different kinds of AID:<br />
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDO = Arithmetic irrational divisions of octave</span></u></span><br />
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDINO = Arithmetic irrational divisions of irrational non-octave</span></u></span><br />
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDRNO = Arithmetic irrational divisions of rational non-octave</span></u></span><br />
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDRI = Arithmetic irrational divisions of rational interval</span></u></span><br />
| |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDII = Arithmetic irrational divisions of irrational interval</span></u></span><br />
| |
| <br />
| |
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 12px; text-decoration: none;"><a class="wiki_link_ext" href="http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29" rel="nofollow">**Example : Baran scale**</a></span></body></html></pre></div>
| |
|
Todo: cleanup
If it is deprecated and cannot be updated, then just add the Template:Deprecated message box to the top of the page and delete this todo notice
|
Arithmetic irrational divisions
For an intervallic system with n divisions, AID is considered as arithmetic sequence with divisions of system as terms of sequence.
If the first division is A1 and the last, An , with common difference of d , we have :
- A1 = A1
- A2 = A1+d
- A3 = A1+2d
- A4 = A1+3d
- ...
- An = A1+(n-1)d
So sum of the divisions is Sn :
- Sn =( n[2A1+(n-1)d])/2
As we can consider Sn of system to be 1200 cent or anything else (octavic or non-octavic system ) then d is most important to make an AID with n divisions with A1. So, the common difference between divisions is :
- d =( 2(Sn - nA1))/(n(n-1))
By considering Sn=1200, A1=70, n=12, d will be 5.454545455 and our 12-tone scale is equal to:
- 0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0
Scales based on AID can be subsets of EDO if:
- we choose d=0 so, A1 = Sn/n .. Consider n=8 and A1=150, then we have 8-EDO .
- for a constant n and different A1, if d and (Sn/A1) are integers, we have a subset of EDO or EDI (Equal divisions of Interval).
Consider Sn = 1400 , n=8 and A1=70, then we have a subset of a 140-ED (1400.) with Degrees as 7 17 30 46 65 87 112 140 :
- 0.0 70.0 170.0 300.0 460.0 650.0 870.0 1120.0 1400.0
And now for Sn=1400 and n=8,
- If A1=175.0 then we have 8-AID(1400.)
- If A1=56 then we have 700-AID(1400.) with Degrees as 28 73 135 214 310 423 553 700
- If A1=87.5 then we have 112-AID(1400.) with Degrees as 7 16 27 40 55 72 91 112
AID system shows different ascending, descending or linear trend of change in divisions sizes due to relation between n and A1 in AID and EDO with equal degree:
- If choosing A1 greater than division size in equal degree EDO, d is negative and AID is descending.
- If choosing A1 smaller than division size in equal degree EDO, d is positive and AID is ascending.
- If choosing A1 equal to division size in equal degree EDO, d is zero.
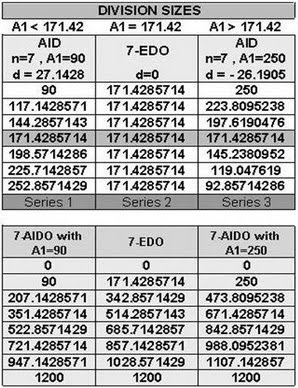
171.4285714 is point of intersection in these 3 trends:
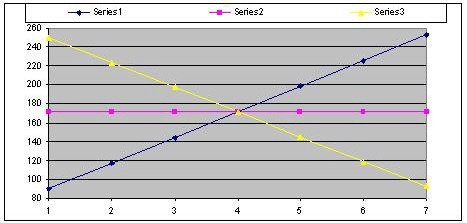
We can have different kinds of AID:
- AIDO = Arithmetic irrational divisions of octave
- AIDINO = Arithmetic irrational divisions of irrational non-octave
- AIDRNO = Arithmetic irrational divisions of rational non-octave
- AIDRI = Arithmetic irrational divisions of rational interval
- AIDII = Arithmetic irrational divisions of irrational interval
Example: Baran scale

