User:VectorGraphics/Periodicity

This page covers a framework for thinking of temperaments and scales in terms of JI lattices, independently derived by User:VectorGraphics, Adriaan Fokker, and likely others.

In terms of temperaments

Lattice of just intervals, with values shown in cents.

Lattice of intervals tempered to schismic temperament. Note that intervals repeat where offset by the location of the schismic comma.

Lattice of intervals tempered to schismic and augmented temperament. Note that this is the same as 12edo, as all intervals are multiples of 100c. Note that no new commas can be added because they would interfere with existing commas.

As an example, we will be working in the 5-limit. Octave-equivalence is assumed, so our lattice has 2 dimensions:

Now, the purpose of doing this is now to look for places where stacking intervals gets you close to zero - that is, commas.

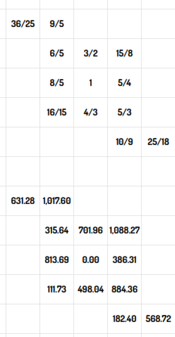
On this table, commas are highlighted with bold text and a darker background color.

There are a lot of possible commas, and choosing one to temper out (say, the interval labelled "1.95", which is the schisma), leads to that comma's temperament. The table of intervals then has zero at the location of that comma, meaning the entire table is periodic.

If one then chooses another comma (say, the interval labelled 41.06 on either chart, which is the augmented comma), the table then becomes periodic both ways, and no new commas can be added (unless, of course, a higher prime is introduced). This table is actually equivalent to a harmonic table of 12edo.

This provides a natural explanation for temperament ranks in regards to comma bases: by adding a comma, it makes the JI lattice repeat on an additional axis (though these may not be directly aligned with the x or y axis), until when there is one less comma than axis, all intervals can be reached by a single generator and period, and when there are as many commas as there are axes, the set of available intervals becomes finite, and the result is an equal temperament.

Such a repeating block is called a "periodicity block", or a "Fokker block", after the mathematician who originally described them, Adriaan Fokker.

From temperaments to scales

A well temperament of 12-edo defined from a Fokker periodicity block, in ratios and in cents. (Both possible mappings of 600c have been provided.)

Such a block can then be placed back into a less restrictive temperament or into just intonation, to define a scale, sort of like a MOS scale but generalized to a higher dimension. For example, one might describe a 12-tone well temperament in 5-limit just intonation by placing a periodicity block representing 12edo into a JI lattice, and seeing what intervals lie within it. This can be treated as a scale on its own (a just chromatic scale), outside of the context of being a 12edo detemper.

In the context of constructing a scale (as opposed to defining a temperament), the intervals chosen at which to repeat the table are called chromas instead of commas, and they define a chroma basis, which tells you which pairs of accidentals you'll need to notate music in that scale. So, for example, our 12-well temperament has the chroma basis {81/80, 128/125}.

A lot of other JI scales (and scales in general, using a tempered lattice) can be constructed as periodicity blocks. For example, the just zarlino scale can be constructed with the chroma basis {81/80, 25/24}. Porcupine temperament equates these two chromas by tempering out the porcupine comma, so the zarlino periodicity block can be placed into a lattice representing porcupine temperament to obtain the porcupine zarlino scale (a MODMOS of porcupine's "Onyx" MOS itself).