Pathology of enfactoring
In this article, we will use lattices to visualize enfactored temperaments, to demonstrate the musical implications of mappings with common factors, and the lack of musical implications of comma bases with common factors.
Defactored case
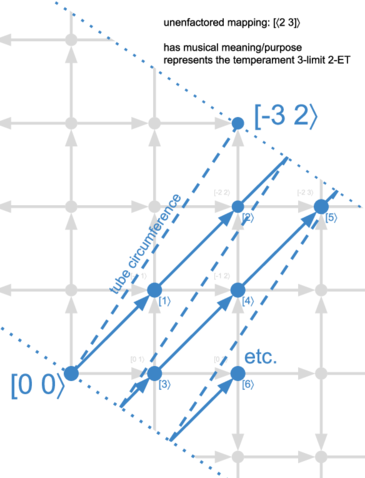
First, let's look at a defactored mapping. This example temperament is so simple that it is not of practical musical interest. It was chosen because it's basically the numerically simplest possible example, where this type of simplicity empowers us to visualize the problem at a practical scale as clearly as possible. Please consider the diagram at right.
This is a representation of 2-ET, a 3-limit, rank-1 (equal) temperament, with mapping [⟨2 3]}, meaning it has a single generator which takes two steps to reach the octave, and three steps to reach the tritave. This temperament makes a single comma vanish, a comma whose vector representation looks similar to the mapping: [-3 2⟩, AKA 9/8. And so the comma basis for this temperament is [[-3 2⟩].
We can imagine that we started out with a JI lattice, where movement up and down correspond to prime 2 (the octave) and movements right and left correspond to prime 3 (the tritave). We have tempered JI here, and so we've faded the JI lattice out to a faint grey color in the background. What we've done specifically is made the comma [-3 2⟩ vanish so that any nodes in this lattice which are 2 over and 3 up from each other are equivalent. Therefore we only need to consider a thin swath of the lattice anymore, specifically, a swath which connects the origin [0 0⟩, AKA 1/1, to [-3 2⟩, and then runs perpendicularly to infinity in either direction.
There's a couple good ways to interpret this situation:
- We've turned on a teleportation field for every point outside this swath, so that it moves by these (-3,2) intervals until it finds its way inside the swath.
- We've rolled up space, so that the line from 1/1 to 9/8 ₋ the width of our swath ₋ is like the circumference of a tube. In this case, since we're only working with 3-limit JI, "space" was only ever 2D, so we can just think of it as paper that we've rolled up, so the pair of dotted lines visualized here are touching along their entire lengths (and if you wanted to imagine further copies of these dotted lines at every (-3,2) interval farther out in either direction, and the paper is infinitely thin, just stack all the dotted lines on top of each other forever).
Either way, then we just superimpose the new tempered lattice on top. It's drawn in blue.
You can see that in the grey lattice underneath, coordinates have 2 values, e.g. [-1 2⟩. That's because the JI lattice essentially had two generators: the octave and the tritave. But tempering has helped us simplify things by reducing us to a single generator, so here, in the new blue-colored tempered lattice, the coordinates have only 1 value, e.g. [8⟩, and they simply indicate how many iterations of the single generator here that we've taken to reach the given point.
We've superimposed the tempered lattice atop the former JI lattice so we can see which JI intervals map to which tempered intervals. For example, [-1 2⟩, AKA 9/2, maps to [8⟩. That tells us that if we want to use the temperament's approximation of the JI interval 9/2, then we want the tempered pitch arrived at by moving by the generator 8 times.
Note that whenever the path the generator takes leaves the main swath, it wraps around to the point on the opposite side. Again, you can think of this either way you prefer: the world is still flat, and you've just warped over there; or, the world has been curled up, and in reality you've been looping back around toward that point the whole time, and the dotted line in this flat representation just represents the point you cut the tube and unrolled it so it could be better visualized on a screen.
The tempered vector for the generator of this temperament is of course [1⟩, but the simplest JI pitch that maps to this generator is [-1 1⟩, or 3/2. It's visually clear why this is the generator. We need to choose an interval which if we repeatedly move by it, while wrapping around the swath, we'll visit every node inside the swath. The best way to do that is to move from the origin to the node that's nearest to the dotted line labelled "tube circumference". We want this node because we want to move away from the tube circumference as little as possible each time, so we avoid skipping any nodes. If it's not obvious, you may want to experiment with drawing the generator line as if it had gone to any other point inside the swath; if you repeated that movement, would you visit every node? No.
All of this so far is actually only just explaining the basic setup for any tempered lattice. But we've got to lay the basics down first in order to discuss the effect of enfactoring. We'll do that now!
Enfactored mapping
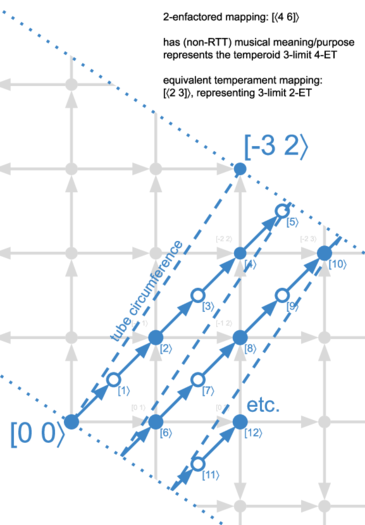
We are now comparing the previous diagram, which had the mapping [⟨2 3]}, with the 2-enfactored version of it, i.e. the mapping 2×[⟨2 3]} = [⟨4 6]}, AKA 4-ET.
If you compare this lattice of an enfactored mapping with the previous lattice for a healthy, defactored mapping, they should look almost the same. They have the same comma and tube circumference. And the generator follows the same path through that tube/swath. The key difference is how far the generator moves with each step along that path.
Starting from the origin, we can see that it takes us 2 moves of the generator to reach the approximation of [-1 1⟩, AKA 3/2, where before we made that step in one go. Then another 2 moves to reach the approximation of [-2 2⟩, AKA 9/4, for a total of 4 moves, where before it only took us 2 steps. As you keep going, you'll see that each node it has taken us 2x as many steps as before to reach it.
And for what? What happens in the steps that are halfway between nodes that were on the JI lattice? These are shown with hollow blue circles instead of filled blue circles, to indicate that there's not JI lattice node underneath them. In other words, while these are legitimate musical intervals, there is no JI interval which would be said to temper to them. In other words, since this is 4-ET, that first generator step is to a node [1⟩ that's about 300¢. But [0 0⟩ tempers to [0⟩ and [-1 1⟩ tempers to [2⟩; nothing tempers to [1⟩. It's an interval that can certainly at least be heard and understood musically, but has no meaning with respect to tempering JI, or in other words, no RTT purpose.
And so this 4-ET doesn't bring anything to the table that isn't already brought by 2-ET. And so it is fitting to consider it only a temperoid, rather than a true temperament. Were this as bad as things got, it might not be worth pushing for distinguishing temperoids from temperaments. But once we look at enfactored comma bases, we'll see why things get pretty pathological.
Enfactored comma bases
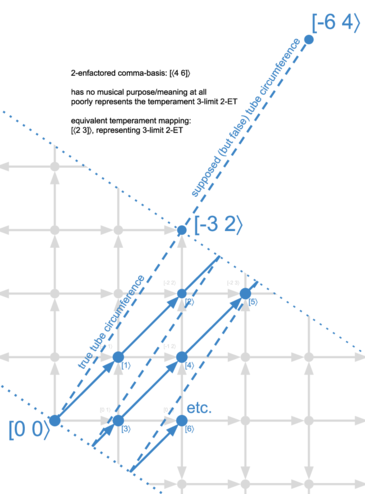
Here's where things get kind of nuts. Most recently we experimented with enfactoring our healthy temperament's mapping. Now let's experiment with enfactoring its comma basis. In the defactored situation, if our comma basis was [[-3 2⟩], then 2-enfactoring it produces 2×[[-3 2⟩] = [[-6 4⟩].
We know that in the original diagram, the large-labelled [-3 2⟩ represented our comma, and this was the point that our dotted line ran through, the one that represented our boundary of warp/wrap. So our first thought should be: we must alter our diagram so that now [-6 4⟩ is that point instead. Fine.
But here's the problem. It simply doesn't make sense to double the width of our swath/tube! If [-6 4⟩ is made to vanish, then so is [-3 2⟩. That is, while nothing would stop you from drawing a diagram with a double-width swath/tube, the musical reality is that it is impossible to make [-6 4⟩ vanish without also making [-3 2⟩ vanish. And so there is no meaning or purpose to the comma basis [-6 4⟩, whether RTT-wise or musically in general. It is garbage.
And so our lattice for an enfactored comma basis looks almost identical to the original defactored lattice. The only difference here is that we've drawn a "supposed (but false)" tube circumference out to [-6 4⟩, while the half of this length which is real is now labelled the "true" circumference.
Enfactored comma bases vs. periodicity blocks with torsion
And now we're prepared to confront the key difference between the enfactored comma basis of a temperament, and torsion of a periodicity block.
What they have in common is that both take the form of a common factor found somewhere in linear combinations of entries in a list of commas defining a pitch structure, and that these commas can be visualized by slicing the JI lattice into swaths of "periodicity" (that's just a fancy word for the effect we've already been observing for temperaments, where nodes outside the swath related by the size of that comma are considered equivalent and therefore redundant, or repetitions of the same pitch class).
The key difference is that the former (temperaments) tempers the commas out, while the latter (periodicity blocks) does not.
Why is this the key difference? Well, remember how in the previous section, the reason we couldn't actually extend the width of the swath/tube to [-6 4⟩ was because the tempering: if [-6 4⟩ is made to vanish, then [-3 2⟩ is as well, so the swath/tube cannot legitimately be extended. Since there is no tempering in the case of periodicity blocks, however, the width can legitimately be extended in this way.
Let's take a look at the example given in Tonalsoft's page for torsion. The diagram there has been reworked here to help clarify things. The origin, 1/1, has been placed in the corner of this parallelogram-shaped block, and the two commas that define it are in two of the other corners: 2048/2025 and 625/324. The value at the fourth corner, 12800/6561, has vector 2×[-8 8 -2⟩. The first 2 is just to octave-reduce it to being positive, but you may recognize the actual vector part as 2 times the meantone comma. The most important part is that the vector is 2-enfactored. You can see that the node at the very center of this block is 160/81, which again is 2×[-4 4 -1⟩, or the octave-reduced non-enfactored version of that same comma.
The red and blue lines that wrap around this block are two different generator paths. The point here is to show that by doubling the size of this periodicity block, we have made it impossible to choose a node to travel to from the origin, i.e. a generator, such that you can reach every node in the block. Instead, the best you can do is reach half of the nodes; that's the red path from the origin 1/1. The blue path is an exact copy of the red path, but offset.
So we can see how tempting the duality can be here. In the case of a 2-enfactored mapping, the generator path reaches twice as many nodes as there were JI nodes. But in the case of a 2-enfactored comma basis — if we could legitimately extend the width of the block, as we do in untempered periodicity blocks! — we would reach half as many nodes. But this duality just is not musically, audibly real.
Enfactored mappings vs. enfactored comma bases
One may pose the question: what is the relationship between an enfactored mapping and an enfactored comma basis? Can you have one but not the other? Must you? Or must you not? Or does the question even make sense? Certainly at least some have suggested these cases are meaningfully independent[1].
The conclusion we arrive at here is that because enfactored comma bases don't make any sense, or at least don't represent any legitimately new musical information of any kind that their defactored version doesn't already represent, it is not generally useful to think of enfactored mappings and enfactored comma bases as independent phenomena. It only makes sense to speak of enfactored temperaments. Of course, one will often use the term "enfactored mapping" because enfactored mappings are the kind which do have some musical purpose, and often the enfactored mapping will be being used to represent the enfactored temperament — or temperoid, that is.
Footnotes
- ↑ such as the page color notation, which reads "it's possible that there is both torsion and contorsion"