User:R-4981/Redbull
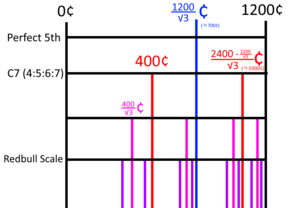
The Redbull scale[idiosyncratic term] is a 16-tone logarithmic fractal scale obtained by recursively dividing one octave on the logarithmic scale (1200 ¢) with a 1:√3 ratio.
Theory
400 ¢ is the most commonly used approximation to 5/4, mainly due to its use in 12edo. This interval is also expressed as 1\3, and its square root on the logarithmic scale, ≈692.82 ¢ (hereinafter expressed as 1\√3 for convenience), functions as an approximation of 3/2. (The comma between these two intervals is called as Caffeinterval.) Furthermore, the interval divided into √3 equal parts with 1\√3 as the center[clarification needed] is ≈985.641¢, which works as an approximation of 7/4 or 9/5, and the tetrad that combines these is 4:5:6:7, the so-called It will be the C7. Applying this property, the scale that is created as a result of recursively dividing those intervals furthermore twice is Redbull.
Most of the notes on this scale are irrational numbers in both cent and frequency units, so Redbull cannot be reproduced with an edo. Also, since there is no interval that can be called a generator, it is also impossible to approximate Redbull with a mos scale. Also, since there is no interval that can be called a generator, and it varies even by one step[clarification needed], there are many intervals within Redbull that approximate just intonation, just like afdos.
Intervals
For more precise cent values, refer to the Scala file below.
| Degree | Cents | Approximate ratios |
|---|---|---|
| 0 | 0 | 1/1 |
| 1 | 133.333 | 14/13, 13/12, 12/11 |
| 2 | 230.940 | 8/7, 9/8 |
| 3 | 328.547 | 6/5 |
| 4 | 400 | 5/4, 24/19 |
| 5 | 497.607 | 4/3 |
| 6 | 569.060 | 25/18, 7/5, 11/8 |
| 7 | 640.513 | 10/7, 13/9, 16/11 |
| 8 | 692.820 | 3/2 |
| 9 | 790.427 | 11/7 |
| 10 | 861.880 | 13/8, 18/11, 5/3 |
| 11 | 933.333 | 12/7 |
| 12 | 985.641 | 7/4, 9/5 |
| 13 | 1057.094 | 11/6, 24/13, 13/7 |
| 14 | 1109.401 | 15/8, 17/9, 28/15 |
| 15 | 1161.708 | 33/17, 64/33 |
| 16 | 1200 | 2/1 |
Properties and trivia
- As mentioned above, the tetrad obtained by stacking 4-steps from the tonic (i.e. starting on degree 0) is similar to the seventh tetrad in 12edo, approximating 4:5:6:7. Since 4 is a divisor of 16, there are only 4 types of 4-step tetrads, the others being only inversions, and the other types of 4-step tetrads do not approximate 4:5:6:7. (in example, chords stacked 4 steps from 2 steps above the tonic is approximating 9:11:13:17.)
- The pentad obtained by stacking 3-steps from the tonic approximates 5:6:7:8:9.
- Furthermore, Redbull has a pentatonic subset which is similar to 2L 3s[clarification needed], and the constituent notes of that scale can be approximated as 9:12:13:16:17 in just intonation.
- The name Redbull, proposed by R-4981, comes from the energy drink brand from Austria.
Scala file
! redbull.scl ! 16-tone logarithmic fractal scale with 1:√3 16 ! 133.33333333 230.94010768 328.54688202 400. 497.60677434 569.05989232 640.51301031 692.82032303 790.42709737 861.88021535 933.33333333 985.64064606 1057.09376404 1109.40107676 1161.70838948 1200.