Prime harmonic series
The acoustic prime harmonic series is similar to the set of prime numbers, except that it begins with 1, and skips 2 because of octave equivalence : 1, 3, 5, 7, 11, 13 etc.
If “new” pitch classes in the harmonic series are always odd numbers (even numbers are always octave duplications), the question is whether there is a useful acoustic/musical distinction between odd composites and primes. The test case is 9, which is the first odd numbered partial that is composite.
Suppose one is producing notes with harmonic spectra whose fundamentals are members of an harmonic series. Each note that is played also exhibits its own series of partials as its timbre. Some of these partials may coincide with member of the original harmonic series. For example, a note whose fundamental is the 3rd member of an harmonic series will have its own third partial coincident with the 9th partial of the original series. (9 = 3 × 3). It can be shown that all further odd composite members of the original series will show up in the spectra of notes built on lower partials (e.g. 15 = 5 × 3 = 3 × 5). On the other hand, prime numbered partials of the original series do not occur in notes built on lower partials. So, do composites exhibit a kind of redundancy? Does this result in some kind of qualitative/musical difference between primes and composites, and the notes built upon them? Is the derivative nature of the composite members audible? These are questions which may lie in the realm of subjectivity, but one thing is certain: 7 and 11 sound more unusual to our ears than 9 does. If odd limit as a measure of consonance was all that mattered, wouldn’t there be a continuum of some kind from 7 to 9 to 11? Instead, 9 sounds like it belongs with its 3-limit brothers 3/2 and 4/3 far more than it does with 7 or 11.
Fortunately, it is not necessary to wait upon the answers to these admittedly very interesting questions before finding interesting uses for the prime harmonic series as material for scale generation. For example, through the magic of octave reduction, the first n members of the prime harmonic series can produce an n-atonic scale:
| N (primes) | scale |
| 1 (1) | 1/1 |
| 2 (1,3) | 1/1, 3/2 |
| 3 (1,3,5) | 1/1, 5/4, 3/2 |
| 4 (1,3,5,7) | 1/1, 5/4, 3/2, 7/4 |
| 5 (1,3,5,7,11) | 1/1, 5/4, 11/8, 3/2, 7/4 (pentatonic) |
| 6 (1,3,5,7,11,13) | 1/1, 5/4, 11/8, 3/2, 13/8, 7/4 (hexatonic) |
| 7 (1,3,5,7,11,13,17) | 1/1, 17/16, 5/4, 11/8, 3/2, 13/8, 7/4 (heptatonic) |
| 8 (1,3,5,7,11,13,17,19) | 1/1, 17/16, 19/16, 5/4, 11/8, 3/2, 13/8, 7/4 (octatonic) |
| 9 (1,3,5,7,11,13,17,19,23) | 1/1, 17/16, 19/16, 5/4, 11/8, 23/16, 3/2, 13/8, 7/4 (nonotonic) |
| 10 (1,3,5,7,11,13,17,19,23,29) | 1/1, 17/16, 19/16, 5/4, 11/8, 23/16, 3/2, 13/8, 7/4, 29/16 (decatonic) |
| 11 (1,3,5,7,11,13,17,19,23,29,31) | 1/1, 17/16, 19/16, 5/4, 11/8, 23/16, 3/2, 13/8, 7/4, 29/16, 31/16 (hendecatonic) |
| 12 (1,3,5,7,11,13,17,19,23,29,31,37) | 1/1, 17/16, 37/32, 19/16, 5/4, 11/8, 23/16, 3/2, 13/8, 7/4, 29/16, 31/16 (dodecatonic) |
Of course, as in scales derived from the full series, there is nothing that says one must start at the beginning of the series or include consecutive members only. The possibilities are endless.
The prime heptatonic scale can be notated like this:
16:17:20:22:24:26:28:(32)
giving the following step sizes:
| 17/16 | 20/17 | 22/20 (11/10) |
24/22 (12/11) |
26/24 (13/12) |
28/26 (14/13) |
32/28 (8/7) |
| 104.96 | 281.36 | 165 | 150.64 | 138.57 | 128.3 | 231.17 |
The prime dodecatonic scale can be notated:
32:34:37:38:40:44:46:48:52:56:58:62:(64)
giving these step sizes:
| 34/32 (17/16) |
37/34 | 38/37 | 40/38 (20/19) |
44/40 (11/10) |
46/44 (23/22) |
48/46 (24/23) |
52/48 (13/12) |
56/52 (14/13) |
58/56 (29/28) |
62/58 (31/29) |
64/62 (32/31) |
| 104.96 | 146.39 | 46.17 | 88.8 | 165 | 76.96 | 73.68 | 138.57 | 128.3 | 60.75 | 115.46 | 54.97 |
Any segment of the prime harmonic series can be used "as is" as musical material.
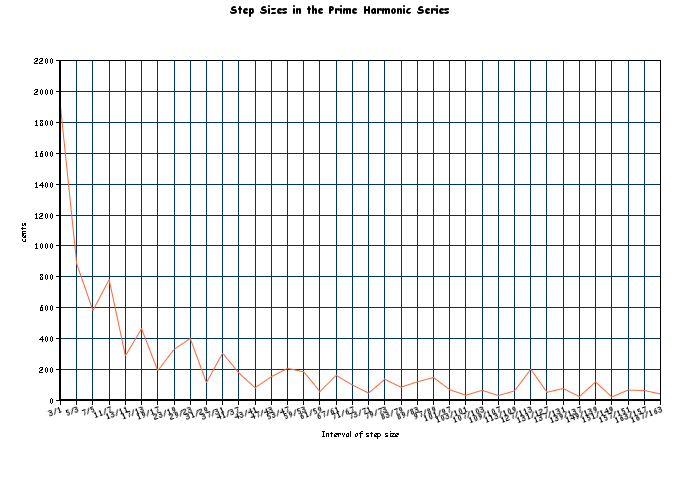
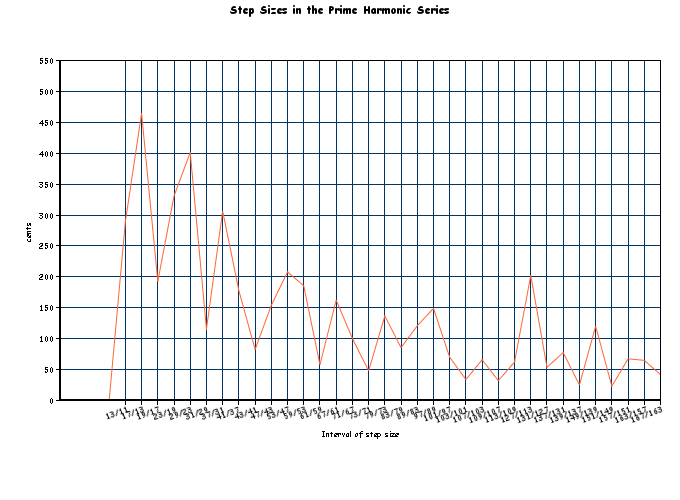
The step sizes of the series itself exhibit an interesting variety, including the phenomena of twin primes which provide for small steps which contrast with the wider steps elsewhere in the series:
a closer look at the steps above 11:
One example of using the prime harmonic series as a "found object" is Dante Rosati's "prime guitar".
Dante writes:
"The Prime Guitar is designed to play prime partials 17-199. The lowest string is tuned to the 17th partial of a series, and the successive strings are then tuned to partials 23, 37, 47, 67, and 89 to preserve the basic tonal spread of a standard set of guitar strings. Since every single note is a unique prime limit pitch, it was not practical to color code the frets in the same way as the previous guitars. On the other hand, it is very difficult to orient one's self on a neck with such irregular fret spacing without any color coding, so I settled on a simple alternating three color scheme that allows for easy visual spotting of where the frets are located.
Because the lowest partial is 17, there are no familiar lower prime limit intervals like octaves (2/1), fifths (3/2), thirds (5/4), etc. Nevertheless, some intervals between higher primes approximate the lower prime limit intervals (e.g. 61/31 is very close to an octave), without of course reproducing them exactly." (original page source)
"Tarkovsky's Mirror" for prime guitar by Dante Rosati
| prime harmonic | cents (octave reduced) | sorted | delta |
| 2 | 0 | 0 | 104.9554095 |
| 3 | 701.9550009 | 104.9554095 | 146.3886293 |
| 5 | 386.3137139 | 251.3440388 | 46.16897738 |
| 7 | 968.8259065 | 297.5130161 | 88.80069773 |
| 11 | 551.3179424 | 386.3137139 | 42.74869168 |
| 13 | 840.5276618 | 429.0624055 | 82.4553001 |
| 17 | 104.9554095 | 511.5177056 | 39.80023672 |
| 19 | 297.5130161 | 551.3179424 | 76.9564049 |
| 23 | 628.2743473 | 628.2743473 | 37.23227474 |
| 29 | 1029.577194 | 665.506622 | 36.44837885 |
| 31 | 1145.035572 | 701.9550009 | 138.5726609 |
| 37 | 251.3440388 | 840.5276618 | 32.97688371 |
| 41 | 429.0624055 | 873.5045455 | 95.32136099 |
| 43 | 511.5177056 | 968.8259065 | 60.75128768 |
| 47 | 665.506622 | 1029.577194 | 29.59446508 |
| 53 | 873.5045455 | 1059.171659 | 57.71314584 |
| 59 | 1059.171659 | 1116.884805 | 28.15076739 |
| 61 | 1116.884805 | 1145.035572 | 54.964428 |