Latitude
Latitude is a measure of an interval's size in relation to a (possibly tempered) fifth, or another interval (the "axis of polarity" or just "axis") serving the same function in another harmonic system. An interval as defined by its latitude may be called a "medial" and always has an axis complement. Latitude ranges from 90 degrees Minor (-90°) to 90 degrees Major (90°), corresponding to 180edA where A is the axis. "Low-latitude" means close to 0 degrees, "high-latitude" means close to ±90 degrees.
Latitude allows the characterization of, i.e. different "flavors" of thirds, with respect to a fifth that might be tempered, as opposed to in terms of absolute interval ranges that may be misaligned with the intervals' harmonic function. For example, one might describe 3\13, 4\13, and 5\13 in 13edo based on their size as a subminor third, a submajor third, and an ultramajor third, but that doesn't reflect their function in triadic harmony in 13edo. Using latitude, one can see that their latitudes are -22.5°, 0°, and 22.5°, and from that they may be assigned the labels subminor, neutral, and supermajor, which better reflect their role.
They additionally allow the generalization of the triadic concept to "axis" intervals other than the fifth. For example, if one were to make a harmonic system using 5/3 as the "axis" rather than 3/2, chords built within a range of 5/3 would contain 3:4:5 and 12:15:20, and the medial intervals of the major third and perfect fourth would have a latitude of ±11.4°
Medial pairs with a higher latitude than ±45° tend to sound more dissonant against the axis or root than lower-latitude medials, and extremely low-latitude interval pairs may not sound distinct from each other. Higher latitude enables "cross-tonality", where both intervals in the pair can be played at once in the same chord, as in suspended or arto/tendo chords.

Here is a table of the latitude of medials up to ±30° in various EDOs, with respect to their fifth as the axis:
| Fifth size in edosteps | Edos | Latitude (±n°) |
|---|---|---|
| 3 | 5 | 30 |
| 4 | 7 | 0 |
| 5 | 9 | 18 |
| 6 | 10 | 0, 30 |
| 7 | 12 | 12.8 |
| 8 | 13, 14 | 0, 22.5 |
| 9 | 15, 16 | 10, 30 |
| 10 | 17, 18 | 0, 18 |
| 11 | 18, 19 | 8.2, 24.5 |
| 13 | 22, 23 | 6.9, 20.8 |
| 14 | 23, 24, 25 | 0, 12.8, 25.7 |
| 15 | 25, 26, 27 | 6, 18, 30 |
| 16 | 26, 27, 28 | 0, 11.3, 22.5 |
| 17 | 28, 29, 30 | 5.3, 15.9, 26.5 |
| 18 | 30, 31, 32 | 0, 10, 20, 30 |
| 20 | 33, 34, 35, 36 | 0, 9, 18, 27 |
| 24 | 39, 40, 41, 42, 43 | 0, 7.5, 15, 22.5, 30 |
| 31 | 51, 52, 53, 54, 55, 56 | 2.9, 8.7, 14.5, 20.3, 26.1 |
Latitude-based interval regions
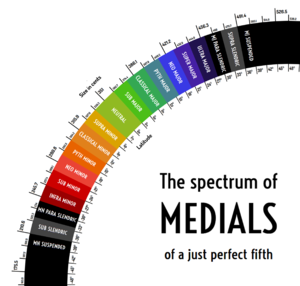
Names can be given to intervals based on latitude. A table is provided here for fifths:
| Latitude | Major name | Minor name | General name | Type |
|---|---|---|---|---|
| ±0 to 3° | (Tendo)-neutral third | (Arto)-neutral third | Neutral thirds | Third |
| ±3 to 7° | Submajor third | Supraminor third | Intraclassical thirds | |
| ±7 to 12° | Classical major third | Classical minor third | Classical thirds | |
| ±12 to 16° | Pythagorean major third | Pythagorean minor third | Pythagorean thirds | |
| ±16 to 20° | Neogothic major third | Neogothic minor third | Neogothic thirds | |
| ±20 to 24° | Septimal major third, supermajor third | Septimal minor third, subminor third | Septimal thirds | |
| ±24 to 28° | Tendo third, ultramajor third | Arto third, inframinor third | Tridecimal thirds/interseptimals | |
| ±28 to 32° | Major paraslendric | Minor paraslendric | Paraslendrics | Second/fourth |
| ±32 to 36° | Supraslendric | Subslendric | Extraslendrics | |
| ±36 to 40° | Major suspended | Minor suspended | Suspendeds | |
| ±40 to 44° | Suprasuspended | Subsuspended | Extrasuspendeds | |
| ±44 to 48° | Major paratetracot | Minor paratetracot | Paratetracots | |
| Beyond ±48° | - | |||
Diatonic and antidiatonic fifths can also be categorized by the latitude of the medials they generate:
| Third type | Category | Tuning range | EDO |
| Interseptimal | Inframedio | 654.6-660.5 | 11edo |
| Septimal | Avila | 660.5-664.6 | 29edo |
| Neogothic | Pelogic | 664.6-668.7 | 9edo |
| Pythagorean | Mediocratic | 668.7-672.9 | 25edo |
| Classical | Mavila | 672.9-678.2 | 16edo |
| Intraclassical | Sharpmavila | 678.2-682.5 | 30edo |
| Neutral | Neutral | 682.5-689 | 7edo |
| Intraclassical | Flattone | 689-693.4 | 26edo |
| Classical | Meantone | 693.4-699 | 19edo |
| Pythagorean | Pythagorean | 699-703.6 | 12edo |
| Neogothic | Neogothic | 703.6-708.2 | 17edo |
| Septimal | Archy | 708.2-712.8 | 22edo |
| Interseptimal | Ultrapyth | 712.8-720 | 5edo |
Triads
Just triads containing arithmetically progressed frequency divisions - that is, isoharmonic triads - are always "major"; how major it is can be characterized by latitude.
| Name | Triad | Latitude of medial |
|---|---|---|
| 1:3:5 | 32.8° | |
| 1:2:3 | 23.5° | |
| BP "wide" triad | 3:5:7 | 18.5° |
| 2:3:4 | 15.3° | |
| BP "narrow" triad | 5:7:9 | 13° |
| Inverted major triad | 3:4:5 | 11.4° |
| Mintaka triad | 7:9:11 | 10.1° |
| Major triad | 4:5:6 | 9.1° |
| 9:11:13 | 8.2° | |
| (Septimal) diminished triad | 5:6:7 | 7.5° |
| 11:13:15 | 7° | |
| Quartal triad | 6:7:8 | 6.5° |
| 13:15:17 | 6° | |
| 7:8:9 | 5.6° | |
| 15:17:19 | 5.3° | |
| 8:9:10 | 5° |