MOS diagrams
The moment-of-symmetry process of unfolding a scale takes, for most people, a conceptual leap or two. Below are visualizations of the process:
- From the Wilson Archives on Kraig Grady's Anaphoria.com:
- The first set of 32 horograms – see also Horogram.
- The Scale Tree is the basis of the horograms.
- Moments of Symmetry, of Equal Divisions of the Octave.
- From David Finnamore's Elevenminstrel.com: 5- To 9-Tone, Octave-Repeating Scales From Wilson's Golden Horagrams of the Scale Tree.
- Charles Lucy describes a technique involving dis-continuous chains of fifths (i.e. skipping some).
- Joseph Monzo's helixes could also be of use here...
- User:Xenoindex's charts User:Xenoindex/MOS_Charts
L and s
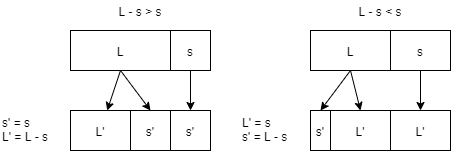
The mechanics of scale generation are such that—when iterating from one scale to the next densest one—all large steps in the preceding scale become one large step and one small step in the new scale.
Another way to think about this is that a small-step-sized chunk has been split off of each of the former large steps. The remainder can be either larger or smaller than the small step
- If it is larger, then it stays the large step.
- If it is smaller, then it becomes the new small step, and everything that used to be a small step is now a large step.
We are reasoning about MOS concepts in the abstract here. These truths about large and small steps are true whether they are 100¢ or 4516.8¢, and all we really care about are their ratios. So if we treat our small steps’ size as [math]1[/math] then we can treat our large steps’ size as equal to the [math]L{:}s[/math] ratio.
So the [math]L{:}s[/math] ratio decreases by [math]1[/math] because if an [math]s[/math]-sized chunk has been sliced off [math]L[/math], and [math]s[/math]’s size is [math]1[/math], then [math]1[/math] should be subtracted from [math]L[/math].
When [math]L - s \gt s[/math]:
[math] \begin{align} L’{:}s’ &= (L - s){:}s \\ &= (L - 1){:}1 \\ &= L - 1 \end{align} [/math]
When [math]L - s \lt s[/math], the result is simply reciprocated:
[math] \begin{align} L’{:}s’ &= s{:}(L - s) \\ &= 1{:}(L - 1) \\ &= \frac{1}{L - 1} \end{align} [/math]