How to make a Kite Guitar
This page covers all options from simple DIY conversions to custom builds by professional luthiers.
General design considerations
Converting an existing guitar vs. building a new one
Converting is far more affordable than building, and is the main focus here. If building, there are only a few differences from building a standard guitar:
- more frets, obviously
- the number of strings, and hence the total tension on the neck
- the string gauges, and hence the size of the nut slots
- the process for intonating the saddle points
- because open strings are used less, a zero fret is more feasible
Even-frets vs. odd-frets
There are two types of Kite Guitar fretboards, even-frets and odd-frets. In the former, all or almost all of the frets are an even number of 41-equal steps from the nut. In the latter, it's an odd number. The even-frets layout is primarily for isomorphic ("same-shape") tunings and the odd-frets layout is primarily for open tunings. Most of the research and development to date has focused on the even-frets layout.
In-between frets
An odd-frets guitar can be converted to an even-frets one simply by capoing. An even-frets one can be converted to odd-frets similarly if there is an additional fret (or fret slot that accepts a temporary fret) near the nut. There are also advantages musically to this extra fret even if not using open tunings. The extra fret or "in between" fret is named the "a-fret" if it's between the nut and the 1st fret, "b-fret" if it's between the 1st and 2nd frets, etc. (An alternative terminology is 0.5-fret, 1.5-fret, etc.) A b-fret or b-fret-slot might be better for acoustics, which tend to have higher nuts, which might make capoing only 29¢ from the nut difficult. An empty fret slot does not interfere at all with normal play. Thus there is absolutely no downside to having an a-slot and/or a b-slot, and it's highly recommended.
On a Kite guitar, each string fills in the missing notes on the neighboring strings. But there are 6 missing notes in the very upper and lower ranges. The 6 gaps in the upper range are fairly easily filled with half-fret bends. To fill the 6 low gaps, one might want short "fretlets" on the lowest string, especially on a bass guitar. Their names run from a-fretlet to f-fretlet.
Scale length and number of strings
Arguably a slightly longer scale, say 26.5-27", is nice because it makes the frets less cramped. Fortunately 7- and 8-string electric guitars often have longer scales anyway. But on the other hand, the Kite guitar's frets are not much tighter than a normal mandolin's, and some feel a longer scale isn't necessary.
Assuming one is not using an open tuning, a Kite guitar with 6 strings is a little limiting. 7 strings or even 8 is better.
Converting a 6-string or 12-string to a 7-string
While 7- and 8-string electric guitars are plentiful, acoustic ones are rarer. (See Extended range guitar.) One way to get one is to convert a 12-string guitar. The neck will be sufficiently strong and there will be enough tuners (aka tuning machines or machine heads). On the bridge, fill in all but the outer two pin holes. Then measure the distance between these two holes, divide by 6, and draw 5 new lines. (For an 8-string, divide by 7 and draw 6 new lines.) Drill new pin holes accordingly. There's fewer strings but more courses, so the string spacing can be very tight. To avoid this, the new fretboard can be wider than the old one. The fretboard overhang can be filled with bondo to create a nice-feeling neck.
Another possibility is to convert a 6-string classical nylon-string to 7 or 8 strings. The tension is low enough that an extra string or two won't break the guitar. The fingerboard is wide enough that it may suffice as is. If not, again the new fretboard can be slightly wider.
To add an additional tuner or two, the 3 holes on each side of the headstock that the tuner pegs go through can be filled and 4 new holes drilled. Or a ukulele tuner or two can be added at the top of the headstock. (Banjo tuners can work too.) Use the type of tuner that has the knob pointing backwards, not sideways (i.e. perpendicular to the headstock, not parallel to it). For ease of use, get one that is geared (via a planetary gear), so that many turns of the knob equals one turn of the post that the string passes through. This set of 4 ukulele tuners from graphtech.com is $33 plus shipping.
There will need to be new 1/16" holes in the tie block. One could drill at an angle, entering from near the upper edge of the back of the tie block. But it's better to go straight in with an extra-long bit, perhaps 6" long. Or you can use a bit extension. This type is good because it's magnetic so there's no chuck to get in the way: harborfreight.com/6-in-magnetic-hex-bit-extension-62691.html. Make sure the bit is long enough to pass through both the guide block and the tie block. This one should be long enough: harborfreight.com/titanium-hex-shank-drill-bit-set-13-piece-61621.html.
On the tie block, divide the distance between the outer holes by 6 and draw 5 lines for your 5 new holes (or for an 8-string, divide by 7 and draw 6 lines). Fill the inner 4 holes with toothpicks. You can thin the toothpick down by putting it in a drill press (or even a hand drill) where the bit would go. Then run a bit of sandpaper against it as it spins. Squirt some runny superglue on it and shove it into the hole. Cut off the excess with a razor blade. Squirt a bit more superglue onto the exposed end.
To help get the precise angle and spacing, make a guide block out of a hard material like maple wood or delrin. Use a drill press to drill a 1/16" hole in it that is at the right height and angle. Draw a guide line on the top for aligning.
If you don't like tying knots when you change strings, you can take this opportunity to drill 2 or even 3 holes per string. Look up "12-hole tie block" and "18-hole tie block" for details. Drill an extra hole or two into your guide block at the proper distance.
Position the block right up against the tie block and use the guide line to align it with one of the lines you drew on the top of the tie block. Use two-sided tape on the bottom of the block to hold it in place. To protect the face of the guitar, take a thin metal plate and cover the edges with tape. Then tape it to the guitar face.
Drill the hole(s) for this string with a 1/16" drill bit. Drill a little at a time and clean the dust off the bit between passes. Leave the metal plate in place and reposition the guide block to drill the remaining holes.
The nut will need to be replaced. Making a high-quality nut is a bit tricky for the amateur DIY-er, and you may need to use a luthier. But if the new fretboard has a zero fret, the nut merely serves as a spacer. It doesn't affect the sound, and the exact width and depth of the nut slots don't matter as much. Because both the nut and the tie block holes will be replaced, and because the new fretboard can be a little wider or narrower than the old one, one has a lot of control over the new string spacing.
Range
The range affects the string gauges, which should match the nut slots. The string gauges also affect the saddle compensation. So ideally the range is chosen before conversion or construction. In the table below, the less likely ranges are in parentheses.
| range | notes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| guitar | full-8 | vD | ^^F | ^A | C# | F | vA | ^^C | ^E | |
| high-7 | ^^F | ^A | C# | F | vA | ^^C | ^E | |||
| low-7 | vD | ^^F | ^A | C# | F | vA | ^^C | |||
| (high-6) | ^A | C# | F | vA | ^^C | ^E | ||||
| mid-6 | ^^F | ^A | C# | F | vA | ^^C | ||||
| (low-6) | vD | ^^F | ^A | C# | F | vA | ||||
| deep-8 | Bb | vD | ^^F | ^A | C# | F | vA | ^^C | ||
| deep-7 | Bb | vD | ^^F | ^A | C# | F | vA | |||
| bass | full-6 | vD | ^^F | ^A | C# | F | vA | |||
| (high-5) | ^^F | ^A | C# | F | vA | |||||
| low-5 | vD | ^^F | ^A | C# | F | |||||
| (high-4) | ^A | C# | F | vA | ||||||
| mid-4 | ^^F | ^A | C# | F | ||||||
| low-4 | vD | ^^F | ^A | C# | ||||||
| deep-7 | Bb | vD | ^^F | ^A | C# | F | vA | |||
| deep-6 | Bb | vD | ^^F | ^A | C# | F | ||||
| (deep-5) | Bb | vD | ^^F | ^A | C# | |||||
Nut width
This is a crucial decision when there are 7 or 8 strings, as too wide a nut is hard on the wrist, but too narrow a nut makes fretting cleanly difficult. Nylon strings need a wider nut not only because the strings themselves are wider, but also because they vibrate more widely than steel strings and need more room. See the String Spacing section below. See also Extended range guitar#Nut and saddle widths and guitarplayerhq.com/7-string-guitar-nut-width.
Number of frets
The following discussion does not include any "in between" frets, e.g. a-fret, b-fret, etc.
In any given key, the Kite guitar has multiple "rainbow zones" on the neck. Assuming the tonic falls in the "sweet spot" between the 4th and 11th fret, it takes about 28 frets to provide 2 zones in every key, but it takes the full 41 frets to provide 3 zones. This 3rd zone increases the range the lead guitarist has to solo in by a 5th or so. The highest frets are very tight, but still playable melodically. Chording is very difficult. Having a 41st fret makes intonating the guitar easier, see Saddle and Nut Compensation below. In general, if you can fit in 41 frets, do so.
There is a 'home zone" around the 14th fret that is the rainbow zone when the low open string is the tonic. There is a 2nd home zone around the 28th fret. To get a complete 2nd home zone, one needs about 32 frets. This should be the minimum number of frets even on an acoustic or classical without a cutaway. Fortunately this translates to almost 19 conventional frets, which almost all guitars have.
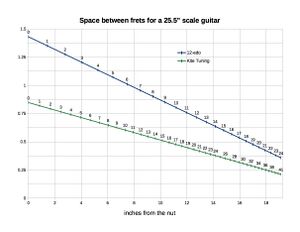
The fret spacing is 1.71 times tighter than a 12-equal guitar. This chart compares it to the standard fret spacing. The spacing between the nut and the first fret is about the same as the space between the 12-equal 9th and 10th frets. Increasing the overall scale length will widen the spacing.
Choosing the right fret wire
The frets should be as narrow as possible, because the frets are so closely spaced high up on the neck. One can always manage to produce the desired note, even with wide frets closely packed. But to get good sustain, it helps to get one's finger behind the fret, so that the fleshy fingertip doesn't overhang the fret and deaden the note. The narrower the fretwire, the easier that is.
If the fretwire is somewhat tall, that aids microbending to sharpen the downmajor 3rds, because one can simply squeeze those notes harder. Taller frets also prolong the life of the frets, since repeated fret leveling over the years wears them down.
Two possibilities are Jescar FW50078 (.078X.050) and Stew-Mac Medium/Highest #0155 (.080x.050).
Replacing each fret vs. replacing the entire fretboard
When converting a guitar, it's best to replace the entire fretboard, rather than removing the frets and putting new frets in the old fretboard. Here's why: the 41-equal 5th is 702.5¢, so two frets will be only 2.5¢ away from the old 12-equal frets, two will be 5¢ away, etc. So the old and new fret slots overlap, making conversion difficult. The following table shows the distance from the old fret to the new fret for close pairs. One could just use the old slots (or even the old frets) and accept a few cents error. But in certain keys a 5¢ error will make the downmajor 6th or 10th that's already 6¢ flat a full 11¢ flat.
| old fret | 7 | 10 | 14 | 17 | 20 | 21 |
|---|---|---|---|---|---|---|
| new fret | 12 | 17 | 24 | 29 | 34 | 36 |
| cents | 2.5¢ | -5¢ | 5¢ | -2.5¢ | -10¢ | 7.5¢ |
| distance | 0.024" | -0.040" | 0.032" | -0.013" | -0.045" | 0.032" |
Removing the entire fretboard also has the advantage that you can get a pre-slotted computer-cut fretboard fairly cheaply that has extremely accurate slot placement (see Fret Placement below).
Fret placement
On a standard guitar, the nth fret is SL * (1 - 2^(-n/12)) from the nut, where SL is the scale length. On a Kite guitar, for an even-fret layout, it's SL * (1 - 4^(-n/41)). In other words, simply replace the 12th root of 2 with the 41st root of 4. For the a-fret, use n = 0.5. The b-fret is 1.5, the c-fret is 2.5, etc. Or use this LibreOffice spreadsheet:
KiteGuitarFret&DotPlacementCalculator.ods.zip
The spreadsheet also has formulas to locate the fret markers aka dots (see the next section).
Various suppliers can make pre-slotted fingerboards complete with radius, taper and inlays. All you need to do is glue it on and put in the frets. All of these suppliers have made Kite guitar fretboards:
- KOZM Guitars (Oregon)
- Starrett Guitars (Colorado)
- JLJ Instruments (Maryland)
- Tonedevil Guitars (Idaho)
- Precision Pearl (Texas)
Adding in-between frets or fretlets
This section covers adding new frets or fretlets (short frets that don't reach all the strings) to an already completed Kite guitar. The fret you are adding may or may not have a tang, and you may or may not need to cut a fret slot for it. A tangless fret is secured with glue or two-sided tape. You can place it temporarily with ordinary tape over the top of it, and check the cents with a tuner. Then mark the position with a pencil and attach it more permanently with superglue. Or you can find the correct position using the following formulas.
To add tangless frets, measure X and F (or X+F and F) like so:
The new fret will not be exactly equidistant from the neighboring frets. It will be slightly closer to the higher one. The formulas are:
- D1 = (X + F) / (1/K + 1) - F/2 (edge-to-edge distance from the lower fret to the new fret)
- D2 = (X + F) / (K + 1) - F/2 (edge-to-edge distance from the new fret to the higher fret)
- K = 41st root of 2 = 2 ^ (1/41) = 1.017049
- 1/K + 1 = 1.983 (mnemonic: 1983 A Merman I Should Turn to Be)
- K + 1 = 2.017
K is a constant for all Kite guitars. F is constant for a specific Kite guitar and the specific fretwire used for the new frets. (These formulas work even if the original frets and the new frets are different widths.) X varies for each fret.
Use either D1 or D2, or both, to place the fret.
If one is instead cutting a fret-slot for a fret with a tang, D1 and D2 are the distances from the edge of the original fret to the center of the new fret slot. Use the same formulas, but measure X and F like so:
Incidentally, these formulas work for any edo. Just change the value of K. If adding frets to a 12-edo guitar to convert it to 24edo:
- K = 24th root of 2 = 2 ^ (1/24) = 1.0293
- 1/K = 2 ^ (-1/24)= 0.9715
Fret markers
On an even-frets layout, dots (fretboard markers) are placed every 4 frets in a cycle of single-double-triple. So, the 4th fret has a single dot, the 8th fret has double dots, the 12th fret has triple dots, and then the 16th fret is back to single, and so on. Thus, a 36-fret guitar (pictured) has 18 dots on 9 frets, and a 41-fret guitar has 19 dots on 10 frets.
The small dots on the side of the neck follow the same single/double/triple pattern. The double and triple dots are oriented like the usual 12-equal double dots. At the 36th fret, the triple dots are too wide to fit between the frets. This is not a problem if there is no binding and each fret's tang stops short of the edge of the fretboard, as is the case with the removable b-fret shown above. Otherwise, only the 35th and 36th frets can have their tangs stop short. As a last resort, the triple side dots can be placed in a triangle.
Because the frets get closer as one goes up the neck, the double dots are closer to the triple dots than the single dots. As a result, if the distance between the double dots is the same as the distance between any two of the triple dots, the side of each "kite" formed by the dots is a concave line. To make a nice straight line, use the spreadsheet from above.
DIY frets
By far the largest expense of a conversion is the fretwork. For a cheap conversion, one can defret a guitar, fill the old fret slots with wood filler, and then create new frets without using fretwire.
To remove the frets, use a pair of end nippers. Grind away the front a bit so that the cutting edge is at the absolute front of the pliers. First use a soldering iron or an ordinary laundry iron to heat the fret, to weaken the glue. Touch the fret as you do this, to monitor the temperature. Too much heat will burn the fretboard. Then pull up the fret with the nippers, getting the cutting edges underneath the top of the fret. Start at one end of the fret and work your way to the other end.
There are several materials that can substitute for fretwire, all metal except for the last:
- each shaft of a cotter pin
- half-round dental clasp wire
- tangless fretwire meant for Parker guitars
- tangless fretwire from Sintoms.com
- fretlets from John Schneider
- short sections of an old guitar string (good for a radiused fretboard)
- plastic cable ties aka zip ties (easiest to install)
For the guitar string sections, use packaging tape over the fret. For the other metal materials, use double-sided sticky tape under the fret. Check the placement with an electronic tuner.
Cable ties
Cable ties work better with a nylon-string guitar than a steel-string. Use cable ties that are as narrow as possible. If needed, trim the tie with scissors, as shown in the photo. To get the cable tie to lie as flat as possible on the fretboard, pre-crimp the cable tie with pliers, as pictured.
Various cable-tie sources:
- www.gardnerbender.com/en/p/46-206UVB/Cable-Tie-6-inch-30-lb-Black# (narrow but short)
- www.doitbest.com/product/500740/do-it-7-in-x-0-189-in-black-molded-nylon-weather-resistant-cable-tie-20-pack-500740/
- byjasco.com/power-gear-plastic-cable-ties-8in-100pk-clear-0 (long and narrow, but can't take much tension)
The little box that you feed the end of the cable tie through tends to get in the way of playing. If you never fret with your thumb, you might want to position the boxes along the bass edge of the fretboard. Or you can position them in the middle of the neck (pictured below). After you install a cable tie, clip off the "tail" with a nail clipper, as close to the box as you possibly can. Install the cable tie for the highest fret first. Tighten it around the narrower part of the neck, then push it up to the wider part, using the neck's taper to get an extremely snug fit. To tighten the last few cable ties, grab the tail with needlenose pliers, as close to the box as you can, with the pliers perpendicular to the tail. Then for maximum leverage, tighten using a twisting motion, rotating the pliers along its long axis, wrapping the tail around the needlenose. Finally, you can shove the clipped-off tails from the other frets under those last few cable ties. Once they are all installed, cover the back of the neck with a few layers of painter's tape to make them more comfortable and less likely to slip out of position.
String Gauges
A 6-string Kite guitar tuned in 3rds can be strung with a standard set of strings, but it's not ideal. The high strings will be somewhat slack, and the low strings will be somewhat tight. To find the appropriate gauges, use the D'Addario method: calculate each string's tension from its unit weight, length and pitch (frequency) by the formula T = UW x (2 x L x F)2 / 386.4. For open strings, the length is the guitar's scale. The frequency in hertz of the Nth string of 8 strings tuned in the standard downmajor 3rds with a low string of vD is 440 * (2 ^ (-7/12 + (21 - 13*N) / 41)). For a 6-string guitar in mid-6 tuning, N ranges from 2 to 7. Or use the frequency table below. The unit weight is pounds per inch, and is a function of string gauge and string type (plain vs. wound, etc.). Unit weights for a given gauge vary by manufacturer. One can work backwards from this and select string gauges/types that give uniform tensions. The formula is UW = (T x 386.4) / (2 x L x F)2.
The desired tension depends on the instrument, and of course personal taste. A steel-string acoustic guitar might have 25-30 lbs. tension for each string. A 12-equal 25.5" electric guitar strung with a standard 10-46 set has 15-20 lbs per string. With a 9-42 set it has 13-16 lbs. A 34" electric bass with a standard 45-100 set has 35-50 lbs.
- A longer scale means a higher tension or a smaller gauge or a lower pitch (frequency)
- A higher tension means a longer scale or a bigger gauge or a higher pitch
- A bigger gauge means a shorter scale or a higher tension or a lower pitch
- A higher pitch means a shorter scale or a higher tension or a smaller gauge
Stringjoy has an online tension calculator.
GHS Strings has various string tension guides:
D'Addario has published their unit weights, thus the individual tensions can be calculated for a given set of strings. This spreadsheet contains their products with their unit weights: TallKite.com/misc_files/StringTensionCalculator.ods.
Microtonalist and luthier Tom WInspear can provide custom string sets at his website www.winspearinstrumental.com. His approach is to extrapolate from familiar string sets. He says this about string gauges: "Gauges can be scaled at the same ratios as frequency. A 41-equal downmajor 3rd is 2^(13/41) = 1.2458, thus from string to string the gauge changes by 24.58%. But you can't do that across the plain to wound transition. To tune to different keys, increase the gauges by 5.95% for each 12-equal semitone of transposition, or 1.705% for each 41-equal step. All this assumes a 25.5" scale. For a scale of S inches, multiply each gauge by 25.5/S and round off. For scales longer than 25.5", err on the side of heavier and round up, as longer scales do feel more flexible loaded with the same tension. Likewise, for scales less than 25.5", err on the side of lighter and round down. However, the plain strings should always be rounded slightly down, and should utilize .0005" increment plain strings where available."
JustStrings.com and StringsByMail.com both sell custom gauges singly or in bulk. Individual Savarez nylon strings in various gauges: StringsByMail.com/classical-guitar-strings-1/savarez-62/savarez-specialty-singles-147/alliance-kf-carbon-602/alliance-kf-1-meter-460
| scale | low note | gauges (p = plain, w = wound) | source | notes | |
|---|---|---|---|---|---|
| acoustic guitar | 25.5" | vD | 12 15 19p/20w 25 32 40 48 59 | StringJoy | Phosphor Bronze |
| 27" | vD | 11.5 15 18p 24w 30 36 46 56 | D'Addario | somewhat light | |
| electric guitar | 25.5-26.5" | vD | 10 13 16 19p/22w 26 34 42 52 | D'Addario | |
| 25.5" | vD | 10 11.5 15 19p/20w 26 32 40 50 | StringJoy | Nickel Wound | |
| electric bass | 34" | vD | 40 55 70 80 95 110/115 | StringJoy | Nickel Wound |
| classical guitar | 25.5" | ^^F | 24.4 26.0 30.3p 24w 28 33 40 high 3 strings in mm: 62 66 77 |
high 3: Savarez KF low 4: Silverwound |
Fretboard placement
When building a guitar, the bridge/saddle is positioned relative to the fretboard. When converting a guitar, the fretboard is positioned relative to the bridge/saddle. This process is like saddle compensation, but instead of moving the saddle points back and forth, one moves the entire fretboard back and forth.
On an electric guitar, the saddle points are adjustable, so the fretboard placement need be only roughly correct. But on an acoustic or classical guitar, it's crucial to place the fretboard accurately.
When gluing on the fretboard, unless it's an electric, be sure to use locator pins! This is a standard (non-microtonal) luthier practice, google "fretboard locator pins". With the fretboard clamped onto the neck, drill two (some suggest three or four) 1/16" guide holes through the fretboard and partway into the neck, to position the neck during glue-up. Drill the holes in the fret slots so that the frets will hide the holes. Drill on either side of the fretboard to avoid the truss rod. Drill one hole at the first fret slot and the other near the top of the neck. Do not drill into the body. Unclamp the fretboard and put 1/16" locating pins in the guide holes to position the fretboard exactly. Glue the fretboard on. Once the glue is dry, carefully remove the locator pins. Do one final levelling on the fretboard along each string path, then install the frets.
Method #1
Before removing the old fretboard, check the intonation. Assuming it's on, mark the location of the old (12edo) 7th fret on both sides of the neck. Do the same with the old 17th fret by putting tape on the guitar body on both sides of the fretboard. We'll be using these 4 guide marks to place the new (41edo) fretboard.
If the intonation is off, use a formula to convert the error in cents to an error in millimeters or inches. This formula is given in the section below on saddle compensation. We're doing saddle compensation in reverse: rather than moving the saddle points, we're moving the guide marks.
Remove the old fretboard. Use the guide marks to position the new fretboard, which at this point has no frets in it. The new 12th fret slot will be only 2.5¢ closer to the soundhole than the old 7th fret. And the new 29th fret slot will be 2.5¢ further from the soundhole than the old 17th fret. That 2.5¢ distance will be almost twice as large for the new 12th fret as for the new 29th fret (almost twice because a 34\41 minor 7th is almost an octave). So eyeball the marks and the fret slots until it looks right on both sides of the neck/body.
Method #2
Remove the old fretboard. Put the frets on the new fretboard. Then clamp it to the neck using narrow wooden blocks that won't interfere with the strings. Then string it up, test the intonation, and adjust the fretboard placement as needed (see below). Finally, mark the correct position, remove the strings, and glue down the fretboard.
But many luthiers prefer to install the frets after the fretboard is attached, so that they can do one final levelling on the fretboard along each string path. If so, only install those frets needed for intonation. After gluing down the fretboard, remove those few frets, level, and then install all the frets.
These pictures illustrate the clamping on a standard 12-equal guitar:
Always install at least two frets, because the nut might need compensation (see below), and can't be trusted yet. One might use frets 1 and 13 to get a fifth, or frets 0.5 (the a-fret) and 21 to get an octave. Or one might install 3 or 4 frets, for safety. Check the tuning at all the frets and all the strings, using Method #2 below. Then place the fretboard.
Saddle and nut compensation
Since the Kite guitar is so much more in tune than a 12-equal guitar, extra care should be taken with compensation. On an electric guitar, one can simply dial in the correct saddle compensation. On an acoustic or classical, one must file the saddle.
Short answer
For each string, match the 41st fret harmonic exactly with the fretted note, using a tuner. You can also match the 12th fret harmonic with the 12th fret note, which will be 1 octave lower. (To be precise, the fretted note should be half a cent sharper than the harmonic.) Ideally check at both the 12th and 41st frets, and split the difference to get both as in tune as possible.
Long answer
Method #1: To find the saddle compensation on a standard guitar, one compares the harmonic at the 12th fret with the fretted note at the 12th fret. For the Kite guitar, by a weird coincidence, one does the same! But the 12th fret now makes the 3rd harmonic, not the 2nd. Thus the two notes should be an octave apart, not a unison. If using a tuner, this is not a problem. But if using your ear, a unison is easier to hear than an octave. To get a unison, when you fret the string, play the 2nd harmonic with your other hand. With your forefinger or middle finger, touch the string midway between the 32nd and 33rd frets. Then stretch your hand and pluck with your thumb as close as you can get to the midpoint between your finger and the bridge. If this isn't feasible (e.g. with a bass guitar), you can capo the string at the 12th fret and use both hands to play the harmonic. (And to be extremely precise, the fretted note should be 0.48¢ sharper than the harmonic. The 3rd harmonic is 701.96¢ and the 41-equal interval is 702.44¢.)
On a standard guitar, there's a formula for saddle compensation. Move the saddle point back (i.e. away from the soundhole) by about 0.015" for every cent that the 12th fret note is sharp of the open string's 2nd harmonic. The 0.015" figure is more precisely the scale length times ln(2)/1200, which is approximately scaleLength/1731. Saddle compensation flattens the 12th fret note twice as much as the open string note. So if the 12th fret note is 3¢ sharp, flattening the open string note by 3¢ (about 0.045") flattens the 12th fret note by 6¢, and the interval between them is flattened by 3¢ to an exact octave.
The following table gives more precise values of this 0.015" figure for various scale lengths. For example, for a 27" guitar, if the note is 10¢ sharp, move the saddle point back 0.156".
| imperial | metric | ||
|---|---|---|---|
| scale length | mil per cent | scale length | mm per cent |
| 24.5" | 14.2 | 640mm | 0.370mm |
| 25" | 14.4 | 645mm | 0.373mm |
| 25.5" | 14.7 | 650mm | 0.375mm |
| 26" | 15.0 | 655mm | 0.378mm |
| 26.5" | 15.3 | 660mm | 0.381mm |
| 27" | 15.6 | 665mm | 0.384mm |
On a Kite guitar, the scaleLength/1731 formula still holds. But saddle compensation affects the 12th fret note only one and a half times as much as the open string note. (Because an octave has frequency ratio 2/1 = twice as much, and a fifth has 3/2 = one and a half as much.) Hence for each cent of sharpness, one must flatten by two cents.
For example, suppose the 12th fret note is 2¢ sharp of the 3rd harmonic. It's supposed to be 0.48¢ sharp, so the actual sharpness is only 1.5¢. (In practice, if one's tuner isn't this accurate, one might simply round down a bit.) Move the saddle point back by twice this, 3¢ or 0.045". This will flatten the open string by 3¢ and the 12th fret note by 4.5¢, narrowing the interval by 1.5¢ to an exact 41-equal 5th. On the saddle, mark a point 0.045" behind the exit point, and file up to the mark.
Alternative method #1: If the guitar has a 41st fret, compensation can be done more easily and accurately by comparing the harmonic at the 41st fret (the 4th harmonic) with the fretted note at the 41st fret. They should be an exact unison, so no need to subtract a half cent, and no need to play the harmonic of the fretted note. The 4th harmonic is a double octave, with frequency ratio 4/1, so saddle compensation affects the 41st fret note four times as much as the open string note. Hence for each cent of sharpness, one must flatten by one-third cent.
In the previous example, the 12th fret harmonic was 2¢ sharper than the fretted note. This would make the 41st fret note 9¢ sharp of the 4th harmonic. Move the saddle point back by 1/3 this, 3¢ or 0.045". This will flatten the open string by 3¢ and the 41st fret note by 12¢, narrowing the interval by 9¢ to an exact double octave. This method is more accurate because tuners aren't perfect, and an error affects the compensation distance only one-sixth as much. This method also works for 12-equal guitars on the 24th fret.
Other alternatives: The 8th harmonic is at fret 4 and the 10th one is at fret 3. The 9th harmonic is midway between them. Play the 8th, 9th and 10th harmonics to get a do-re-mi melody. Now play those same harmonics just a few inches from the bridge. Practice until you can cleanly play the 9th harmonic with one hand. Next play that harmonic while fretting at the 24th fret (major 9th = 9/4 ratio). The fretted harmonic should be 1 cent sharper. For every cent of sharpness above that, flatten at the saddle by four-fifths of a cent. For example, if the fretted harmonic is 6¢ sharp, that's 5 extra cents of sharpness. Move the saddle point back by four-fifths of this, 4¢. This will flatten the open string by 4¢ and the 24th fret note by 9¢, narrowing the interval by 5¢ to an exact 41-equal major 9th.
The 7th harmonic is between the 4th and 5th frets. Find that same harmonic about 3-4" from the bridge. Play it one-handed both open and while fretting at the 37th fret (minor 7th plus an 8ve = 7/2 ratio). The fretted harmonic should be 3 cents flatter. For every cent of sharpness above that, flatten at the saddle by two-fifths of a cent. For example, if the fretted harmonic is 2¢ sharp, that's 5 extra cents of sharpness. Move the saddle point back by two-fifths of this, 2¢. This will flatten the open string by 2¢ and the 37th fret note by 7¢, narrowing the interval by 5¢ to an exact 41-equal downminor 7th.
| fret | interval | ratio | harmonic | fretted note should be | for each cent of sharpness | location to play shared harmonic |
|---|---|---|---|---|---|---|
| 12 | 5th | 3/2 | 3rd | 0.5¢ sharp | flatten by two cents | 2/3 of string: between frets 32 and 33 |
| 24 | maj 9th | 9/4 | 9th | 1¢ sharp | flatten by four-fifths of a cent | 8/9 of string: past the fretboard up by the bridge |
| 37 | vmin 7th | 7/2 | 7th | 3¢ flat | flatten by two-fifths of a cent | 6/7 of string: past the fretboard up by the bridge |
| 41 | dbl 8ve | 4/1 | 4th | the same | flatten by one-third of a cent | 1/4 of string: at the same fret 41 |
Method #2: The first method serves as a rough check of the saddle points. But it's much safer to check multiple frets. If not using a microtonal tuning app, use the cents table below (printable pdf here), which has the pitch of every single note on the fretboard. The 2nd page of the pdf omits some redundant information to make room to pencil in discrepancies in cents. But the open strings aren't reliable, because the nut is not yet compensated (nut compensation must be done after saddle compensation). Use a capo to remove the nut issue. Capo the string at the 1st fret (or 2nd or 3rd, if the capo doesn't fit your 8-string very well). Tune the capo'ed string to the table, then compare the other frets to the table. Important: do not remove the capo during this process, as that will change the tension, and thus the pitch. It's usually sufficient to check every 4th fret, i.e. every dot. Look for the general trend. If the saddle point is too far back, the higher frets will be increasingly flat. Too far forward, and they will trend sharp. If there's an outlier that breaks the pattern, check its neighboring frets. No guitar is perfect. If some frets are sharp and some equally flat, that's the best you can get. Once you find the trend, estimate how much cents error would be expected at the 5th dot, which is almost an octave. That's roughly how many cents to compensate by. (To be super-precise, you could increase the cents by about 3%, so that 6¢ becomes 6.2¢.) Compensate as in method #1 with the scaleLength/1731 formula.
This next table shows the multiplicative factor for any fret distance. As we've seen, 20.5 (an octave) is 1 and 12 (a fifth) is about 2. Suppose you have a guitar with 32 frets, and you want to check the compensation using the first and last fret. From fret 1 to fret 32 is 31 frets. For each cent of sharpness, flatten by 0.540 cents. Thus if you're 10¢ sharp, flatten by 5.4¢. Since you're capoing at the 1st fret, the scale length is reduced by about 3.3%. Thus 25 1/2" becomes 24 5/8". This divided by 1731 is about 14.2 mil of compensation per cent. 14.2 x 5.4 = 77 mil = 0.077".
| frets | factor | frets | factor | frets | factor | frets | factor | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 2.486 | 20 | 1.035 | 30 | 0.569 | 40 | 0.349 | |||
| 10.5 | 2.346 | 20.5 | 1.000 | 30.5 | 0.554 | 40.5 | 0.341 | |||
| 11 | 2.220 | 21 | 0.967 | 31 | 0.540 | 41 | 0.333 | |||
| 11.5 | 2.104 | 21.5 | 0.936 | 31.5 | 0.526 | |||||
| 12 | 1.998 | 22 | 0.906 | 32 | 0.513 | |||||
| 12.5 | 1.901 | 22.5 | 0.877 | 32.5 | 0.500 | |||||
| 13 | 1.812 | 23 | 0.850 | 33 | 0.487 | |||||
| 13.5 | 1.729 | 23.5 | 0.824 | 33.5 | 0.475 | |||||
| 14 | 1.652 | 24 | 0.799 | 34 | 0.464 | |||||
| 14.5 | 1.580 | 24.5 | 0.775 | 34.5 | 0.452 | |||||
| 15 | 1.514 | 25 | 0.753 | 35 | 0.441 | |||||
| 15.5 | 1.452 | 25.5 | 0.731 | 35.5 | 0.431 | |||||
| 16 | 1.393 | 26 | 0.710 | 36 | 0.421 | |||||
| 16.5 | 1.339 | 26.5 | 0.690 | 36.5 | 0.411 | |||||
| 17 | 1.287 | 27 | 0.670 | 37 | 0.401 | |||||
| 17.5 | 1.239 | 27.5 | 0.652 | 37.5 | 0.392 | |||||
| 18 | 1.193 | 28 | 0.634 | 38 | 0.383 | |||||
| 18.5 | 1.150 | 28.5 | 0.617 | 38.5 | 0.374 | |||||
| 19 | 1.110 | 29 | 0.600 | 39 | 0.365 | |||||
| 19.5 | 1.071 | 29.5 | 0.584 | 39.5 | 0.357 | |||||
Nut compensation can be done similarly to a standard guitar, by comparing the open string to the fretted notes. But extra care might be taken here too. One can shorten the fingerboard by around 0.030" (more if the nut action is high) to slightly overcompensate, then de-compensate empirically by filing the front of the nut to move the exit points back. One can determine the exact amount to file by finding the sharpness in cents with a tuner, then using the scaleLength/1731 formula. The front of the nut can be filed lengthwise to move all the exit points at once, or up and down to move individual exit points.
Placing the saddle: If you're building a guitar from scratch, you can find the saddle exit points empirically by placing a small rod on the bridge, under the strings, where the saddle slot will later be cut. The rod serves as a temporary saddle. Move the rod back and forth until the string is perfectly in tune. Then measure the distance from the front of the bridge to this exit point. Repeat for each string. Once you've found your exit points, you can use this spreadsheet to place the saddle slot precisely. It even tells you how wide the saddle blank needs to be. Works for any guitar, not just Kite guitars.
Final notes:
- String gauges affect compensation, so try to choose the correct gauges first.
- One can avoid nut compensation by using a zero fret or by having a very low action.
- Adjustable saddle and nut for acoustic guitars (similar to electric guitars): https://www.portlandguitar.com/collections/bridges
For more on saddle and nut compensation, see
- https://www.doolinguitars.com/intonation/intonation4.html (Mike Doolin)
- https://www.portlandguitar.com/pages/guitar-intonation (Jay Dickinson)
- https://www.portlandguitar.com/pages/perfect-intonation-long-version (Jay Dickinson)
- http://schrammguitars.com/intonation.html (John and William Gilbert)
- https://www.proguitar.com/academy/guitar/intonation/byers-classical (Greg Byers)
String spacing
With 7 or 8 strings, it's important to avoid both a too-wide neck and a too-tight string spacing. Every millimeter counts. One can reduce neck width by minimizing the distance from the outer string to the edge of the fretboard (known as the "reveal"). To do this, minimize the amount of rounding of the edge of the fretboard. And preserve as much usable fret length as possible by beveling the ends of the frets at a steeper angle and not over-rounding the shoulder of the fret where the top and the end meet.
The spacing can be slightly improved further as follows:
Conventional wisdom holds that there are two ways to space the strings: center-to-center (C2C) and edge-to-edge (E2E). For the right hand, E2E is better than C2C, because otherwise it's harder to fit one's finger between the thicker strings. E2E spacing ensures that the gap between strings is uniform, and each string is equally easy to pluck.
On the left hand, if the spacing is too tight, when one frets a string and plays the neighboring string either open or fretted further back, the finger can dampen the neighboring string. Thus the important gap is the gap between every other string. That is, when fretting the 2nd string, the important gap is between the inner edges of the 1st and 3rd strings. When fretting the 3rd string, it's between the 2nd and 4th string. (When fretting the 1st string, the gap is between the 1st and 2nd string, but if the 2nd string is more or less in the center of the 1st-to-3rd gap, the 1st-to-2nd gap will be sufficiently large.)
This spacing is called edge-to-next-edge (E2NE). It is different from the other two spacings. C2C spacing results in the thicker strings being more crowded and harder to fret cleanly. E2E spacing results in the thinner strings being more crowded.
But specifying that these gaps be uniform doesn't completely specify E2NE spacing, because one could shift every other string sideways without changing these gaps. So we need an additional requirement. Ideally each string should be midway between the nearest edges of the two neighboring strings, i.e. perfectly centered in its gap. The center-to-edge spacing would be constant for each string. But this is impossible. For example, the distance from the center of the 2nd string to the nearest edge of the 3rd string must be less than the distance from the center of the 3rd string to the nearest edge of the 2nd string, because the 2nd string is thinner.
It is not yet known how to maximize centeredness. Consider the center of the 2nd string, and the center of the gap between the 1st and 3rd strings' edges. Let x be the distance between the two, measured so that positive x corresponds to being closer to the 1st string. Each string except the 1st and last will have a similar distance from the center of the gap it is in, measured in the same direction, called its off-centeredness. This distance is different from x but utterly dependent on it. For a given set of string gauges, how can one find the x that minimizes all the off-centerednesses? For gauges 11.5 15 18 24 30 36 46 56, the best x is zero.
In the next table, R1, R2, etc. is the radius of each string, and D is a constant roughly equal to 1/7th of the nut width. The value of D is not consistent from column to column. In E2E spacing, all off-centerednesses are zero. In C2C spacing, each string is off-center towards its thicker neighbor.
| C2C | E2E | E2NE | E2NE off-centeredness | |
|---|---|---|---|---|
| 2nd string | D | D + R1 + R2 | D - x + R1 | x |
| 3rd string | 2D | 2D + R1 + 2R2 + R3 | 2D + R1 + R3 | -x - (R3-R2) |
| 4th string | 3D | 3D + R1 + 2R2 + 2R3 + R4 | 3D - x + R1 + R2 + R4 | x + (R3-R2) - (R4-R3) |
| 5th string | 4D | 4D + R1 + 2R2 + 2R3 + 2R4 + R5 | 4D + R1 + 2R3 + R5 | -x - (R3-R2) + (R4-R3) - (R5-R4) |
| 6th string | 5D | 5D + R1 + 2R2 + 2R3 + 2R4 + 2R5 + R6 | 5D - x + R1 + R2 + 2R4 + R6 | x + (R3-R2) - (R4-R3) + (R5-R4) - (R6-R5) |
| 7th string | 6D | 6D + R1 + 2R2 + 2R3 + 2R4 + 2R5 + 2R6 + R7 | 6D + R1 + 2R3 + 2R5 + R7 | -x - (R3-R2) + (R4-R3) - (R5-R4) + (R6-R5) - (R7-R6) |
| 8th string | 7D | 7D + R1 + 2R2 + 2R3 + 2R4 + 2R5 + 2R6 + 2R7 + R8 | 7D - x + R1 + R2 + 2R4 + 2R6 + R8 | (N/A) |
Note that the nut is slotted edge-to-next-edge but the bridge is edge-to-edge, so as one plays further up the neck, the spacing deviates from the ideal. Furthermore each string's sideways movement increases as you get away from the nut. But the spacing widens further up the neck, making fretting cleanly easier, so this is not a problem.
Resources
Graphtech.com carries a wide variety of tusq saddles (synthetic ivory) as well as other guitar parts.
Thomastik-infeld.com sells kf110 string sets, which are low-tension steel strings that supposedly can be used on a classical guitar.
Microtonal tuning apps that use 41-equal: Kite_Guitar#Tuning_software_options
Tables
Notes
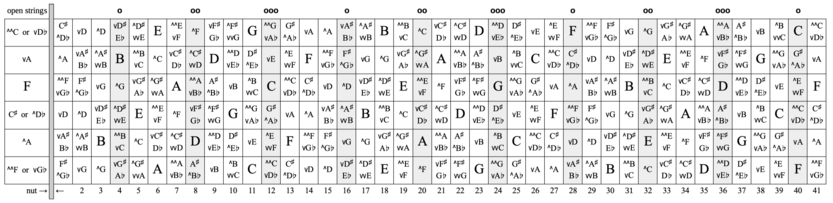
6-string (mid-6), downmajor 3rds tuning
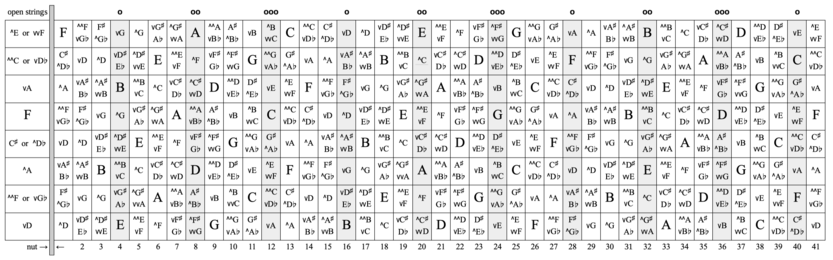
8-string (full-8), downmajor 3rds tuning
Cents
Every note on the Kite Guitar fretboard (printable pdf here). The outer columns show the dots on the fretboard. The low note is vD and the tuning is in downmajor 3rds. The note names in the table are 12-equal, not 41-equal. Thus the lowest note, which in 41-equal is named vD, is here named "D -29.3", meaning 12-equal D minus 29.3¢. The 7 natural notes in 41-equal are bolded and underlined italic. There's usually one note, called the anchor note, that agrees with the standard tuning exactly. The anchor note here is D, thus the D note on the 6th string, 8th fret is +0.0¢.
| 8th string | 7th string | 6th string | 5th string | 4th string | 3rd string | 2nd string | 1st string | |||||||||||
| 0 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | D | +29.3 | F# | +9.8 | Bb | -9.8 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | ||
| 2 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | D | +29.3 | F# | +9.8 | Bb | -9.8 | D | -29.3 | F# | -48.8 | ||
| 3 | Eb | +46.3 | G | +26.8 | B | +7.3 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | D | +29.3 | F# | +9.8 | ||
| * | 4 | E | +4.9 | G# | -14.6 | C | -34.1 | Eb | +46.3 | G | +26.8 | B | +7.3 | Eb | -12.2 | G | -31.7 | * |
| 5 | F | -36.6 | G# | +43.9 | C | +24.4 | E | +4.9 | G# | -14.6 | C | -34.1 | Eb | +46.3 | G | +26.8 | ||
| 6 | F | +22.0 | A | +2.4 | C# | -17.1 | F | -36.6 | G# | +43.9 | C | +24.4 | E | +4.9 | G# | -14.6 | ||
| 7 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | F | +22.0 | A | +2.4 | C# | -17.1 | F | -36.6 | G# | +43.9 | ||
| * * | 8 | F# | +39.0 | Bb | +19.5 | D | +0.0 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | F | +22.0 | A | +2.4 | * * |
| 9 | G | -2.4 | B | -22.0 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | D | +0.0 | F# | -19.5 | Bb | -39.0 | ||
| 10 | G# | -43.9 | B | +36.6 | Eb | +17.1 | G | -2.4 | B | -22.0 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | ||
| 11 | G# | +14.6 | C | -4.9 | E | -24.4 | G# | -43.9 | B | +36.6 | Eb | +17.1 | G | -2.4 | B | -22.0 | ||
| * * * | 12 | A | -26.8 | C# | -46.3 | E | +34.1 | G# | +14.6 | C | -4.9 | E | -24.4 | G# | -43.9 | B | +36.6 | * * * |
| 13 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | G# | +14.6 | C | -4.9 | ||
| 14 | Bb | -9.8 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | ||
| 15 | Bb | +48.8 | D | +29.3 | F# | +9.8 | Bb | -9.8 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | ||
| * | 16 | B | +7.3 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | D | +29.3 | F# | +9.8 | Bb | -9.8 | D | -29.3 | * |
| 17 | C | -34.1 | Eb | +46.3 | G | +26.8 | B | +7.3 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | D | +29.3 | ||
| 18 | C | +24.4 | E | +4.9 | G# | -14.6 | C | -34.1 | Eb | +46.3 | G | +26.8 | B | +7.3 | Eb | -12.2 | ||
| 19 | C# | -17.1 | F | -36.6 | G# | +43.9 | C | +24.4 | E | +4.9 | G# | -14.6 | C | -34.1 | Eb | +46.3 | ||
| * * | 20 | C# | +41.5 | F | +22.0 | A | +2.4 | C# | -17.1 | F | -36.6 | G# | +43.9 | C | +24.4 | E | +4.9 | * * |
| 21 | D | +0.0 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | F | +22.0 | A | +2.4 | C# | -17.1 | F | -36.6 | ||
| 22 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | D | +0.0 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | F | +22.0 | ||
| 23 | Eb | +17.1 | G | -2.4 | B | -22.0 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | D | +0.0 | F# | -19.5 | ||
| * * * | 24 | E | -24.4 | G# | -43.9 | B | +36.6 | Eb | +17.1 | G | -2.4 | B | -22.0 | Eb | -41.5 | F# | +39.0 | * * * |
| 25 | E | +34.1 | G# | +14.6 | C | -4.9 | E | -24.4 | G# | -43.9 | B | +36.6 | Eb | +17.1 | G | -2.4 | ||
| 26 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | G# | +14.6 | C | -4.9 | E | -24.4 | G# | -43.9 | ||
| 27 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | G# | +14.6 | ||
| * | 28 | F# | +9.8 | Bb | -9.8 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | * |
| 29 | G | -31.7 | Bb | +48.8 | D | +29.3 | F# | +9.8 | Bb | -9.8 | D | -29.3 | F# | -48.8 | A | +31.7 | ||
| 30 | G | +26.8 | B | +7.3 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | D | +29.3 | F# | +9.8 | Bb | -9.8 | ||
| 31 | G# | -14.6 | C | -34.1 | Eb | +46.3 | G | +26.8 | B | +7.3 | Eb | -12.2 | G | -31.7 | Bb | +48.8 | ||
| * * | 32 | G# | +43.9 | C | +24.4 | E | +4.9 | G# | -14.6 | C | -34.1 | Eb | +46.3 | G | +26.8 | B | +7.3 | * * |
| 33 | A | +2.4 | C# | -17.1 | F | -36.6 | G# | +43.9 | C | +24.4 | E | +4.9 | G# | -14.6 | C | -34.1 | ||
| 34 | Bb | -39.0 | C# | +41.5 | F | +22.0 | A | +2.4 | C# | -17.1 | F | -36.6 | G# | +43.9 | C | +24.4 | ||
| 35 | Bb | +19.5 | D | +0.0 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | F | +22.0 | A | +2.4 | C# | -17.1 | ||
| * * * | 36 | B | -22.0 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | D | +0.0 | F# | -19.5 | Bb | -39.0 | C# | +41.5 | * * * |
| 37 | B | +36.6 | Eb | +17.1 | G | -2.4 | B | -22.0 | Eb | -41.5 | F# | +39.0 | Bb | +19.5 | D | +0.0 | ||
| 38 | C | -4.9 | E | -24.4 | G# | -43.9 | B | +36.6 | Eb | +17.1 | G | -2.4 | B | -22.0 | Eb | -41.5 | ||
| 39 | C# | -46.3 | E | +34.1 | G# | +14.6 | C | -4.9 | E | -24.4 | G# | -43.9 | B | +36.6 | Eb | +17.1 | ||
| * | 40 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | G# | +14.6 | C | -4.9 | E | -24.4 | * |
| 41 | D | -29.3 | F# | -48.8 | A | +31.7 | C# | +12.2 | F | -7.3 | A | -26.8 | C# | -46.3 | E | +34.1 | ||
This table shows every note in 41-equal, not as notes on the fretboard, but as a simple list of all 41. The pitch relative to 12-equal depends on the anchor note. 5 different anchor notes are shown.
| C anchor | G anchor | D anchor | A anchor | E anchor | ||
|---|---|---|---|---|---|---|
| C | C +0¢ | C -2¢ | C -5¢ | C -7¢ | C -10¢ | C |
| ^C | C +29¢ | C +27¢ | C +24¢ | C +22¢ | C +20¢ | ^C |
| ^^C / vDb | C# -41¢ | C# -44¢ | C# -46¢ | C# -49¢ | C +49¢ | ^^C / vDb |
| vC# / Db | C# -12¢ | C# -15¢ | C# -17¢ | C# -20¢ | C# -22¢ | vC# / Db |
| C# / ^Db | C# +17¢ | C# +15¢ | C# +12¢ | C# +10¢ | C# +7¢ | C# / ^Db |
| ^C# / vvD | C# +46¢ | C# +44¢ | C# +41¢ | C# +39¢ | C# +37¢ | ^C# / vvD |
| vD | D -24¢ | D -27¢ | D -29¢ | D -32¢ | D -34¢ | vD |
| D | D +5¢ | D +2¢ | D +0¢ | D -2¢ | D -5¢ | D |
| ^D | D +34¢ | D +32¢ | D +29¢ | D +27¢ | D +24¢ | ^D |
| ^^D / vEb | Eb -37¢ | Eb -39¢ | Eb -41¢ | Eb -44¢ | Eb -46¢ | ^^D / vEb |
| vD# / Eb | Eb -7¢ | Eb -10¢ | Eb -12¢ | Eb -15¢ | Eb -17¢ | vD# / Eb |
| D# / ^Eb | Eb +22¢ | Eb +20¢ | Eb +17¢ | Eb +15¢ | Eb +12¢ | D# / ^Eb |
| ^D# / vvE | E -49¢ | Eb +49¢ | Eb +46¢ | Eb +44¢ | Eb +41¢ | ^D# / vvE |
| vE | E -20¢ | E -22¢ | E -24¢ | E -27¢ | E -29¢ | vE |
| E | E +10¢ | E +7¢ | E +5¢ | E +2¢ | E +0¢ | E |
| ^E | E +39¢ | E +37¢ | E +34¢ | E +32¢ | E +29¢ | ^E |
| vF | F -32¢ | F -34¢ | F -37¢ | F -39¢ | F -41¢ | vF |
| F | F -2¢ | F -5¢ | F -7¢ | F -10¢ | F -12¢ | F |
| ^F | F +27¢ | F +24¢ | F +22¢ | F +20¢ | F +17¢ | ^F |
| ^^F / vGb | F# -44¢ | F# -46¢ | F# -49¢ | F +49¢ | F +46¢ | ^^F / vGb |
| vF# / Gb | F# -15¢ | F# -17¢ | F# -20¢ | F# -22¢ | F# -24¢ | vF# / Gb |
| #F / ^Gb | F# +15¢ | F# +12¢ | F# +10¢ | F# +7¢ | F# +5¢ | #F / ^Gb |
| ^F# / vvG | F# +44¢ | F# +41¢ | F# +39¢ | F# +37¢ | F# +34¢ | ^F# / vvG |
| vG | G -27¢ | G -29¢ | G -32¢ | G -34¢ | G -37¢ | vG |
| G | G +2¢ | G +0¢ | G -2¢ | G -5¢ | G -7¢ | G |
| ^G | G +32¢ | G +29¢ | G +27¢ | G +24¢ | G +22¢ | ^G |
| ^^G / vAb | G# -39¢ | G# -41¢ | G# -44¢ | G# -46¢ | G# -49¢ | ^^G / vAb |
| vG# / Ab | G# -10¢ | G# -12¢ | G# -15¢ | G# -17¢ | G# -20¢ | vG# / Ab |
| G# / ^Ab | G# +20¢ | G# +17¢ | G# +15¢ | G# +12¢ | G# +10¢ | G# / ^Ab |
| ^G# / vvA | G# +49¢ | G# +46¢ | G# +44¢ | G# +41¢ | G# +39¢ | ^G# / vvA |
| vA | A -22¢ | A -24¢ | A -27¢ | A -29¢ | A -32¢ | vA |
| A | A +7¢ | A +5¢ | A +2¢ | A +0¢ | A -2¢ | A |
| ^A | A +37¢ | A +34¢ | A +32¢ | A +29¢ | A +27¢ | ^A |
| ^^A / vBb | Bb -34¢ | Bb -37¢ | Bb -39¢ | Bb -41¢ | Bb -44¢ | ^^A / vBb |
| vA# / Bb | Bb -5¢ | Bb -7¢ | Bb -10¢ | Bb -12¢ | Bb -15¢ | vA# / Bb |
| A# / ^Bb | Bb +24¢ | Bb +22¢ | Bb +20¢ | Bb +17¢ | Bb +15¢ | A# / ^Bb |
| ^A# / vvB | B -46¢ | B -49¢ | Bb +49¢ | Bb +46¢ | Bb +44¢ | ^A# / vvB |
| vB | B -17¢ | B -20¢ | B -22¢ | B -24¢ | B -27¢ | vB |
| B | B +12¢ | B +10¢ | B +7¢ | B +5¢ | B +2¢ | B |
| ^B | B +41¢ | B +39¢ | B +37¢ | B +34¢ | B +32¢ | ^B |
| vC | C -29¢ | C -32¢ | C -34¢ | C -37¢ | C -39¢ | vC |
| C | C +0¢ | C -2¢ | C -5¢ | C -7¢ | C -10¢ | C |
| C anchor | G anchor | D anchor | A anchor | E anchor |
Frequencies
41-equal frequencies in Hertz. The anchor note D is tuned to standard A-440 pitch. vA is roughly 432hz, and vvB is roughly the ubiquitous 60hz electrical hum.
| 0th octave | 1st octave | 2nd octave | 3rd octave | middle-C | 5th octave | 6th octave | 7th octave | 8th octave | |
|---|---|---|---|---|---|---|---|---|---|
| C | 16.305589 | 32.611178 | 65.222357 | 130.44471 | 260.88943 | 521.77886 | 1043.5577 | 2087.1154 | 4174.2308 |
| ^C | 16.583595 | 33.167191 | 66.334382 | 132.66876 | 265.33753 | 530.67505 | 1061.3501 | 2122.7002 | 4245.4004 |
| ^^C / vDb | 16.866341 | 33.732683 | 67.465366 | 134.93073 | 269.86146 | 539.72293 | 1079.4459 | 2158.8917 | 4317.7834 |
| vC# / Db | 17.153908 | 34.307817 | 68.615633 | 137.23127 | 274.46253 | 548.92506 | 1097.8501 | 2195.7003 | 4391.4005 |
| C# / ^Db | 17.446378 | 34.892756 | 69.785512 | 139.57102 | 279.14205 | 558.28410 | 1116.5682 | 2233.1364 | 4466.2728 |
| ^C# / vvD | 17.743834 | 35.487669 | 70.975337 | 141.95067 | 283.90135 | 567.80270 | 1135.6054 | 2271.2108 | 4542.4216 |
| vD | 18.046362 | 36.092724 | 72.185449 | 144.37090 | 288.74179 | 577.48359 | 1154.9672 | 2309.9344 | 4619.8687 |
| D | 18.354048 | 36.708096 | 73.416192 | 146.83238 | 293.66477 | 587.32954 | 1174.6591 | 2349.3181 | 4698.6363 |
| ^D | 18.666980 | 37.333960 | 74.667919 | 149.33584 | 298.67168 | 597.34335 | 1194.6867 | 2389.3734 | 4778.7468 |
| ^^D / vEb | 18.985247 | 37.970494 | 75.940988 | 151.88198 | 303.76395 | 607.52791 | 1215.0558 | 2430.1116 | 4860.2232 |
| vD# / Eb | 19.308941 | 38.617881 | 77.235763 | 154.47153 | 308.94305 | 617.88610 | 1235.7722 | 2471.5444 | 4943.0888 |
| D# / ^Eb | 19.638153 | 39.276306 | 78.552613 | 157.10523 | 314.21045 | 628.42090 | 1256.8418 | 2513.6836 | 5027.3672 |
| ^D# / vvE | 19.972979 | 39.945957 | 79.891915 | 159.78383 | 319.56766 | 639.13532 | 1278.2706 | 2556.5413 | 5113.0825 |
| vE | 20.313513 | 40.627026 | 81.254051 | 162.50810 | 325.01621 | 650.03241 | 1300.0648 | 2600.1296 | 5200.2593 |
| E | 20.659853 | 41.319706 | 82.639412 | 165.27882 | 330.55765 | 661.11530 | 1322.2306 | 2644.4612 | 5288.9224 |
| ^E | 21.012098 | 42.024197 | 84.048393 | 168.09679 | 336.19357 | 672.38714 | 1344.7743 | 2689.5486 | 5379.0972 |
| vF | 21.370349 | 42.740698 | 85.481397 | 170.96279 | 341.92559 | 683.85117 | 1367.7023 | 2735.4047 | 5470.8094 |
| F | 21.734708 | 43.469416 | 86.938833 | 173.87767 | 347.75533 | 695.51066 | 1391.0213 | 2782.0426 | 5564.0853 |
| ^F | 22.105279 | 44.210559 | 88.421118 | 176.84224 | 353.68447 | 707.36894 | 1414.7379 | 2829.4758 | 5658.9515 |
| ^^F / vGb | 22.482169 | 44.964337 | 89.928675 | 179.85735 | 359.71470 | 719.42940 | 1438.8588 | 2877.7176 | 5755.4352 |
| vF# / Gb | 22.865484 | 45.730968 | 91.461936 | 182.92387 | 365.84774 | 731.69549 | 1463.3910 | 2926.7819 | 5853.5639 |
| #F / ^Gb | 23.255335 | 46.510669 | 93.021339 | 186.04268 | 372.08535 | 744.17071 | 1488.3414 | 2976.6828 | 5953.3657 |
| ^F# / vvG | 23.651832 | 47.303664 | 94.607329 | 189.21466 | 378.42931 | 756.85863 | 1513.7173 | 3027.4345 | 6054.8690 |
| vG | 24.055090 | 48.110180 | 96.220359 | 192.44072 | 384.88144 | 769.76287 | 1539.5257 | 3079.0515 | 6158.1030 |
| G | 24.465223 | 48.930446 | 97.860892 | 195.72178 | 391.44357 | 782.88714 | 1565.7743 | 3131.5485 | 6263.0971 |
| ^G | 24.882349 | 49.764698 | 99.529395 | 199.05879 | 398.11758 | 796.23516 | 1592.4703 | 3184.9406 | 6369.8813 |
| ^^G / vAb | 25.306586 | 50.613173 | 101.226346 | 202.45269 | 404.90538 | 809.81077 | 1619.6215 | 3239.2431 | 6478.4861 |
| vG# / Ab | 25.738057 | 51.476115 | 102.952229 | 205.90446 | 411.80892 | 823.61783 | 1647.2357 | 3294.4713 | 6588.9427 |
| G# / ^Ab | 26.176885 | 52.353769 | 104.707538 | 209.41508 | 418.83015 | 837.66031 | 1675.3206 | 3350.6412 | 6701.2825 |
| ^G# / vvA | 26.623194 | 53.246388 | 106.492775 | 212.98555 | 425.97110 | 851.94220 | 1703.8844 | 3407.7688 | 6815.5376 |
| vA | 27.077112 | 54.154225 | 108.308450 | 216.61690 | 433.23380 | 866.46760 | 1732.9352 | 3465.8704 | 6931.7408 |
| A | 27.538770 | 55.077541 | 110.155081 | 220.31016 | 440.62032 | 881.24065 | 1762.4813 | 3524.9626 | 7049.9252 |
| ^A | 28.008299 | 56.016599 | 112.033197 | 224.06639 | 448.13279 | 896.26558 | 1792.5312 | 3585.0623 | 7170.1246 |
| ^^A / vBb | 28.485834 | 56.971667 | 113.943335 | 227.88667 | 455.77334 | 911.54668 | 1823.0934 | 3646.1867 | 7292.3734 |
| vA# / Bb | 28.971510 | 57.943020 | 115.886039 | 231.77208 | 463.54416 | 927.08831 | 1854.1766 | 3708.3533 | 7416.7065 |
| A# / ^Bb | 29.465467 | 58.930933 | 117.861867 | 235.72373 | 471.44747 | 942.89493 | 1885.7899 | 3771.5797 | 7543.1595 |
| ^A# / vvB | 29.967845 | 59.935691 | 119.871381 | 239.74276 | 479.48553 | 958.97105 | 1917.9421 | 3835.8842 | 7671.7684 |
| vB | 30.478789 | 60.957579 | 121.915158 | 243.83032 | 487.66063 | 975.32126 | 1950.6425 | 3901.2850 | 7802.5701 |
| B | 30.998445 | 61.996890 | 123.993780 | 247.98756 | 495.97512 | 991.95024 | 1983.9005 | 3967.8010 | 7935.6019 |
| ^B | 31.526961 | 63.053921 | 126.107842 | 252.21568 | 504.43137 | 1008.86274 | 2017.7255 | 4035.4510 | 8070.9019 |
| vC | 32.064487 | 64.128974 | 128.257949 | 256.51590 | 513.03179 | 1026.06359 | 2052.1272 | 4104.2544 | 8208.5087 |
| C | 32.611178 | 65.222357 | 130.444714 | 260.88943 | 521.77886 | 1043.55771 | 2087.1154 | 4174.2308 | 8348.4617 |