Inverse-complexity-prescaled complexity

This article is a cautionary tale for anyone who (as I, Douglas Blumeyer, did) got temporarily seduced and totally confused about: using the inverse of a complexity prescaler with a complexity function, i.e. one that is in (prescaled) norm form. Inverse-complexity-prescaled complexity functions: don't use them! Now that I have good enough terminology for the constituent parts, the name itself seems as self-contradictory as the concept.

So why would someone ever want to try this? Well, I had looked into it because I was curious about the limitation of all-interval tuning schemes whereby they only work with simplicity-weight damage. I'd wondered if there was nonetheless a way to achieve complexity-weight-like effects anyway. As you will see from this article, the answer is a very slight "sort of", but at such a cost of reasonableness that there's no way it could be worth it.

For our control case, here's what normal reasonable complexity-weighting looks like, i.e. where our weight matrix [math]W[/math] increases weight with complexity, and so we call it [math]C[/math]. Again, we're using a prescaled [math]q[/math]-norm as the complexity, where [math]X[/math] is the prescaler. We've gone ahead and somewhat arbitrarily picked a demo list of target-intervals [math][\frac21, \frac32, \frac54, \frac53][/math], but at this time we want to demonstrate the general relationships here and so haven't specified the actual complexity or its prescaler yet:

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} C \\ \left[ \begin{array} {c} ‖X[1 \; 0 \; 0 \; ⟩‖_q & 0 & 0 & 0 \\ 0 & ‖X[{-1} \; 1 \; 0 \; ⟩‖_q & 0 & 0 \\ 0 & 0 & ‖X[{-2} \; 0 \; 1 \; ⟩‖_q & 0 \\ 0 & 0 & 0 & ‖X[0 \; {-1} \; 1 \; ⟩‖_q \\ \end{array} \right] \end{array} [/math]

And here's simplicity-weighting (the inverse slope of complexity-weighting, where weight is meant to decrease with complexity, and so [math]W = S[/math] instead; these changes indicated in blue) but while using the inverse of a complexity prescaler ([math]X^{-1}[/math]); these changes indicated in red):

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} {\color{blue}S} \\ \left[ \begin{array} {c} {\color{blue}\dfrac{1}{{\color{black}‖}{\color{red}X^{-1}}{\color{black}[1 \; 0 \; 0 \; ⟩‖_q}}} & 0 & 0 & 0 \\ 0 & {\color{blue}\dfrac{1}{{\color{black}‖}{\color{red}X^{-1}}{\color{black}[{-1} \; 1 \; 0 \; ⟩‖_q}}} & 0 & 0 \\ 0 & 0 & {\color{blue}\dfrac{1}{{\color{black}‖}{\color{red}X^{-1}}{\color{black}[{-2} \; 0 \; 1 \; ⟩‖_q}}} & 0 \\ 0 & 0 & 0 & {\color{blue}\dfrac{1}{{\color{black}‖}{\color{red}X^{-1}}{\color{black}[0 \; {-1} \; 1 \; ⟩‖_q}}} \\ \end{array} \right] \end{array} [/math]

Our knee-jerk guess might be that the second situation is equivalent to the first. But no, that is not true. These two inversions, the red and the blue, do not exactly cancel each other out. And only one of these two inversions is ever reasonable, with the other one introducing a ton of chaotic noise. Can you already guess which one is which?

Let's see what we'd get if we chose our default complexity, log-product [math]\text{lp-C}()[/math] in this case. This means substitute in:

• [math]1[/math] in place of our norm power [math]q[/math],
• the log-prime matrix [math]L[/math] in place of [math]X[/math], and
• its inverse [math]L^{-1}[/math] in place of [math]X^{-1}[/math].

Working that out, we find for our complexity-weight case:

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} C \\ \left[ \begin{array} {c} 1 & 0 & 0 & 0 \\ 0 & 2.585 & 0 & 0 \\ 0 & 0 & 4.322 & 0 \\ 0 & 0 & 0 & 3.907 \\ \end{array} \right] \end{array} [/math]

and for our "simplicity-weight" case:

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} S \\ \left[ \begin{array} {c} 1 & 0 & 0 & 0 \\ 0 & 1.631 & 0 & 0 \\ 0 & 0 & 2.431 & 0 \\ 0 & 0 & 0 & 1.062 \\ \end{array} \right] \end{array} [/math]

So we've scare-quoted "simplicity-weight" here because clearly the weights are still generally going up as complexity of the intervals goes up. And the definition of a simplicity-weight matrix we gave earlier said that the opposite should happen, i.e. that the weights should go down as complexity goes up. But also remember that we were doing a sort of weird experiment here, namely: attempting to recreate complexity-weight through a double-inversion. And so to some extent we have succeeded here. This is why earlier on we characterized these two inversions as not exactly canceling each other out. In essence, their effects do counteract each other somewhat, such that the end result is not completely unlike complexity-weight.

But that's not the whole story. We also have to account for the "chaotic noise" aspect we warned about. Now, you might have noticed that in both cases, the fourth weight is less than the third weight. This is perhaps acceptable, because it's not obvious which of [math]\frac54[/math] and [math]\frac53[/math] should be considered more complex; the former has bigger numbers but the latter has a higher "internal prime-limit" if you will. But the point is: notice that in the first case — our ordinary reasonable complexity-weighting case — the fourth weight is at least still greater than the second weight, which we should expect because surely [math]\frac53[/math] is more complex than [math]\frac32[/math] by any reasonable complexity function. But the same cannot be said about our "simplicity-weight" case, where the fourth weight is less than the second weight, or in other words, if this weighting approach claims to be giving more weight to the more complex intervals, then it also claims that [math]\frac32[/math] is more complex than [math]\frac53[/math]. And so, this is simply not a reasonable complexity function, according to the standard we just set!

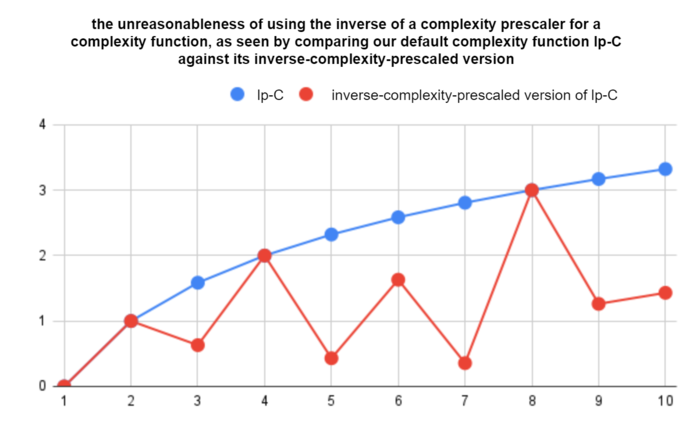
We can see this effect even more starkly if we just plot the first complexity function — again, that's our trusty default log-product complexity — against this bizarro version of it where its prescaler is inverted:

Essentially what's happened is: we still have the setup of a complexity function, where additional prime factors add more weight, however, we've flipped the relative weights of those primes so that the simpler ones count for more! In the extreme, this means that I can take some interval and add tons of factors of 131 to it (that's just an arbitrary big prime I picked) and they will hardly affect its complexity at all. This is what I meant by chaotic noise: as you move along the number line, numbers with greater numbers of smaller prime factors will be more complex than their neighbors, and so, rather than using weight proportions to smoothing out texture of prime compositions of integers along the number line, we do literally the opposite and aggravate that texture into an unpleasantly jagged craziness that no one should want to use.

Flora Canou's temperament utilities technically supports inverse-complexity-prescaled complexities, because one can set her wamount parameter to a negative value (wamount does have other legitimate reasons to be there, e.g. as Mike Battaglia's [math]s[/math] value for BOP tuning). A similar thing is also possible in my own RTT library in Wolfram Language by setting intervalComplexityNormPreTransformerPrimePower or intervalComplexityNormPreTransformerLogPrimePower to a negative value. But there's not a good reason to do it.

To clinch this point and bring it home, let's consider the two cases where we do only one of the inversions at a time. First, just the reciprocating of the weights, so we have simplicity-weighting:

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} {\color{blue}S} \\ \left[ \begin{array} {c} {\color{blue}\dfrac{1}{{\color{black}‖X[1 \; 0 \; 0 \; ⟩‖_q}}} & 0 & 0 & 0 \\ 0 & {\color{blue}\dfrac{1}{{\color{black}‖X[{-1} \; 1 \; 0 \; ⟩‖_q}}} & 0 & 0 \\ 0 & 0 & {\color{blue}\dfrac{1}{{\color{black}‖X[{-2} \; 0 \; 1 \; ⟩‖_q}}} & 0 \\ 0 & 0 & 0 & {\color{blue}\dfrac{1}{{\color{black}‖X[0 \; {-1} \; 1 \; ⟩‖_q}}} \\ \end{array} \right] \end{array} [/math]

In this case we've still got our reasonable complexity function going, and we're reciprocating it for each interval so that it does the opposite of what it would normally do. That's fine though if that's what you want. The important thing here is that the complexity values are internally consistent with each other (those are 1, 1/2.585 = 0.387, 1/4.322 = 0.231, 1/3.907 = 0.256, by the way). It's the same exact proportions of complexity from one interval to the next, but with the slope inverted.

And now here's the inversion which is always nonsensical, this time completely isolated:

[math] \begin{array} {c} \mathrm{T} \\ \left[ \begin{array} {r|r|r|r} 1 & -1 & -2 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ \end{array} \right] \end{array} \begin{array} {c} C \\ \left[ \begin{array} {c} ‖{\color{red}X^{-1}}[1 \; 0 \; 0 \; ⟩‖_q & 0 & 0 & 0 \\ 0 & ‖{\color{red}X^{-1}}[{-1} \; 1 \; 0 \; ⟩‖_q & 0 & 0 \\ 0 & 0 & ‖{\color{red}X^{-1}}[{-2} \; 0 \; 1 \; ⟩‖_q & 0 \\ 0 & 0 & 0 & ‖{\color{red}X^{-1}}[0 \; {-1} \; 1 \; ⟩‖_q \\ \end{array} \right] \end{array} [/math]

So those values are 1, 1/1.631 = 0.613, 1/2.431 = 0.411, and 1/1.062 = 0.942 by the way. So this is now our scare-quoted "complexity-weight" matrix, because our weights are generally going down as complexity goes up, but also there's the chaotic noise effect where — given that — [math]\frac53[/math] is found on the wrong side of [math]\frac32[/math].

So in conclusion, this should really be a red flag; it should never make sense to use the inverse of a complexity prescaler inside a complexity function. I do recognize that it can be confusing to realize that we do, however, use complexity functions in simplicity-weight matrices, as we did just a moment ago. Now, there is an alternative way to think of it as calling [math]\text{lp-S}()[/math] there, but I expect for most readers it is still more comfortable to think of this is as [math]\frac{1}{\text{lp-S}()}[/math]. So we do use complexity prescalers outside of the context of all-interval tunings; they may occur in any complexity-weight or simplicity-weight damage that defines its complexity as a prescaled norm of an interval vector, but we never use inverses of complexity prescalers except in the retuning magnitude, the dual norm to the interval complexity norm, for all-interval tuning schemes.