Blackwood temperament modal harmony (in 15edo)
Introduction
Blackwood[10] in 15edo refers to the 10-note symmetric 5L5s MOS scale in 15edo, which has two modes: 2 1 2 1 2 1 2 1 2 1 and 1 2 1 2 1 2 1 2 1 2. It can be thought of as a 5-limit temperament tempering out 256/243 (the Pythagorean diatonic semitone), a 7-limit temperament tempering out 28/27 and 49/48, and an 11-limit temperament tempering out 28/27, 49/48, and 55/54 (though in 15edo 121/120 and 100/99 are both tempered out as well, making the tuning identical to Ferrier and the unnamed 5c&15 temperament). In 15edo it has a period of 240 cents (5 periods per octave) and a generator of 80 or 160 cents (though it is more commonly described as having a generator of 400 cents).
Most of this page focuses on 15-EDO, perhaps the canonical Blackwood tuning (and near to the POTE tuning), but much of it is also useful for Blackwood temperament in general, even if played in other Blackwood-supported equal temperaments.
Important features of Blackwood[10] in 15edo
- 11-limit blackwood ("blacksmith") is extremely simple and efficient, and while it does fairly high damage to many ratios of 3 and 9, it does a very acceptable job of approximating most ratios of 5, 7, and 11. 9/8, 7/6, 11/9, 4/3, and their octave inversions are the most heavily-damaged, but 6/5, 12/11, and their octave inversions are tuned with good to tolerable accuracy.
- Blackwood[10] has the most 5-odd-limit consonant triads it is possible to have in a 10-note 5-limit scale.
- Because it is a 10-note scale with a period of 1/5 of an octave, any arbitrary harmony will occur either 5 or 10 times within the 10-note scale, and for otonal harmonies consisting of three or more notes, the utonal counterpart of the harmony will also occur either 5 or 10 times within the scale; this is a property that is only held by other scales with 5 periods per octave.
- Blackwood[10] is also a "mode of limited transposition" like the Diminished and Augmented scales in 12edo: since the scale is built by applying the generator only a single time within each period, the scale has only two modes.
- Another way to think about Blackwood[10] is as a superposition of seven 7-note 5-limit Fokker blocks, representing untempered variations of the diatonic modes, built on a single tonic (more on this below).
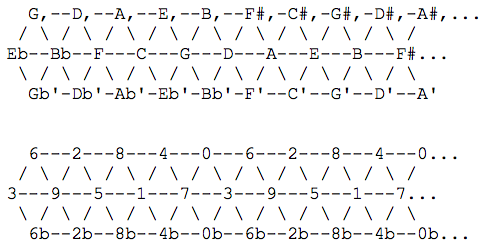
Interval Classes in Blackwood[10]
| Step of 15edo | Cent Value | Interval Class | Guitar Notation | Decimal Notation | Approximated Ratios | Pseudo-Diatonic Category |
| 0 | 0 | Unison | E | 1 | 1/1 | Unison |
| 1 | 80 | Minor 2nd, Augmented Unison* | E#, Gbb | 2b, 1# | 16/15, 21/20, 22/21, 25/24 | Minor 2nd |
| 2 | 160 | Major 2nd, Diminished 3rd | Gb, Ex | 2, 3b | 10/9, 11/10, 12/11, 15/14 | Flat Major 2nd |
| 3 | 240 | Perfect 3rd, Augmented 2nd, Diminished 4th | G | 3, 2#, 4bb | 7/6, 8/7, 9/8 | Major 2nd/Subminor 3rd |
| 4 | 320 | Minor 4th, Augmented 3rd | G#, Abb | 4b, 3# | 6/5, 11/9 | Minor 3rd |
| 5 | 400 | Major 4th, Diminished 5th | Ab, Gx | 4, 5b | 5/4, 14/11, | Major 3rd |
| 6 | 480 | Perfect 5th, Augmented 4th, Diminished 6th | A | 5, 4#, 6bb | 4/3, 21/16, 9/7 | Perfect Fourth |
| 7 | 560 | Minor 6th, Augmented 5th | A#, Bbb | 6b, 5# | 7/5, 11/8, | Augmented Fourth |
| 8 | 640 | Major 6th, Diminished 7th | Bb, Ax | 6, 7b | 10/7, 16/11 | Diminished 5th |
| 9 | 720 | Perfect 7th, Augmented 6th, Diminished 8th | B | 7, 6#, 8bb | 3/2, 32/21, 14/9 | Perfect Fifth |
| 10 | 800 | Minor 8th, Augmented 7th | B#, Dbb | 8b, 7# | 8/5, 11/7, | Minor 6th |
| 11 | 880 | Major 8th, Diminished 9th | Db, Bx | 8, 9b | 5/3, 18/11 | Major 6th |
| 12 | 960 | Perfect 9th, Augmented 8th, Diminished 10th | D | 9, 8#, 0bb | 12/7, 7/4, 16/9 | Minor 7th/Supermajor 6th |
| 13 | 1040 | Minor 10th, Augmented 9th | D#, Ebb | 0b, 9# | 9/5, 20/11, 11/6, 28/15 | Sharp Minor 7th |
| 14 | 1120 | Major 10th, Diminished Undecave | Eb, Dx | 0, 1b | 15/8, 40/21, 48/25 | Major 7th |
| 15 | 1200 | Undecave ("Octave") | E | 1 | 2/1 | Octave |
- Augmented and diminished intervals do not occur in the 10-note MOS scale, but can occur in chromatically-altered MODMOSs.
Chords of Blackwood[10]
Basic Functional Chords
All of the familiar triads and tetrads of the diatonic scale are found plentifully in Blackwood[10], which is pretty obvious when you just look at the notes available in the major and minor modes:
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11-ave | |
| Major Mode (cents) | 0 | 160 | 240 | 400 | 480 | 640 | 720 | 880 | 960 | 1120 | 1200 |
| Minor Mode (cents) | 0 | 80 | 240 | 320 | 480 | 560 | 720 | 800 | 960 | 1040 | 1200 |
Looking at this table, one can see approximations to all sorts of functional chords; if it's not immediately obvious, I'll spell it out in the following tables:
| Diatonic Chord Name | Decatonic Name
(if different) |
Tuning (cents) | Spelling 1 | Spelling 2 | Degrees of Major Mode Found On: | Degrees of Minor Mode Found On: |
| Major Triad | Same | 0-400-720 | E-Ab-B | 1-4-7 | Odd | Even |
| Minor Triad | Same | 0-320-720 | E-G#-B | 1-4b-7 | Even | Odd |
| Diminished | Same | 0-320-560 | E-G#-A# | 1-4b-6b | Even | Odd |
| Sus2 | Sus3 | 0-240-720 | E-G-B | 1-3-7 | All | All |
| Sus4 | Sus5 | 0-480-720 | E-A-B | 1-5-7 | All | All |
| Major 7th (maj7) | Major 10th | 0-400-720-1120 | E-Ab-B-Eb | 1-4-7-0 | Odd | Even |
| Minor 7th (min7) | Minor 10th | 0-320-720-1040 | E-G#-B-D# | 1-4b-7-0b | Even | Odd |
| Dominant 7th (7) | Major 9th | 0-400-720-960 | E-Ab-B-D | 1-4-7-9 | Odd | Even |
| Half-Diminished 7th (m7b5) | Diminished 10th | 0-320-560-1040 | E-G#-A#-D# | 1-4b-6b-0b | Even | Odd |
| Diminished 7th | Diminished 9th | 0-320-560-960 | E-G#-A#-D | 1-4b-6b-9 | Even | Odd |
Additional Functional Chords
| Diatonic Chord Name | Decatonic Name
(if different) |
Tuning (cents) | Spelling 1 | Spelling 2 | Degrees of Major: | Degrees of Minor Mode: |
| Major 6th (M6) | Major 8th | 0-400-720-880 | E-Ab-B-Db | 1-4-7-8 | Odd | Even |
| Minor-Major 6th (m6) | Minor 9th | 0-320-720-960 | E-G#-B-D | 1-4b-7-9 | Even | Odd |
| Diminished(bb3) (Dim(bb3)) | Sus3-Maj6 | 0-240-640 | E-G-Bb | 1-3-6 | Odd | Even |
| Double-Diminished (Dim(bb3)(bb5)) | Sus3-Min6 | 0-240-560 | E-G-A# | 1-3-6b | Even | Odd |
| Major-Diminished (Maj(b5)) | Major-Sus6 | 0-400-640 | E-Ab-Bb | 1-4-6 | Odd | Even |
Chords of Extended JI & Essentially-Tempered Chords
The dominant 7th and minor-major 6th are both 7-limit chords (4:5:6:7 and 1/(4:5:6:7), respectively). The diminished triad also approximates 5:6:7. Because of the extreme tempering, it's also the case that 9:11:14 = 10:12:15 (i.e., the minor triad). There are no full otonal 11-limit hexads in the 10-note scale, but there are lots of smaller 11-limit chords (otonal, utonal, and essentially-tempered) approximated:
| Otonal Harmonics | Utonal Harmonics | Essentially-Tempered | Tuning (cents) | Spelling 1 | Spelling 2 | Degrees of Major: | Degrees of Minor: |
| 5:7:9 | 1/(6:8:11) | 0-560-1040 | |||||
| 6:7:11 | 1/(5:8:9) | 0-240-1040 | |||||
| 6:7:9:11 | 1/1-8/7-3/2-11/6 | 0-240-720-1040 | |||||
| 6:8:11 | 1/(5:7:9) | 0-480-1040 | |||||
| 7:8:9, 6:7:8 | 1/(7:8:9), 1/(6:7:8) | 0-240-480 | |||||
| 7:10:12 | 1/(9:11:16) | 1/1-16/11-7/4 | 0-640-960 | ||||
| 8:9:11 | 1/(5:6:7) | 1/1-8/7-11/8 | 0-240-560 | ||||
| 8:9:11:14 | 0-240-560-960 | ||||||
| 8:11:14 | 0-560-960 | ||||||
| 9:10:12:14 | 0-160-480-720 | ||||||
| 9:11:16 | 0-320-960 | ||||||
| 11:14:16 | 0-400-640 | ||||||
| 11:14:16:18 | 0-400-640-880 |
Diatonic Modal Harmony in Blackwood[10]
Because 15edo is not a meantone temperament, and thus does not temper out the syntonic comma of 81/80, the usual 5L2s diatonic scale is not available. In fact, in 15edo the syntonic comma, which is normally only 21.51 cents, is tuned quite wide: it is mapped to one step of 15edo, and is thus 80 cents! However, one can approximate the diatonic scale (or rather, approximate the various untempered 5-limit JI versions of it) using 3 step-sizes—a large whole tone of 240 cents representing 9/8, a small whole tone of 160 cents representing 10/9, and a semitone of 80 cents representing 16/15. Since these non-MOS diatonic scales do not temper out the syntonic comma, they will only have at most five consonant 5-limit triads (unless an 8th note is included in the right place). They may have even fewer, depending on how the steps are permuted (for instance, if the step-pattern 240-240-80-240-160-160-80 is used, only two consonant 5-limit triads are available).
However, if one insists on using only the versions of the diatonic scale that have the maximum number of consonant triads available, then it turns out all of these scales will be 7-note subsets of Blackwood[10]. They will also be the most compact arrangement of those five consonant triads possible on the 5-limit triangular lattice, which is just a fancy way of saying those five chords will be maximally connected to each other by common tones. This suggests that one can approach melody in Blackwood[10] by treating it not as one 10-note scale, but as several related 7-note scales, each of which functions like a 5-limit untempered version of the diatonic scale.
This approach allows one to apply the usual principles of diatonic tonality and modality, with the caveat that each familiar mode of the diatonic scale will come in two flavors, depending which of the 7 notes one wants to build consonant triads on. The two flavors will share six notes in common, but one of the seven will differ by 81/80 (i.e. one step of 15edo). Interesting relationships do arise if one maintains the tonic but switches through its different modes (i.e. 1 mixolydian to 1 ionian to 1 lydian), and an "extra" mode appears, because of the fact that 256/243 is tempered out (a way to understand 256/243 vanishing in musical terms is that V/V/V/V = IV, unlike in meantone where V/V/V/V = iii). All together, there are 14 modes of the 7-note diatonic to be found in Blackwood[10] if we keep the same tonic, and 20 if we allow alterations of the tonic.
MODMOSes of Blackwood[10]
Single-alteration MODMOSes
0-160-240-400-480-560-720-880-960-1120-1200
0-80-240-320-480-560-720-800-960-1120-1200
Double-alteration MODMOSes
0-160-240-400-480-560-720-800-960-1120-1200
0-160-240-320-480-560-720-800-960-1120-1200
0-160-240-320-480-640-720-800-960-1120-1200
0-160-240-320-480-640-720-800-960-1040-1200