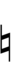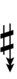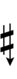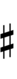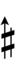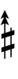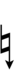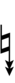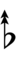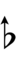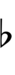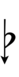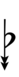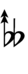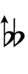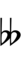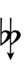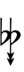User:BudjarnLambeth/272ed23
| This user page is editable by any wiki editor.
As a general rule, most users expect their user space to be edited only by themselves, except for minor edits (e.g. maintenance), undoing obviously harmful edits such as vandalism or disruptive editing, and user talk pages. However, by including this message box, the author of this user page has indicated that this page is open to contributions from other users (e.g. content-related edits). |
| ← 271ed23 | 272ed23 | 273ed23 → |
272 equal divisions of the 23rd harmonic (abbreviated 272ed23) is a nonoctave tuning system that divides the interval of 23/1 into 272 equal parts of about 20 ¢ each. Each step represents a frequency ratio of 231/272, or the 272nd root of 23.
272ed23 is primarily intended to be used as 60edo but with slightly compressed octaves.
Theory
Compared to pure-octaves 60edo, 272ed23 features a relatively large improvement to 7/1 and 11/1, at the cost of moderate worsening of 2/1, 3/1 and 5/1.
It also causes the vals to flip for 5/1, 7/1, 13/1 and 17/1.
These characteristics, particularly the flipped 5/1 and 13/1, are preferred over pure-octaves 60edo for catnip temperament specifically. They change catnip’s warts from 60cf to 272dg (later letters in the alphabet are better).
Given this, 272ed23 can be thought of as a 60edo clone tailor-made for catnip.
60edo is already on the optimal ET sequence for catnip, so 272ed23 is one of the most optimal catnip tunings concievable.
Prime harmonics
In the 47-limit, 272ed3 has less than 40% relative error on primes 2, 3, 5, 7, 11, 17, 23, 29, 31, 37, 41, 43 and 47.
This makes it a solid tuning for the entire no-13, no-19 47-limit.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.59 | -6.05 | +7.65 | +3.89 | -0.28 | +9.86 | +4.44 | -8.51 | +0.00 | -2.17 | +2.12 |
| Relative (%) | -13.0 | -30.3 | +38.3 | +19.5 | -1.4 | +49.4 | +22.2 | -42.6 | +0.0 | -10.8 | +10.6 | |
| Steps (reduced) |
60 (60) |
95 (95) |
140 (140) |
169 (169) |
208 (208) |
223 (223) |
246 (246) |
255 (255) |
272 (0) |
292 (20) |
298 (26) | |
| Harmonic | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -4.84 | -2.94 | -5.57 | +0.09 | -8.33 | +5.57 | +7.73 | +4.96 | +4.35 | -3.83 | -0.88 |
| Relative (%) | -24.2 | -14.7 | -27.9 | +0.5 | -41.8 | +27.9 | +38.7 | +24.8 | +21.8 | -19.2 | -4.4 | |
| Steps (reduced) |
313 (41) |
322 (50) |
326 (54) |
334 (62) |
344 (72) |
354 (82) |
357 (85) |
365 (93) |
370 (98) |
372 (100) |
379 (107) | |
60edo for comparison
In the 47-limit, 60edo has less than 40% relative error on primes 2, 3, 5, 13, 17, 19, 31, 47.
This makes it a solid tuning for the no-7, no-11 19-limit (or dual-7, dual-11).
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -1.96 | -6.31 | -8.83 | +8.68 | -0.53 | -4.96 | +2.49 | -8.27 | -9.58 | -5.04 |
| Relative (%) | +0.0 | -9.8 | -31.6 | -44.1 | +43.4 | -2.6 | -24.8 | +12.4 | -41.4 | -47.9 | -25.2 | |
| Steps (reduced) |
60 (0) |
95 (35) |
139 (19) |
168 (48) |
208 (28) |
222 (42) |
245 (5) |
255 (15) |
271 (31) |
291 (51) |
297 (57) | |
| Harmonic | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +8.66 | -9.06 | +8.48 | -5.51 | +6.50 | +0.83 | +3.12 | +0.69 | +0.30 | -7.79 | -4.54 |
| Relative (%) | +43.3 | -45.3 | +42.4 | -27.5 | +32.5 | +4.1 | +15.6 | +3.5 | +1.5 | -38.9 | -22.7 | |
| Steps (reduced) |
313 (13) |
321 (21) |
326 (26) |
333 (33) |
344 (44) |
353 (53) |
356 (56) |
364 (4) |
369 (9) |
371 (11) |
378 (18) | |
Subsets and supersets
272ed23 is quite composite, with subset ed23s 1, 2, 4, 8, 16, 17, 34, 68, 136.
Unlike pure-octaves 60edo, 272ed23 does not have high consistency at all. 60edo is both consistent and distinctly consistent up to the 9-integer limit, while 272ed23 is consistent and distinctly consistently only up to the 4-integer limit.
Notation
272ed23 can be notated using ups and downs notation using Helmholtz-Ellis accidentals as if it were 60edo:
| Semitones | 0 | 1⁄5 | 2⁄5 | 3⁄5 | 4⁄5 | 1 | 1+1⁄5 | 1+2⁄5 | 1+3⁄5 | 1+4⁄5 | 2 | 2+1⁄5 | 2+2⁄5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sharp symbol | |||||||||||||
| Flat symbol |
If arrows are taken to have their own layer of enharmonic spellings, then in some cases certain notes may be best spelled with three arrows.
Intervals
| Degrees | Cents | Approximate ratios in the 11-limit |
Additional ratios in the no-13, no-19 47-limit |
Additional ratios in the full 47-limit |
|---|---|---|---|---|
| 0 | 0 | 1/1 | ||
| 1 | 19.96 | 55/54, 56/55, 64/63, 81/80 | 51/50, 63/62, 69/68, 70/69, 75/74, 82/81, 85/84, 88/87 | 52/51, 53/52, 57/56, 58/57, 65/64, 66/65, 76/75, 77/76, 78/77 |
| 2 | 39.91 | 33/32, 36/35 | 34/33, 35/34, 37/36, 41/40, 42/41, 43/42, 44/43 | 38/37, 39/38, 40/39 |
| 3 | 59.87 | 25/24, 28/27 | 24/23, 29/28, 30/29, 88/85 | 26/25, 27/26 |
| 4 | 79.83 | 21/20, 22/21 | 23/22, 45/43 | 19/18, 20/19 |
| 5 | 99.78 | 16/5, 35/33 | 17/16, 18/17 | |
| 6 | 119.74 | 15/14 | 29/27, 44/41, 74/69 | 14/13 |
| 7 | 139.70 | 25/23, 51/47 | 13/12, 38/35 | |
| 8 | 159.66 | 11/10, 12/11 | 23/21, 34/31 | 57/52 |
| 9 | 179.61 | 10/9 | 31/28, 41/37, 51/46 | 21/19 |
| 10 | 199.57 | 9/8, 28/25, 55/49 | 37/33, 46/41 | 19/17 |
| 11 | 219.53 | 8/7 (patent) | 17/15, 42/37 | |
| 12 | 239.48 | 8/7 (catnip) | 23/20, 31/27, 54/47, 85/74 | 15/13 |
| 13 | 259.44 | 7/6 | 29/25, 36/31, 43/37 | 22/19 |
| 14 | 279.4 | 20/17, 27/23, 47/40 | 13/11 | |
| 15 | 299.35 | 25/21 | 44/37 | 19/16 |
| 16 | 319.31 | 6/5, 77/64 | 29/24, 35/28, 41/34 | 23/19, 47/39, 65/54 |
| 17 | 339.27 | 11/9 | 17/14, 28/23, 45/37 | |
| 18 | 359.22 | 27/22 | 43/35 | 16/13, 91/74 |
| 19 | 379.18 | 5/4, 56/45 | 21/17, 31/25, 36/29, 41/33, 46/37, 51/41 | 26/21 |
| 20 | 399.14 | 63/50 | 29/23, 34/27 | 19/15, 24/19 |
| 21 | 419.09 | 14/11 | 23/18, 37/29, 51/40 | 65/51 |
| 22 | 439.05 | 9/7 | 22/17, 31/24, 40/31, 58/45 | 49/38 |
| 23 | 459.01 | 176/135 | 30/23, 43/33 | 13/10, 17/13 |
| 24 | 478.97 | 21/16, 33/25 | 29/22, 62/47 | 25/19, 91/69 |
| 25 | 498.92 | 4/3, 75/56 | 43/32, 47/35, 63/47, 99/74 | 39/29, 51/38, 87/65, 91/68 |
| 26 | 518.88 | 27/20 | 23/17, 31/23, 58/43, 85/63 | 19/14 |
| 27 | 538.84 | 15/11 | 41/30, 56/41, 86/63 | 26/19 |
| 28 | 558.79 | 11/8 | 29/21, 40/29, 69/50 | 18/13 |
| 29 | 578.75 | 7/5, 25/18, 88/63 | 32/23, 46/33, 60/43, 81/58 | 39/28, 95/68 |
| 30 | 598.71 | 17/12, 24/17, 41/29 | 65/46 | |
| 31 | 618.66 | 10/7, 63/44 | 23/16, 33/23, 43/30 | 93/65 |
| 32 | 638.62 | 81/56 | 29/20, 42/29, 68/47 | 13/9, 55/38, 94/65 |
| 33 | 658.58 | 16/11, 22/15 | 41/28, 60/41 | 19/13 |
| 34 | 678.53 | 25/17, 31/21, 34/32, 37/25 | 28/19 | |
| 35 | 698.49 | 3/2, 49/33 | 55/37, 64/43, 70/47, 82/55, 94/63 | 52/35, 58/39, 76/51, 85/57 |
| 36 | 718.45 | 32/21, 50/33 | 29/19, 35/23, 41/27, 44/29, 47/31 | 38/25 |
| 37 | 738.40 | 49/32 | 23/15, 72/47 | 20/13, 26/17 |
| 38 | 748.36 | 14/9 | 17/11, 31/20, 48/31 | |
| 39 | 778.32 | 11/7, 25/16 | 36/23, 47/30, 69/44 | |
| 40 | 798.28 | 27/17, 46/29 | 19/12, 65/41 | |
| 41 | 818.23 | 8/5, 45/28, 77/48 | 29/18, 37/23, 69/43 | 21/13 |
| 42 | 838.19 | 34/21, 47/29, 60/37 | 13/8, 21/13 | |
| 43 | 858.15 | 18/11 | 23/14, 41/25 | 64/39 |
| 44 | 878.10 | 5/3, 33/20 | 28/17, 48/29, 58/35, 68/41, 93/56 | 38/23, 43/26, 63/38, 78/47 |
| 45 | 898.06 | 27/16, 42/25 | 37/22, 47/28 | 32/19 |
| 46 | 918.02 | 56/33 | 17/10 | 22/13, 39/23 |
| 47 | 937.97 | 12/7, 55/32 | 31/18, 43/25 | 19/11, 98/57 |
| 48 | 958.93 | 7/4 (catnip) | 19/11, 40/23 | 26/15, 33/19 |
| 49 | 977.89 | 7/4 (patent), 44/25 | 30/17, 37/21, 51/29 | 23/13, 95/54 |
| 50 | 997.84 | 16/9, 25/14 | 41/23 | 57/32 |
| 51 | 1017.8 | 9/5 | 29/16, 56/31, 74/41, 92/51 | 38/21, 47/26, 65/36 |
| 52 | 1037.76 | 20/11 | 31/17, 51/28 | |
| 53 | 1057.72 | 11/6 | 94/51 | 24/13, 35/18 |
| 54 | 1077.67 | 28/15 | 41/22, 54/29 | 13/7, 95/51 |
| 55 | 1097.63 | 15/8, 66/35 | 17/9, 32/17 | 49/26 |
| 56 | 1117.59 | 21/11, 40/21 | 82/43 | 19/10 |
| 57 | 1137.54 | 27/14 | 23/12, 29/15, 56/29 | 25/3 |
| 58 | 1157.50 | 35/18 | 31/16, 33/17, 41/21, 80/41 | 37/19, 39/20 |
| 59 | 1177.46 | 49/25, 55/28, 63/32 | 47/24, 57/29, 69/35 | 51/26, 65/33, 75/38, 77/39 |
| 60 | 1200 | 2/1, 99/50 |
Regular temperament properties
Rank-2 temperaments
| Periods per 8ve |
Generator* | Cents* | Associated ratio* |
Temperament |
|---|---|---|---|---|
| 12 | 12\272ed23 (2\272ed23) |
239.48 (39.91) |
8/7 (36/35) |
Catnip (272dg) |
* Octave-reduced form, reduced to the first half-octave, and minimal form in parentheses if distinct
(This table is incomplete.)
Scales
- 60edo scales
These are useable in 272ed23, simply apply an octave compression of 0.99784 in Scale Workshop.
Nearby equal-step tunings
There are a few other useful equal-step tunings which occur close to 272ed23 in step size:
- 207ed11, 168ed7
The tunings 207ed11 and 168ed7 are almost identical. Each is 60edo but with slightly stretched octaves.
Each causes relatively large improvement to 5/1, 7/1 and 11/1 at the cost of moderate worsening of 2/1 and 3/1.
Each also causes the vals to flip for 11/1 and 13/1.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.28 | +3.24 | +1.29 | +0.36 | +0.00 | -8.44 | +8.44 | -3.63 | +6.54 | +6.33 | -8.85 |
| Relative (%) | +16.4 | +16.2 | +6.4 | +1.8 | +0.0 | -42.1 | +42.1 | -18.1 | +32.6 | +31.6 | -44.1 | |
| Steps (reduced) |
60 (60) |
95 (95) |
139 (139) |
168 (168) |
207 (0) |
221 (14) |
245 (38) |
254 (47) |
271 (64) |
291 (84) |
296 (89) | |
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +3.15 | +3.04 | +0.99 | +0.00 | -0.44 | -8.92 | +7.92 | -4.17 | +5.96 | +5.71 | -9.49 |
| Relative (%) | +15.7 | +15.1 | +4.9 | +0.0 | -2.2 | -44.5 | +39.5 | -20.8 | +29.7 | +28.5 | -47.3 | |
| Steps (reduced) |
60 (60) |
95 (95) |
139 (139) |
168 (0) |
207 (39) |
221 (53) |
245 (77) |
254 (86) |
271 (103) |
291 (123) |
296 (128) | |
- 301zpi
The tuning 301zpi, the 301st zeta peak index, is 60edo but with slightly stretched octaves.
It causes relatively large improvement to 3/1, 5/1, 7/1, 11/1 and 17/1 at the cost of relatively small worsening of 2/1 and relatively large worsening of 13/1.
It also causes the val for 11/1 to flip from 208 steps to 207 steps.
301zpi is both consistent and distinctly consistent up to the 10-integer-limit, which is unusually high for a two digit edo or three digit zpi.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +1.60 | +0.58 | -2.61 | -4.35 | -5.80 | +5.39 | +1.57 | +9.28 | -1.05 | -1.82 | +2.88 |
| Relative (%) | +8.0 | +2.9 | -13.0 | -21.7 | -29.0 | +26.9 | +7.9 | +46.3 | -5.3 | -9.1 | +14.4 | |
| Step | 60 | 95 | 139 | 168 | 207 | 222 | 245 | 255 | 271 | 291 | 297 | |
- 60edo
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | +0.00 | -1.96 | -6.31 | -8.83 | +8.68 | -0.53 | -4.96 | +2.49 | -8.27 | -9.58 | -5.04 |
| Relative (%) | +0.0 | -9.8 | -31.6 | -44.1 | +43.4 | -2.6 | -24.8 | +12.4 | -41.4 | -47.9 | -25.2 | |
| Steps (reduced) |
60 (0) |
95 (35) |
139 (19) |
168 (48) |
208 (28) |
222 (42) |
245 (5) |
255 (15) |
271 (31) |
291 (51) |
297 (57) | |
- 255ed19
The tuning 255ed19 is 60edo but with slightly compressed octaves.
It causes a relatively large improvement to 11/1, at the cost of relatively small worsening of every smaller prime.
It also causes the val for 7/1 to flip from 168 steps to 169.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -0.59 | -2.88 | -7.67 | +9.53 | +6.65 | -2.69 | -7.34 | +0.00 | +9.07 | +7.57 | -7.93 |
| Relative (%) | -2.9 | -14.4 | -38.4 | +47.7 | +33.3 | -13.5 | -36.7 | +0.0 | +45.4 | +37.9 | -39.7 | |
| Steps (reduced) |
60 (60) |
95 (95) |
139 (139) |
169 (169) |
208 (208) |
222 (222) |
245 (245) |
255 (0) |
272 (17) |
292 (37) |
297 (42) | |
- 208ed11
The tuning 208ed11 is 60edo but with slightly compressed octaves.
It causes a relatively large improvement to 7/1 and 11/1, at the cost of moderate worsening of 2/1, 3/1 and 5/1.
It also causes the vals to flip for 5/1, 7/1 and 17/1.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.50 | -5.92 | +7.84 | +4.12 | +0.00 | -9.79 | +4.78 | -8.16 | +0.37 | -1.77 | +2.53 |
| Relative (%) | -12.5 | -29.7 | +39.3 | +20.6 | +0.0 | -49.1 | +23.9 | -40.9 | +1.9 | -8.8 | +12.7 | |
| Steps (reduced) |
60 (60) |
95 (95) |
140 (140) |
169 (169) |
208 (0) |
222 (14) |
246 (38) |
255 (47) |
272 (64) |
292 (84) |
298 (90) | |
- 272ed23
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | -2.59 | -6.05 | +7.65 | +3.89 | -0.28 | +9.86 | +4.44 | -8.51 | +0.00 | -2.17 | +2.12 |
| Relative (%) | -13.0 | -30.3 | +38.3 | +19.5 | -1.4 | +49.4 | +22.2 | -42.6 | +0.0 | -10.8 | +10.6 | |
| Steps (reduced) |
60 (60) |
95 (95) |
140 (140) |
169 (169) |
208 (208) |
223 (223) |
246 (246) |
255 (255) |
272 (0) |
292 (20) |
298 (26) | |
Instruments
Due to 60edo's highly composite nature, 272ed23 has an unusually high number of ways it can be subdivided. This means it has multiple good skip-fretting systems which can be used to create stringed instruments with playable fret spacings that still span the full gamut. Probably the best of these is tuning a compressed-octaves 20edo guitar to major thirds, emulating the pure-octaves one by Robin Perry in the image below. This is very closely related to the Kite Guitar.