Uniform map

A uniform map is any map found by uniformly multiplying every entry of the just intonation point (JIP) for some prime limit [math]\displaystyle{ p }[/math], ⟨log₂2 log₂3 log₂5 ... log₂[math]\displaystyle{ p }[/math]], by the same positive real number before rounding them to integers.

This visualizes EDO maps. We could call it the uniform map continuum. Generator size decreases to the right, so the EDO number goes up. Each colored cell is the closest approximation of steps to a prime for that generator size. We can see uniform maps as any set of step counts for primes found as perfectly vertical lines drawn through such a diagram. And integer uniform maps would be any such vertical line that is also drawn straight through a number which appears in the row for n-ED2.

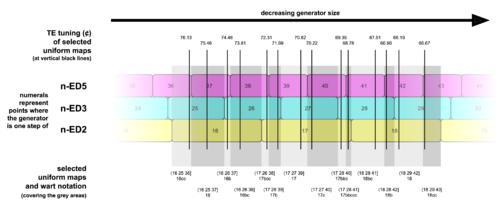
What this means is that somewhere along the continuum of all possible equal-step tuning generator sizes, we can find one whose individually closest approximations for each of the primes is given by this map. In this sense, uniform maps are those that give reasonable tunings (further discussion of this idea may be found here). The map with the overall best tuning accuracy for an EDO will always be a uniform map. In many regular temperament theory contexts, uniform maps are the only maps used, such as in the famous projective tuning space diagrams from Paul Erlich's seminal A Middle Path paper, or the optimal GPV sequences given for many regular temperaments across the wiki.

For an example, choosing 17.1 as our uniform multiplier, we find the map 17.1·⟨log₂2 log₂3 log₂5] = ⟨17.1 27.103 39.705] which rounds to ⟨17 27 40]. This is one of the many uniform maps for 17-EDO.

Every EDO has a finite number of possible uniform maps within a given prime limit, but an infinite number of uniform maps if no prime limit is given.

To find a uniform map for some [math]\displaystyle{ n }[/math]-EDO, choose any multiplier that rounds to [math]\displaystyle{ n }[/math] (anywhere from [math]\displaystyle{ n - 0.5 }[/math] to [math]\displaystyle{ n + 0.5 }[/math]). For example, 16.9 rounds to 17, so we could use that to find another example for 17-EDO. Uniformly multiplying 16.9·⟨log₂2 log₂3 log₂5] = ⟨16.9 26.786 39.241], which rounds to ⟨17 27 39].

Subgroup uniform maps are also possible. For example, a uniform map on the 2.5.9/7 subgroup would be found by uniformly multiplying ⟨log₂2 log₂5 log₂(9/7)].

Integer uniform map

A uniform map whose multiplier is an integer is called an integer uniform map, or simple map. For example, we could use the integer 17 itself directly. So 17·⟨log₂2 log₂3 log₂5] = ⟨17 26.944 39.473], which also rounds to ⟨17 27 39].

Vs. related terminology

A uniform map is the same thing as a generalized patent val, or GPV.

An integer uniform map is the same thing as a patent val.

As for the difference between "map" and "val", there is none, at least in most RTT cases; this is discussed here: Map.

Otherwise, the difference in terminology between uniform maps, integer uniform maps, patent vals, and GPVs, reflects an inversion in conceptual framing. For patent vals and GPVs, patent vals are considered the base case, and GPVs a generalization thereof, whereas for uniform maps and integer uniform maps, uniform maps are considered the base case and integer uniform maps a specialization thereof. There is an argument that uniform maps are the more fundamental and important concept to regular temperament theory and therefore that this framing is the superior of the two.