|
|
| Line 1: |
Line 1: |
| <span style="color: #0000ff; font-family: Arial; font-size: 13.3333px;"><span style="font-family: arial,sans-serif;"><span style="font-family: arial,sans-serif;">'''<span style="color: #000000;">Equal divisions of length</span>'''</span></span></span>
| | ==Equal divisions of length== |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">For an intervallic system with n divisions , </span>[http://sites.google.com/site/240edo/equaldivisionsoflength%28edl%29 **EDL**]<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> is <span style="font-family: arial,sans-serif;">considered as equal divisions of length</span> by dividing string length to</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> n</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> equal divisions ( So , we have '''n/2''' divisions per octave).If the first division is </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">L1</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> and the last, </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">Ln</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> , we have: </span></span>
| | For an intervallic system with n divisions , [http://sites.google.com/site/240edo/equaldivisionsoflength%28edl%29 EDL] is considered as equal divisions of length by dividing string length to '''n''' equal divisions (so, we have '''n/2''' divisions per octave). If the first division is '''L1''' and the last, '''Ln''', we have: |
|
| |
|
| <span style="text-align: left;">'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">L1 = L2 = L3 = …… = Ln</span>'''</span>
| | :: L1 = L2 = L3 = ... = Ln |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">So sum of the divisions is </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">L</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> or the string length. Note that the number of divisions in octave is half of the string length.By dividing string length of </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">L</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> to </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">n</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> division we have: </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">n : n-1 : n-2 : n-3 : ……. : n-m : ….. : n-n </span>'''</span>
| | So sum of the divisions is '''L''' or the string length. Note that the number of divisions in octave is half of the string length. By dividing string length of '''L''' to '''n''' division we have: |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> which </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">n-m </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">is </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">n/2.</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> for example, by dividing string length to 12 equal divisions we have a series as:</span></span>
| | :: n : n-1 : n-2 : n-3 : ... : n-m : ... : n-n |
|
| |
|
| <span style="text-align: left;">'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">12:11:10:9:8:7:6:5:4:3:2:1:0</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> or </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">12 11 10 9 8 7 6 5 4 3 2 1 0 </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">which shows </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">12-EDL</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">:</span></span>
| | where '''n-m''' is '''n/2'''. |
|
| |
|
| <span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> </span>
| |
|
| |
|
| <div class='external-image-warning' style='background-color:#f8f9fa; border: 1px solid #eaecf0; padding-left: 0.5em; padding-right:0.5em; display:inline-block'>
| | For example, by dividing string length to 12 equal divisions we have a series as: |
| External image: http://sites.google.com/site/240edo/edl1-custom-size-381-249.jpg<br>
| |
| : <small><b>WARNING</b>: MediaWiki doesn't have very good support for external images.</small><br>
| |
| : <small>Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.</small>
| |
| </div>
| |
| [[Category:IMPORTDEBUG - Change External Images]]
| |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">'''12:12''' means 12 from 12 divisions,'''12:11''' means 11 from 12 divisions and so on.Ratios as '''12:11''' shows active string length for each degree, which is vibrating.'''EDL''' system shows ascending trend of divisions sizes due to its inner structure and if compared with </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">EDO</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> :</span></span>
| | :: 12:11:10:9:8:7:6:5:4:3:2:1:0 or 12 11 10 9 8 7 6 5 4 3 2 1 0 |
|
| |
|
| <span style="display: block; text-align: center;">
| | which shows '''12-EDL''': |
|
| |
|
| </span>
| | [[file:edl1.jpg]] |
|
| |
|
| <div class='external-image-warning' style='background-color:#f8f9fa; border: 1px solid #eaecf0; padding-left: 0.5em; padding-right:0.5em; display:inline-block'>
| | '''12:12''' means 12 from 12 divisions, '''12:11''' means 11 from 12 divisions and so on. Ratios as 12:11 shows active string length for each degree, which is vibrating. EDL system shows ascending trend of divisions sizes due to its inner structure and if compared with [[EDO]]: |
| External image: http://sites.google.com/site/240edo/edl2.JPG<br>
| |
| : <small><b>WARNING</b>: MediaWiki doesn't have very good support for external images.</small><br> | |
| : <small>Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.</small>
| |
| </div>
| |
| [[Category:IMPORTDEBUG - Change External Images]] | |
|
| |
|
| <span style="display: block; text-align: center;"><span style="color: #000000; font-family: Arial; font-size: 14.6667px;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> </span></span>
| | [[file:Edl2.JPG]] |
|
| |
|
| <span style="text-align: center;"><span style="color: #000000; font-family: Arial; font-size: 14.6667px;">'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"><u>Relation between Utonality and EDL system</u></span>'''</span></span>
| | ==Relation between Utonality and EDL system== |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">We can consider </span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">EDL</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> system as </span><span style="color: #0000ff; font-family: Arial; font-size: 13.3333px;">[http://en.wikipedia.org/wiki/Otonal **Utonal system**]</span><span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> .</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;">Utonality</span>'''<span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> is a term introduced by </span><span style="color: #0000ff; font-family: Arial; font-size: 13.3333px;">[http://en.wikipedia.org/wiki/Harry_Partch **Harry Partch**]</span><span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> to describe chords whose notes are the "undertones" (divisors) of a given fixed tone.</span></span>
| | We can consider EDL system as [http://en.wikipedia.org/wiki/Otonal Utonal system]. '''Utonality''' is a term introduced by [http://en.wikipedia.org/wiki/Harry_Partch Harry Partch] to describe chords whose notes are the "undertones" (divisors) of a given fixed tone. |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">In the other hand , an utonality is a collection of pitches which can be expressedin ratios that have the same nominators. For example, 7/4, 7/5, 7/6 form an utonality which 7 as nominator is called "</span><span style="color: #0000ff; font-family: Arial; font-size: 13.3333px;">[http://tonalsoft.com/enc/n/nexus.aspx **Numerary nexus**]</span><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">".</span></span>
| | In the other hand, a utonality is a collection of pitches which can be expressed in ratios that have the same numerators. For example, 7/4, 7/5, 7/6 form an utonality which 7 as numerator is called "[http://tonalsoft.com/enc/n/nexus.aspx Numerary nexus]". |
|
| |
|
| <span style="text-align: left;"><span style="color: #000000; font-family: Arial; font-size: 13.3333px;">If a string is divided into equal parts, it will produce an utonality and so we have EDL system.EDL systems are classified as systems with unequal </span><span style="color: #0000ff; font-family: Arial; font-size: 13.3333px;">[http://tonalsoft.com/enc/e/epimorios.aspx **epimorios**]</span><span style="color: #000000; font-family: Arial; font-size: 13.3333px;"> '''('''[http://en.wikipedia.org/wiki/Superparticular_number **Superparticular**]''')''' divisions which show descending series with ascending sizes.</span></span>
| | If a string is divided into equal parts, it will produce an utonality and so we have EDL system. EDL systems are classified as systems with unequal [http://tonalsoft.com/enc/e/epimorios.aspx epimorios]([http://en.wikipedia.org/wiki/Superparticular_number Superparticular]) divisions which show descending series with ascending sizes. |
|
| |
|
| </span> [[Category:edl]]
| | [[Category:edl]] |
Equal divisions of length
For an intervallic system with n divisions , EDL is considered as equal divisions of length by dividing string length to n equal divisions (so, we have n/2 divisions per octave). If the first division is L1 and the last, Ln, we have:
- L1 = L2 = L3 = ... = Ln
So sum of the divisions is L or the string length. Note that the number of divisions in octave is half of the string length. By dividing string length of L to n division we have:
- n : n-1 : n-2 : n-3 : ... : n-m : ... : n-n
where n-m is n/2.
For example, by dividing string length to 12 equal divisions we have a series as:
- 12:11:10:9:8:7:6:5:4:3:2:1:0 or 12 11 10 9 8 7 6 5 4 3 2 1 0
which shows 12-EDL:
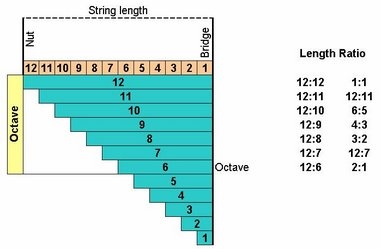
12:12 means 12 from 12 divisions, 12:11 means 11 from 12 divisions and so on. Ratios as 12:11 shows active string length for each degree, which is vibrating. EDL system shows ascending trend of divisions sizes due to its inner structure and if compared with EDO:
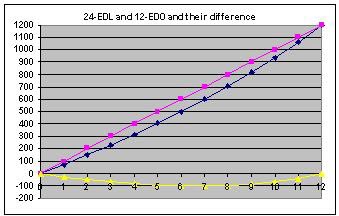
Relation between Utonality and EDL system
We can consider EDL system as Utonal system. Utonality is a term introduced by Harry Partch to describe chords whose notes are the "undertones" (divisors) of a given fixed tone.
In the other hand, a utonality is a collection of pitches which can be expressed in ratios that have the same numerators. For example, 7/4, 7/5, 7/6 form an utonality which 7 as numerator is called "Numerary nexus".
If a string is divided into equal parts, it will produce an utonality and so we have EDL system. EDL systems are classified as systems with unequal epimorios(Superparticular) divisions which show descending series with ascending sizes.

