User:Nick Vuci/Moments of Symmetry: Difference between revisions
Jump to navigation
Jump to search
added intro |
m Small typo on image captions Tags: Visual edit Mobile edit Mobile web edit |
||
| Line 4: | Line 4: | ||
== Constructing Moments of Symmetry == | == Constructing Moments of Symmetry == | ||
<gallery mode="nolines" widths="200" heights="200"> | <gallery mode="nolines" widths="200" heights="200"> | ||
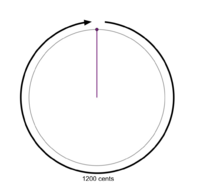
File:1-1 MOS Construction.png|An interval is chosen to be the period (the 1200 cent octave in this example). | File:1-1 MOS Construction.png|An interval is chosen to be the period (the 1200 cent octave in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise. | ||
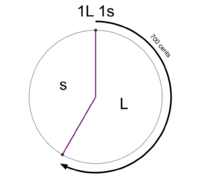
File:1-2 MOS Construction.png|An interval is chosen to be a generator (the 700 cent perfect fifth in this example). This is the 1L 2s MOS pattern. | File:1-2 MOS Construction.png|An interval is chosen to be a generator (the 700 cent perfect fifth in this example). This is the 1L 2s MOS pattern. | ||
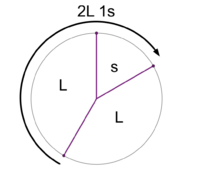
File:1-3 MOS Construction.png|Stacking the generator upon itself yields a scale with 2 step sizes This is the 2L 1s MOS pattern. | File:1-3 MOS Construction.png|Stacking the generator upon itself yields a scale with 2 step sizes. This is the 2L 1s MOS pattern. | ||
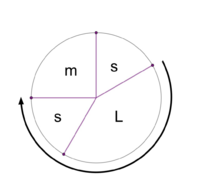
File:1-4 MOS Construction.png|Stacking the generator 2 times yields a scale with 3 step sizes (not MOS). | File:1-4 MOS Construction.png|Stacking the generator 2 times yields a scale with 3 step sizes (not MOS). | ||
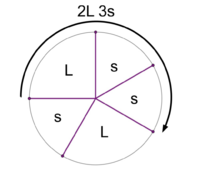
File:1-5 MOS Construction.png|Stacking the generator 3 times yields a scale with 2 step sizes. This is the 2L 3s MOS pattern. | File:1-5 MOS Construction.png|Stacking the generator 3 times yields a scale with 2 step sizes. This is the 2L 3s MOS pattern. | ||
Revision as of 18:32, 27 May 2025
WORK-IN-PROGRESS AS OF 27 MAY 2025
Moments of Symmetry (MOS) are scales created by a simple procedure that generates the common pentatonic and diatonic scales, but also extends their melodic coherence and structural balance to a wide range of novel xenharmonic scales. First described by Erv Wilson in the 1970's, the concept shares fundamental similarities and is often though of as synonymous with the concept of Well-Formed scales, as well as the more generalized concept of MV2 scales. Over time, MOS has become a central tool in xenharmonic theory, inspiring a wide range of musical uses, analytical approaches, and derivative concepts such as MODMOS, multi-MOS, and MOS-based rhythm.
Constructing Moments of Symmetry
-
An interval is chosen to be the period (the 1200 cent octave in this example). The period is represented with a circle; intervals are represented with purple lines and points radiating out from the middle which move clockwise.
-
An interval is chosen to be a generator (the 700 cent perfect fifth in this example). This is the 1L 2s MOS pattern.
-
Stacking the generator upon itself yields a scale with 2 step sizes. This is the 2L 1s MOS pattern.
-
Stacking the generator 2 times yields a scale with 3 step sizes (not MOS).
-
Stacking the generator 3 times yields a scale with 2 step sizes. This is the 2L 3s MOS pattern.
-
Stacking the generator five times yields a scale with three step sizes (not MOS).
-
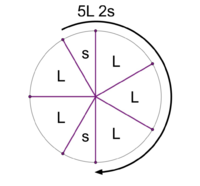
Stacking the generator 6 times yields a scale with 2 step sizes. This is the 5L 2s MOS pattern.