Uniform map: Difference between revisions
Cmloegcmluin (talk | contribs) Created page with "A '''uniform map''' is any near-just map found by ''uniformly'' multiplying every entry of the just intonation point (JIP) {{map|log₂2 log₂3 log₂5 ...}} by some..." |
Cmloegcmluin (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
A '''uniform map''' is any near-just [[map]] found by ''uniformly'' multiplying every entry of the [[just intonation point]] (JIP) {{map|log₂2 log₂3 log₂5 ...}} by some value before rounding it to integers. | A '''uniform map''' is any near-just [[map]] found by ''uniformly'' multiplying every entry of the [[just intonation point]] (JIP) {{map|log₂2 log₂3 log₂5 ...}} by some value before rounding it to integers. | ||
[[File:Near_linings_up_rare2.png|thumb|right|500px|This visualizes | [[File:Near_linings_up_rare2.png|thumb|right|500px|This visualizes EDO maps. We could call it the uniform map continuum. Generator size decreases to the right, so the EDO number goes up. Each colored cell is the closest approximation of steps to a prime for that generator size. We can see uniform maps as any set of step counts for primes found as perfectly vertical lines drawn through such a diagram. And integer uniform maps would be any such vertical line that is also drawn straight through a number which appears in the row for n-ED2.]] | ||
What this means is that somewhere along the continuum of all possible [[equal-step tuning]] [[generator]] sizes, we can find one whose individually closest approximations for each of the primes is given by this map. In this sense, uniform maps are those that give reasonable tunings (further discussion of this idea may be found [[Patent_val#Generalized_patent_val|here]]). The map with the overall best tuning accuracy for an EDO will always be a uniform map. In many [[regular temperament theory]] contexts, uniform maps are the only maps used, such as in the famous [[projective tuning space]] diagrams from [[Paul Erlich]]'s seminal A Middle Path paper, or the [[optimal GPV sequence]]s given for many [[regular temperament]]s across the wiki. | |||
To find a uniform map for n- | For an example, choosing 17.1 as our uniform multiplier, we find the map 17.1·{{map|log₂2 log₂3 log₂5}} = {{map|17.1 27.103 39.705}} which rounds to {{map|17 27 40}}. This is one of the many uniform maps for 17-EDO, and every [[EDO]] has many possible uniform maps. | ||
To find a uniform map for some <math>n</math>-EDO, choose any multiplier that rounds to <math>n</math>. For example, 16.9 rounds to 17, so we could use that to find another example for 17-EDO. Uniformly multiplying 16.9·{{map|log₂2 log₂3 log₂5}} = {{map|16.9 26.786 39.241}}, which rounds to {{map|17 27 39}}. To find all uniform maps for <math>n</math>-EDO, check ''every'' multiplier that rounds to <math>n</math>, i.e. every multiplier from <math>n - 0.5</math> to <math>n + 0.5</math>. For a more mathematical approach to finding many uniform maps, see: [[Patent val/Properties]]. | |||
== Integer uniform map == | == Integer uniform map == | ||
A uniform map whose multiplier is an integer is called an '''integer uniform map'''. For example, we could use the integer 17 itself directly. So | A uniform map whose multiplier is an integer is called an '''integer uniform map'''. For example, we could use the integer 17 itself directly. So 17·{{map|log₂2 log₂3 log₂5}} = {{map|17 26.944 39.473}}, which also rounds to {{map|17 27 39}}. | ||
== Vs. related terminology == | == Vs. related terminology == | ||
| Line 21: | Line 17: | ||
A uniform map is the same thing as a [[generalized patent val]], or GPV. | A uniform map is the same thing as a [[generalized patent val]], or GPV. | ||
An integer uniform map | An integer uniform map is the same thing as a [[simple map]], or [[patent val]]. | ||
As for the difference between "map" and "val", there is none, at least in most [[RTT]] cases; this is discussed here: [[Val#Vals_vs._mappings]]. | |||
Otherwise, the difference in terminology between uniform maps, integer uniform maps, patent vals, and GPVs, reflects an inversion in conceptual framing. For patent vals and GPVs, patent vals are considered the base case, and GPVs a generalization thereof, whereas for uniform maps and integer uniform maps, uniform maps are considered the base case and integer uniform maps a specification thereof. | Otherwise, the difference in terminology between uniform maps, integer uniform maps, patent vals, and GPVs, reflects an inversion in conceptual framing. For patent vals and GPVs, patent vals are considered the base case, and GPVs a generalization thereof, whereas for uniform maps and integer uniform maps, uniform maps are considered the base case and integer uniform maps a specification thereof. There is an argument that uniform maps are the more fundamental and important concept to regular temperament theory and therefore that this framing is the superior of the two. | ||
[[Category:Temperament]] | [[Category:Temperament]] | ||
Revision as of 22:27, 12 December 2021
A uniform map is any near-just map found by uniformly multiplying every entry of the just intonation point (JIP) ⟨log₂2 log₂3 log₂5 ...] by some value before rounding it to integers.
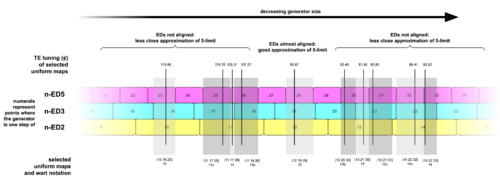
What this means is that somewhere along the continuum of all possible equal-step tuning generator sizes, we can find one whose individually closest approximations for each of the primes is given by this map. In this sense, uniform maps are those that give reasonable tunings (further discussion of this idea may be found here). The map with the overall best tuning accuracy for an EDO will always be a uniform map. In many regular temperament theory contexts, uniform maps are the only maps used, such as in the famous projective tuning space diagrams from Paul Erlich's seminal A Middle Path paper, or the optimal GPV sequences given for many regular temperaments across the wiki.
For an example, choosing 17.1 as our uniform multiplier, we find the map 17.1·⟨log₂2 log₂3 log₂5] = ⟨17.1 27.103 39.705] which rounds to ⟨17 27 40]. This is one of the many uniform maps for 17-EDO, and every EDO has many possible uniform maps.
To find a uniform map for some [math]\displaystyle{ n }[/math]-EDO, choose any multiplier that rounds to [math]\displaystyle{ n }[/math]. For example, 16.9 rounds to 17, so we could use that to find another example for 17-EDO. Uniformly multiplying 16.9·⟨log₂2 log₂3 log₂5] = ⟨16.9 26.786 39.241], which rounds to ⟨17 27 39]. To find all uniform maps for [math]\displaystyle{ n }[/math]-EDO, check every multiplier that rounds to [math]\displaystyle{ n }[/math], i.e. every multiplier from [math]\displaystyle{ n - 0.5 }[/math] to [math]\displaystyle{ n + 0.5 }[/math]. For a more mathematical approach to finding many uniform maps, see: Patent val/Properties.
Integer uniform map
A uniform map whose multiplier is an integer is called an integer uniform map. For example, we could use the integer 17 itself directly. So 17·⟨log₂2 log₂3 log₂5] = ⟨17 26.944 39.473], which also rounds to ⟨17 27 39].
A uniform map is the same thing as a generalized patent val, or GPV.
An integer uniform map is the same thing as a simple map, or patent val.
As for the difference between "map" and "val", there is none, at least in most RTT cases; this is discussed here: Val#Vals_vs._mappings.
Otherwise, the difference in terminology between uniform maps, integer uniform maps, patent vals, and GPVs, reflects an inversion in conceptual framing. For patent vals and GPVs, patent vals are considered the base case, and GPVs a generalization thereof, whereas for uniform maps and integer uniform maps, uniform maps are considered the base case and integer uniform maps a specification thereof. There is an argument that uniform maps are the more fundamental and important concept to regular temperament theory and therefore that this framing is the superior of the two.