|
|
| Line 1: |
Line 1: |
| <span style="color: #000000; font-family: arial,sans-serif; font-size: 18px;">'''Arithmetic irrational divisions'''</span>
| | ==Arithmetic irrational divisions== |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">For an intervallic system with </span><u><span style="color: black; font-size: 11pt;">n</span></u><span style="color: black; font-size: 11pt;"> divisions , </span><span style="color: #be00ff; font-size: 11pt;">[http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 AID_]</span><span style="color: black; font-size: 11pt;"> is considered as [http://www.richland.edu/james/lecture/m116/sequences/arithmetic.html arithmetic sequence] with divisions of system as terms of sequence. </span></span>
| | For an intervallic system with <u>n</u> divisions, [http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 AID] is considered as [http://www.richland.edu/james/lecture/m116/sequences/arithmetic.html arithmetic sequence] with divisions of system as terms of sequence. |
|
| |
|
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; text-align: left;"><span style="color: black; font-size: 11pt;"> If the first division is </span><u><span style="color: black; font-size: 11pt;">A1</span></u><span style="color: black; font-size: 11pt;"> and the last , </span><u><span style="color: black; font-size: 11pt;">An</span></u><span style="color: black; font-size: 11pt;"> , with common difference of </span><u><span style="color: black; font-size: 11pt;">d</span></u><span style="color: black; font-size: 11pt;"> , we have : </span></span>
| | If the first division is <u>A1</u> and the last , <u>An</u> , with common difference of <u>d</u> , we have : |
| | :: A1 = A1 |
| | :: A2 = A1+d |
| | :: A3 = A1+2d |
| | :: A4 = A1+3d |
| | :: ... |
| | :: An = A1+(n-1)d |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">A1 = A1</span> | | So sum of the divisions is <u>Sn</u> : |
| | :: '''Sn =( <u>n[2A1+(n-1)d])/2</u>''' |
|
| |
|
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A2 = A1+d </span>
| |
|
| |
|
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A3= A1+2d </span> | | As we can consider <u>Sn</u> of system to be 1200 cent or anything else (octavic or non-octavic system ) then <u>d</u> is most important to make an AID with n divisions with A1. So, the common difference between divisions is : |
| | :: '''d =( <u>2(Sn - nA1))/((n(n-1))</u>''' |
|
| |
|
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">A4 = A1+3d</span>
| | By considering Sn=1200 , A1=70 , n=12 , d will be 5.454545455 and our 12-tone scale is equal to: |
| | :: '''0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0''' |
|
| |
|
| <span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;">……… </span>
| |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;">An = A1+(n-1)d</span> | | Scales based on AID can be subsets of EDO if: |
| | # we choose d=0 so , A1 = Sn/n .. Consider <u>n</u>=8 and <u>A1</u>=150 , then we have 8-EDO . |
| | # for a constant <u>n</u> and different <u>A1</u>, if <u>d</u> and (Sn/A1) are integers, we have a subset of EDO or EDI (Equal divisions of Interval). |
|
| |
|
| <span style="direction: ltr; font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;">So sum of the divisions is </span><u><span style="color: black; font-size: 11pt;">Sn</span></u><span style="color: black; font-size: 11pt;"> :</span></span> | | Consider <u>Sn = 1400</u> , <u>n</u>=8 and <u>A1</u>=70 , then we have a subset of a 140-ED (1400.) with Degrees as 7 17 30 46 65 87 112 140 : |
| | :: 0.0 70.0 170.0 300.0 460.0 650.0 870.0 1120.0 1400.0 |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;">'''<span style="color: black; font-size: 11pt;">Sn =( <u>n[2A1+(n-1)d])/2</u></span>'''</span>
| | And now for Sn=1400 and n=8, |
| | * If A1=175.0 then we have 8-AID(1400.) |
| | * If A1=56 then we have 700-AID(1400.) with Degrees as 28 73 135 214 310 423 553 700 |
| | * If A1=87.5 then we have 112-AID(1400.) with Degrees as 7 16 27 40 55 72 91 112 |
|
| |
|
| <span style="direction: ltr; display: block; text-align: left;"><span style="font-family: Tahoma,Geneva,sans-serif;"><span style="color: black; font-size: 11pt;"> As we can consider </span><u><span style="color: black; font-size: 11pt;">Sn</span></u><span style="color: black; font-size: 11pt;"> of system to be 1200 cent or anything else (octavic or non-octavic system ) then </span><u><span style="color: black; font-size: 11pt;">d</span></u><span style="color: black; font-size: 11pt;"> is most important to make an AID with n divisions with A1.</span></span><span style="color: black; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt;"> So, the common difference between divisions is : </span></span>
| | AID system shows different ascending, descending or linear trend of change in divisions sizes due to relation between n and A1 in AID and EDO with equal degree: |
| | * If choosing <u>A1</u> greater than division size in equal degree EDO , <u>d</u> is negative and <u>AID</u> is descending. |
| | * If choosing <u>A1</u> smaller than division size in equal degree EDO , <u>d</u> is positive and <u>AID</u> is ascending. |
| | * If choosing <u>A1</u> equal to division size in equal degree EDO , <u>d</u> is zero. |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: center;">'''<span style="color: black; font-size: 11pt;">d =( <u>2(Sn - nA1))/((n(n-1))</u></span>'''</span>
| | [[file:AIDO-custom-size-298-402.jpg]] |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">By considering Sn=1200 , A1=70 , n=12 , d will be 5.454545455 and our 12-tone scale is equal to:</span>
| |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;"> '''0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0'''</span>
| | 171.4285714 is point of intersection in these 3 trends: |
|
| |
|
| <span style="color: black; direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 11pt; text-align: left;">Scales based on AID can be subsets of EDO if :</span><span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">1- we choose d=0 so ,<span style="color: black; font-size: 11pt;"> A1 = Sn/n</span> .. Consider </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;">=8 and </span><u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;">=150 , then we have 8-EDO .</span></span>
| | [[file:AIDO2.jpg]] |
|
| |
|
| <span style="direction: ltr; display: block; font-family: Tahoma,Geneva,sans-serif; margin: 0cm 0cm 0pt; text-align: left;"><span style="color: black; font-size: 10pt;">2- for a constant </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;"> and different <u>A1</u>, if <u>d</u> and (Sn/A1) are Integer number , we have a susbet of EDO or EDI( Equal divisions of Interval) .Consider <u>Sn = 1400</u> , </span><u><span style="color: black; font-size: 10pt;">n</span></u><span style="color: black; font-size: 10pt;">=8 and </span><u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;">=70 , then we have a subset of a 140-ED(1400.) with Degrees as 7 17 30 46 65 87 112 140 :</span></span>
| |
|
| |
|
| '''0.000 70.000 170.000 300.000 460.000 650.000 870.000 1120.000 1400.000'''
| | We can have different kinds of AID: |
|
| |
|
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif;">And now for </span><span style="font-family: Tahoma,Geneva,sans-serif;">Sn=1400 and n=8,</span>
| | * AIDO = Arithmetic irrational divisions of octave |
| | * AIDINO = Arithmetic irrational divisions of irrational non-octave |
| | * AIDRNO = Arithmetic irrational divisions of rational non-octave |
| | * AIDRI = Arithmetic irrational divisions of rational interval |
| | * AIDII = Arithmetic irrational divisions of irrational interval |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;"> If A1=175.0 then we have 8-AID(1400.)</span>
| | Example: [http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 Baran scale] |
|
| |
|
| <span style="font-family: Tahoma,Geneva,sans-serif;"> If A1=56 then we have 700-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> 28 73 135 214 310 423 553 700</span></span>
| | [[Category:AID]] |
| | |
| <span style="font-family: Tahoma,Geneva,sans-serif;"> <span style="color: black; font-size: 10pt;">If A1=87.5 then we have 112-AID(1400.) with Degrees as <span style="color: black; font-size: 10pt;"> 7 16 27 40 55 72 91 112</span></span></span>
| |
| | |
| <span style="font-family: Tahoma,Geneva,sans-serif;"><u>AID</u> sytem shows different ascending , descending or linear trend of change in divisions sizes due to relation between n and A1 in <u>AID</u><span style="color: black; font-size: 10pt;"> and <u>EDO</u> with equal degree:</span></span>
| |
| | |
| <ul><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> greater than division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is negative and </span><u><span style="color: black; font-size: 10pt;">AID</span></u><span style="color: black; font-size: 10pt;"> is descending.</span></span></li><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> smaller than division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is positive and </span><u><span style="color: black; font-size: 10pt;">AID</span></u><span style="color: black; font-size: 10pt;"> is ascending.</span></span></li><li><span style="font-family: Tahoma,Geneva,sans-serif;">If choosing <u><span style="color: black; font-size: 10pt;">A1</span></u><span style="color: black; font-size: 10pt;"> equal to division size in equal degree </span><u><span style="color: black; font-size: 10pt;">EDO</span></u><span style="color: black; font-size: 10pt;"> , </span><u><span style="color: black; font-size: 10pt;">d</span></u><span style="color: black; font-size: 10pt;"> is zero.</span>**</span></li></ul>
| |
| | |
| <div class='external-image-warning' style='background-color:#f8f9fa; border: 1px solid #eaecf0; padding-left: 0.5em; padding-right:0.5em; display:inline-block'>
| |
| External image: http://sites.google.com/site/240edo/AIDO-custom-size-298-402.jpg<br>
| |
| : <small><b>WARNING</b>: MediaWiki doesn't have very good support for external images.</small><br>
| |
| : <small>Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.</small>
| |
| </div>
| |
| [[Category:IMPORTDEBUG - Change External Images]]
| |
| | |
| ==<span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 13.3333px;">171.4285714 is point of intersection in these 3 trends:</span>==
| |
| | |
| <div class='external-image-warning' style='background-color:#f8f9fa; border: 1px solid #eaecf0; padding-left: 0.5em; padding-right:0.5em; display:inline-block'>
| |
| External image: http://sites.google.com/site/240edo/AIDO2.jpg<br>
| |
| : <small><b>WARNING</b>: MediaWiki doesn't have very good support for external images.</small><br>
| |
| : <small>Furthermore, since external images can break, we recommend that you replace the above with a local copy of the image.</small>
| |
| </div>
| |
| [[Category:IMPORTDEBUG - Change External Images]]
| |
| | |
| we can have different kinds of AID:
| |
| | |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDO = Arithmetic irrational divisions of octave</span></u></span>
| |
| | |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDINO = Arithmetic irrational divisions of irrational non-octave</span></u></span>
| |
| | |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDRNO = Arithmetic irrational divisions of rational non-octave</span></u></span>
| |
| | |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDRI = Arithmetic irrational divisions of rational interval</span></u></span>
| |
| | |
| <span style="display: block; font-family: Tahoma,Geneva,sans-serif; font-size: 14px; text-align: left;"><u><span style="color: #000000; font-family: arial,sans-serif;">AIDII = Arithmetic irrational divisions of irrational interval</span></u></span>
| |
| | |
| <span style="color: #000000; font-family: Tahoma,Geneva,sans-serif; font-size: 12px; text-decoration: none;">[http://sites.google.com/site/240edo/arithmeticirrationaldivisions%28aid%29 **Example : Baran scale**]</span> [[Category:AID]]
| |
| [[Category:Shaahin_Mohajeri]] | | [[Category:Shaahin_Mohajeri]] |
| [[Category:todo:cleanup]] | | [[Category:todo:cleanup]] |
Arithmetic irrational divisions
For an intervallic system with n divisions, AID is considered as arithmetic sequence with divisions of system as terms of sequence.
If the first division is A1 and the last , An , with common difference of d , we have :
- A1 = A1
- A2 = A1+d
- A3 = A1+2d
- A4 = A1+3d
- ...
- An = A1+(n-1)d
So sum of the divisions is Sn :
- Sn =( n[2A1+(n-1)d])/2
As we can consider Sn of system to be 1200 cent or anything else (octavic or non-octavic system ) then d is most important to make an AID with n divisions with A1. So, the common difference between divisions is :
- d =( 2(Sn - nA1))/((n(n-1))
By considering Sn=1200 , A1=70 , n=12 , d will be 5.454545455 and our 12-tone scale is equal to:
- 0.0 70.0 145.455 226.364 312.727 404.545 501.818 604.545 712.727 826.364 945.455 1070.0 1200.0
Scales based on AID can be subsets of EDO if:
- we choose d=0 so , A1 = Sn/n .. Consider n=8 and A1=150 , then we have 8-EDO .
- for a constant n and different A1, if d and (Sn/A1) are integers, we have a subset of EDO or EDI (Equal divisions of Interval).
Consider Sn = 1400 , n=8 and A1=70 , then we have a subset of a 140-ED (1400.) with Degrees as 7 17 30 46 65 87 112 140 :
- 0.0 70.0 170.0 300.0 460.0 650.0 870.0 1120.0 1400.0
And now for Sn=1400 and n=8,
- If A1=175.0 then we have 8-AID(1400.)
- If A1=56 then we have 700-AID(1400.) with Degrees as 28 73 135 214 310 423 553 700
- If A1=87.5 then we have 112-AID(1400.) with Degrees as 7 16 27 40 55 72 91 112
AID system shows different ascending, descending or linear trend of change in divisions sizes due to relation between n and A1 in AID and EDO with equal degree:
- If choosing A1 greater than division size in equal degree EDO , d is negative and AID is descending.
- If choosing A1 smaller than division size in equal degree EDO , d is positive and AID is ascending.
- If choosing A1 equal to division size in equal degree EDO , d is zero.
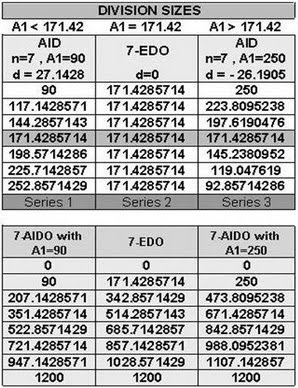
171.4285714 is point of intersection in these 3 trends:
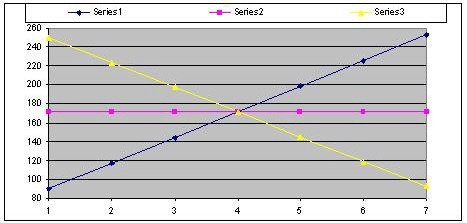
We can have different kinds of AID:
- AIDO = Arithmetic irrational divisions of octave
- AIDINO = Arithmetic irrational divisions of irrational non-octave
- AIDRNO = Arithmetic irrational divisions of rational non-octave
- AIDRI = Arithmetic irrational divisions of rational interval
- AIDII = Arithmetic irrational divisions of irrational interval
Example: Baran scale

