Kite's thoughts on the mathematical basis For the kite guitar
Consider this sequence: 9/8 -- 7/6 -- 6/5 -- 5/4 -- 9/7 -- 4/3. These are sequential intervals on one string of the Kite Guitar, and this is the essence of what makes it so playable. 1/1 must of course be on the next string down, to make each of these ratios available to play as an interval. Since 6/5 and 5/4 add up to 3/2, we know that 3/2 is on the next string up. And 3/2 plus 4/3 is 2/1, thus 2/1 is on the next string up after 3/2. From this we can derive the entire layout. The next chart shows the downmajor tuning, but this analysis also applies to the upminor and upmajor tunings. Alternate tunings merely shift the ratios on each string sideways.
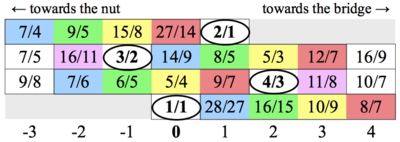
What if this sequence from 9/8 to 4/3 was all we knew of the guitar? Could we deduce that it is in 41-edo? No, but we can work backwards from the notes to deduce what commas are being tempered out. From 9/8 to 6/5 = 16/15 = 2 frets. From 6/5 to 5/4 = 25/24 = 1 fret. Thus (25/24)^2 = 16/15, which gives us the Laquinyo or Magic comma 3125/3072 = [-10 -1 5]. This comma is the difference between (5/4)^5 and 3/1, thus its pergen is #37, (P8, P12/5).
This temperament can be extended to prime limit 7 and 11. 9/8 to 7/6 = 28/27 = 1 fret. 6/5 to 5/4 = 25/24 = 1 fret. Thus 28/27 = 25/24, which gives us the Ruyoyo comma 225/224. Extending the sequence of ratios, we get 9/8 -- 7/6 -- 6/5 -- 5/4 -- 9/7 -- 4/3 -- 11/8. From 4/3 to 11/8 = 33/32 = 1 fret. Since 25/25 is also 1 fret, 33/32 = 25/24, which implies the Luyoyo comma 100/99. Tempering out Laquinyo and Ruyoyo and Luyoyo gives us 11-limit Laquinyo/Magic. These are both strong extensions, i.e. the pergen doesn't change.
This pergen is easily notated with a single additional pair of accidentals. From the pergen notation guide, which assumes that the octave is untempered, and the fifth is tuned to 700 + c cents, where c is a free variable:
Period = P8 = 1200¢, Generator = vM3 = ^4dd4 = 380¢ + c/5, Enharmonic = ^5dd2 = 0¢, ^5C = B##, and ^ = 20¢ + 3.8c
This table, also from the pergen notation guide, shows a 20-step section of the pergen's genchain. The first row shows the cents of each interval from the tonic, the second shows the interval name, and the third shows the note names in the key of D, using ups and downs notation.
| 1000¢ -2c |
180¢ -1.8c |
560¢ -1.6c |
940¢ -1.4c |
120¢ -1.2c |
500¢ -c |
880¢ -0.8c |
60¢ -0.6c |
440¢ -0.4c |
820¢ -0.2c |
0¢ | 380¢ +0.2c |
760¢ +0.4c |
1140¢ +0.6c |
320¢ +0.8c |
700¢ +c |
1080 +1.2c |
260¢ +1.4c |
640¢ +1.6c |
1020 +1.8c |
200¢ +2c |
| m7 | vM2 | vvA4 | ^^d7 | ^m2 | P4 | vM6 | vvA1 | ^^d4 | ^m6 | P1 | vM3 | vvA5 | ^^d8 | ^m3 | P5 | vM7 | vvA2 | ^^d5 | ^m7 | M2 |
| C | vE | vvG# | ^^Cb | ^Eb | G | vB | vvD# | ^^Gb | ^Bb | D | vF# | vvA# | ^^Db | ^F | A | vC# | vvE# | ^^Ab | ^C | E |
Extrapolating fourthwards, 32/27 is 300¢ - 3c. This interval occurs from 9/8 to 4/3, which is 5 frets. Thus one fret is 1/5 of 32/27,which comes to 60¢ - 0.6c. Assuming a downmajor tuning, the adjacent-open-string-interval is the generator, 380¢ + 0.2c. The fretboard looks like this:
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| P8+520+2.8c | P8+580+2.2c | P8+640+1.6c | P8+700+c | P8+760+0.4c | P8+820-0.2c | P8+880-0.8c | P8+940-1.4c |
| P8+140+2.6c | P8+200+2c | P8+260+1.4c | P8+320+0.8c | P8+380+0.2c | P8+440-0.4c | P8+500-c | P8+560-1.6c |
| 960+2.4c | 1020+1.8c | 1080+1.2c | 1140+0.6c | 1200¢ (P8) | P8+60-0.6c | P8+120-1.2c | P8+180-1.8c |
| 580+2.2c | 640+1.6c | 700+c | 760+0.4c | 820-0.2c | 880-0.8c | 940-1.4c | 1000-2c |
| 200+2c | 260+1.4c | 320+0.8c | 380+0.2c | 440-0.4c | 500-c | 560-1.6c | 620-2.2c |
| 1020+1.8c-P8 | 1080+1.2c-P8 | 1140+0.6c-P8 | 0¢ | 60-0.6c | 120-1.2c | 180-1.8c | 240-2.4c |
Certain values of c result in edos. For example, c = 2.44¢ gives us 41-edo. Most values of c do not result in edos. Can the accuracy of the tuning be improved over 41-edo by freely varying c? Increasing c brings 5/4 more in tune, but quickly throws 3/2 out of tune. The optimal tuning of this temperament is very close to 41-edo, and as we'll see below, non-edo tunings are very impractical.
Which edos support the Kite tuning? The edo must support the pergen (P8, P12/5). The simplest edo in which the 12th can be divided into 5 equal parts is the one in which the 12th actually equals 5 edosteps. This is 3-edo, which is much too inaccurate to be musically useful. However the set of all edos that support this pergen appear in the scale tree on the spine of the 2\3 kite, and on every 5th ripple line from the kite. (See the notation guide for edos 5-72 for an explanation of kites, spines and ripple lines.) These edos support the pergen, but may or may not temper out the required commas Laquinzo, Ruyoyo and Luyoyo. Those that do temper out these commas are:
- 1st ripple line: 19-edo, 22-edo
- 2nd ripple line: 41-edo, (44-edo)
- 3rd ripple line: 60-edo, 63-edo
- 4th ripple line: (82-edo), 85-edo
- 5th ripple line: 104-edo
The edos on the 1st line needn't omit any frets, those on the 2nd line must omit every other fret, those on the 3rd line must omit 2 out of every 3 frets, etc. Note that every other fret of 44-edo is identical to 22-edo, and every 4th fret of 82-edo is identical to every other fret of 41-edo. Thus 19edo and 22edo guitars can mimic Kite guitars if the open strings are tuned in 3rds. For 19-edo, c = -5.26¢, and for 22-edo, c = 9.09¢.
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| 505¢+P8 | 568¢+P8 | 632¢+P8 | 695¢+P8 | 758¢+P8 | 821¢+P8 | 884¢+P8 | 947¢+P8 |
| 126¢+P8 | 189¢+P8 | 253¢+P8 | 316¢+P8 | 379¢+P8 | 442¢+P8 | 505¢+P8 | 568¢+P8 |
| 947¢ | 1012¢ | 1074¢ | 1137¢ | 1200¢ (P8) | 63¢+P8 | 126¢+P8 | 189¢+P8 |
| 568¢ | 632¢ | 695¢ | 758¢ | 821¢ | 884¢ | 947¢ | 1012¢ |
| 189¢ | 253¢ | 316¢ | 379¢ | 442¢ | 505¢ | 568¢ | 632¢ |
| 1012¢-P8 | 1074¢-P8 | 1137¢-P8 | 0¢ | 63¢ | 126¢ | 189¢ | 253¢ |
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|
| 545¢+P8 | 600¢+P8 | 655¢+P8 | 709¢+P8 | 764¢+P8 | 818¢+P8 | 873¢+P8 | 927¢+P8 |
| 164¢+P8 | 218¢+P8 | 273¢+P8 | 327¢+P8 | 381¢+P8 | 436¢+P8 | 491¢+P8 | 545¢+P8 |
| 981¢ | 1036¢ | 1091¢ | 1145¢ | 1200¢ (P8) | 55¢+P8 | 109¢+P8 | 164¢+P8 |
| 600¢ | 655¢ | 709¢ | 764¢ | 818¢ | 873¢ | 927¢ | 981¢ |
| 218¢ | 273¢ | 327¢ | 381¢ | 436¢ | 491¢ | 545¢ | 600¢ |
| 1036¢-P8 | 1091¢-P8 | 1145¢-P8 | 0¢ | 55¢ | 109¢ | 164¢ | 218¢ |
For 19, 22, 41, 60, etc., the ratios within the immediate area of 1/1 are all the same, except for how well tuned they are. But the ratios up the neck are quite different. With 41, 12 frets up 1 string make 3/2. But in 19, 3/2 is 11 frets. In 22, it's 13 frets. In 41, the octave is up 1 string and up 14 frets, which I write as (+1,+14). In 19, its (+1,+13), and in 22, it's (+1, +15). But in a non-edo tuning of Laquinyo/Magic, the 8ve doesn't appear anywhere up the neck.
This is a huge disadvantage to a non-edo Kite guitar, because when two guitarists play together, with a 41-edo tuning, one guitarist can solo 14 frets above the other.