User:Nick Vuci/TonalityDiamond: Difference between revisions
consolidated diagram and construction section |
|||
| Line 9: | Line 9: | ||
File:How to tonality diamond 1.png|'''Step 1: Take the numbers of an odd-limit and arrange them along two axes.''' | File:How to tonality diamond 1.png|'''Step 1: Take the numbers of an odd-limit and arrange them along two axes.''' | ||
File:How to tonality diamond 2.png|'''Step 2: Using one row as the numerator and the other as the denominator, fill in the cells with the ratios they form.''' | File:How to tonality diamond 2.png|'''Step 2: Using one row as the numerator and the other as the denominator, fill in the cells with the ratios they form.''' | ||
File:How to tonality diamond 3.png|'''Step 3: Make sure the decimal form of the | File:How to tonality diamond 3.png|'''Step 3: Make sure the decimal form of the ratios is between 1 and 2. If it is not, double one of the numbers until it is.''' | ||
File:How to tonality diamond 4.png|'''Optional step: to make the rows play rooted chords, one half of the diamond (not including the middle unison row) must be lowered by an octave (represented by grey cells in image).''' | File:How to tonality diamond 4.png|'''Optional step: to make the rows play rooted chords, one half of the diamond (not including the middle unison row) must be lowered by an octave (represented by grey cells in image).''' | ||
</gallery>Note: the numbers of the odd-limit are generally arranged in one of three ways: a) ascending numerically (ie, 2 3 5 7 9 11 etc) or, b) ascending by tonal order (ie 2 9 5 11 3 7), or c) ascending chordally (ie, 2 5 3 7 9 11). | </gallery>Note: the numbers of the odd-limit are generally arranged in one of three ways: a) ascending numerically (ie, 2 3 5 7 9 11 etc) or, b) ascending by tonal order (ie 2 9 5 11 3 7), or c) ascending chordally (ie, 2 5 3 7 9 11). | ||
Revision as of 06:00, 10 May 2025
WORK-IN-PROGRESS AS OF 07MAY2025
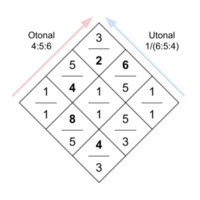
The tonality diamond is a symmetric organization of otonal and utonal chords based around a central note and bounded by an odd-limit. First formalized in the 7-odd-limit by Max F Meyer in 1929, they became central to the music and theories of Harry Partch, who built his tonal system around the 11-odd-limit tonality diamond. The principle has been used both conceptually (such as for target intervals of temperaments) and practically (such as for instrument layouts) in xenharmonics ever since.
Play some tonality diamonds to hear how they sound.
Construction
-
Step 1: Take the numbers of an odd-limit and arrange them along two axes.
-
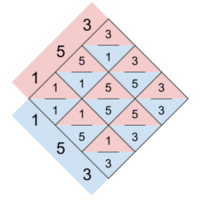
Step 2: Using one row as the numerator and the other as the denominator, fill in the cells with the ratios they form.
-
Step 3: Make sure the decimal form of the ratios is between 1 and 2. If it is not, double one of the numbers until it is.
-
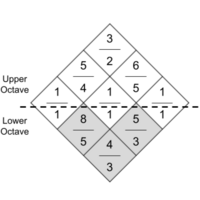
Optional step: to make the rows play rooted chords, one half of the diamond (not including the middle unison row) must be lowered by an octave (represented by grey cells in image).
Note: the numbers of the odd-limit are generally arranged in one of three ways: a) ascending numerically (ie, 2 3 5 7 9 11 etc) or, b) ascending by tonal order (ie 2 9 5 11 3 7), or c) ascending chordally (ie, 2 5 3 7 9 11).
History
The tonality diamond was first formally explained by Max F. Meyer in his 1929 publication The Musician's Arithmetic[1] using the 7-odd-limit. Even though Harry Partch gives a different story for how he discovered the concept, it is likely this source that gave him the idea, which he then extended to the 11-odd-limit and made the basis of his tonal system.
Erv Wilson in particular was inspired by the tonality diamond and developed a number of "diamonds" himself.[2]
The first novel xenharmonic temperament — George Secor's later-named "Miracle" temperament — was made to approximate Partch's 11-limit diamond.
Uses
Instrument layout
The most famous example of the tonality diamond as a practical layout for an instrument is Harry Partch's "Diamond Marimba," which uses the 11-odd-limit tonality diamond exactly. This idea was explored further with Partch's "Quadrangularis Reversum," and by Cris Forster with his 13-odd-limit "Diamond Marimba."
Play with Partch’s Diamond Marimba here.