User:BudjarnLambeth/Sandbox2: Difference between revisions

From Xenharmonic Wiki
Jump to navigation Jump to search
← Older editNewer edit →
VisualWikitext
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,543 edits
BudjarnLambeth (talk | contribs)
autopatrolled, emailconfirmed
18,543 edits
Line 8: Line 8:


; 32edo
; 32edo
* Step size: 37.500{{c}}, octave size: 1200.00{{c}}  
* Step size: 37.500{{c}}, octave size: 1200.0{{c}}  
Pure-octaves 32edo approximates all harmonics up to 16 within NNN{{c}}.
Pure-octaves 32edo approximates all harmonics up to 16 within NNN{{c}}.
{{Harmonics in equal|32|2|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32edo}}
{{Harmonics in equal|32|2|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32edo}}
Line 14: Line 14:


; [[WE|32et, 13-limit WE tuning]]  
; [[WE|32et, 13-limit WE tuning]]  
* Step size: 37.481{{c}}, octave size: NNN{{c}}
* Step size: 37.481{{c}}, octave size: 1199.4{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. Its 13-limit WE tuning and 13-linut [[TE]] tuning both do this.
Compressing the octave of 32edo by around half a cent results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. Its 13-limit WE tuning and 13-linut [[TE]] tuning both do this.
{{Harmonics in cet|37.481|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 13-limit WE tuning}}
{{Harmonics in cet|37.481|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 13-limit WE tuning}}
{{Harmonics in cet|37.481|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in ETNAME, SUBGROUP WE tuning (continued)}}
{{Harmonics in cet|37.481|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in ETNAME, SUBGROUP WE tuning (continued)}}


; [[WE|32et, 11-limit WE tuning]]  
; [[WE|32et, 11-limit WE tuning]]  
* Step size: 37.453{{c}}, octave size: NNN{{c}}
* Step size: 37.453{{c}}, octave size: 1198.5{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. Its 11-limit WE tuning and 11-limit [[TE]] tuning both do this.
Compressing the octave of 32edo by around 1.5{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. Its 11-limit WE tuning and 11-limit [[TE]] tuning both do this.
{{Harmonics in cet|37.453|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning}}
{{Harmonics in cet|37.453|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning}}
{{Harmonics in cet|37.453|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning (continued)}}
{{Harmonics in cet|37.453|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 32et, 11-limit WE tuning (continued)}}


; [[90ed7]]  
; [[90ed7]]  
* Step size: NNN{{c}}, octave size: NNN{{c}}
* Step size: 37.431{{c}}, octave size: 1197.8{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. If one wishes to use both of 32edo's mappings of the 5th harmonic simultaneously, this tuning is suited to that due to evenly sharing the error between them. The tuning 90ed7 does this.
Compressing the octave of 32edo by around 2{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. If one wishes to use both of 32edo's mappings of the 5th harmonic simultaneously, this tuning is suited to that due to evenly sharing the error between them. The tuning 90ed7 does this.
{{Harmonics in equal|90|7|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 90ed7}}
{{Harmonics in equal|90|7|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 90ed7}}
{{Harmonics in equal|90|7|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 90ed7 (continued)}}
{{Harmonics in equal|90|7|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 90ed7 (continued)}}
Line 34: Line 34:
* Step size: 37.418{{c}}, octave size: 1197.375{{c}}
* Step size: 37.418{{c}}, octave size: 1197.375{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 133zpi does this.
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 133zpi does this.
{{Harmonics in cet|100|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 133zpi}}
{{Harmonics in cet|37.418|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 133zpi}}
{{Harmonics in cet|100|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 133zpi (continued)}}
{{Harmonics in cet|37.418|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 133zpi (continued)}}
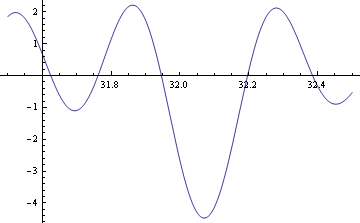
Below is a plot of the [[Zeta]] function, showing how its peak (ie biggest absolute value) is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.
Below is a plot of the [[Zeta]] function, showing how its peak (ie biggest absolute value) is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.


Line 41: Line 41:


; [[51edt]]  
; [[51edt]]  
* Step size: NNN{{c}}, octave size: NNN{{c}}
* Step size: 37.293{{c}}, octave size: 1193.4{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 51edt does this.
Compressing the octave of 32edo by around 6.5{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 51edt does this.
{{Harmonics in equal|51|3|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 51edt}}
{{Harmonics in equal|51|3|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 51edt}}
{{Harmonics in equal|51|3|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 51edt (continued)}}
{{Harmonics in equal|51|3|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 51edt (continued)}}


; [[zpi|134zpi]]  
; [[zpi|134zpi]]  
* Step size: 37.176{{c}}, octave size: NNN{{c}}
* Step size: 37.176{{c}}, octave size: 1189.6{{c}}
Compressing the octave of 134zpi by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 134zpi does this.
Compressing the octave of 134zpi by around 10.5{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 134zpi does this.
{{Harmonics in cet|37.176|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 134zpi}}
{{Harmonics in cet|37.176|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 134zpi}}
{{Harmonics in cet|37.176|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 134zpi (continued)}}
{{Harmonics in cet|37.176|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 134zpi (continued)}}


; [[75ed5]]  
; [[75ed5]]  
* Step size: NNN{{c}}, octave size: NNN{{c}}
* Step size: 37.151{{c}}, octave size: 1188.8{{c}}
Compressing the octave of 32edo by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 75ed5 does this.
Compressing the octave of 32edo by around 11{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning 75ed5 does this.
{{Harmonics in equal|75|5|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 75ed5}}
{{Harmonics in equal|75|5|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in 75ed5}}
{{Harmonics in equal|75|5|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 75ed5 (continued)}}
{{Harmonics in equal|75|5|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in 75ed5 (continued)}}
; [[WE|ETNAME, SUBGROUP WE tuning]]
* Step size: NNN{{c}}, octave size: NNN{{c}}
_ing the octave of EDONAME by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. Its SUBGROUP WE tuning and SUBGROUP [[TE]] tuning both do this.
{{Harmonics in cet|100|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in ETNAME, SUBGROUP WE tuning}}
{{Harmonics in cet|100|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in ETNAME, SUBGROUP WE tuning (continued)}}
; [[EDONOI]]
* Step size: NNN{{c}}, octave size: NNN{{c}}
_ing the octave of EDONAME by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning EDONOI does this.
{{Harmonics in equal|12|2|1|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in EDONOI}}
{{Harmonics in equal|12|2|1|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in EDONOI (continued)}}
; [[zpi|ZPINAME]]
* Step size: NNN{{c}}, octave size: NNN{{c}}
_ing the octave of EDONAME by around NNN{{c}} results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN{{c}}. The tuning ZPINAME does this.
{{Harmonics in cet|100|intervals=integer|columns=11|collapsed=true|title=Approximation of harmonics in ZPINAME}}
{{Harmonics in cet|100|intervals=integer|columns=12|start=12|collapsed=true|title=Approximation of harmonics in ZPINAME (continued)}}


= Title2 =
= Title2 =

Revision as of 23:30, 29 August 2025

Quick link

User:BudjarnLambeth/Draft related tunings section

Title1

Octave stretch or compression

What follows is a comparison of compressed-octave 32edo tunings.

32edo
  • Step size: 37.500 ¢, octave size: 1200.0 ¢

Pure-octaves 32edo approximates all harmonics up to 16 within NNN ¢.

Approximation of harmonics in 32edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +0.0 +10.5 +0.0 -11.3 +10.5 +6.2 +0.0 -16.4 -11.3 +11.2 +10.5
Relative (%) +0.0 +28.1 +0.0 -30.2 +28.1 +16.5 +0.0 -43.8 -30.2 +29.8 +28.1
Steps
(reduced) 		32
(0) 		51
(19) 		64
(0) 		74
(10) 		83
(19) 		90
(26) 		96
(0) 		101
(5) 		106
(10) 		111
(15) 		115
(19)
Approximation of harmonics in 32edo (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -15.5 +6.2 -0.8 +0.0 +7.5 -16.4 +2.5 -11.3 +16.7 +11.2 +9.2 +10.5
Relative (%) -41.4 +16.5 -2.0 +0.0 +20.1 -43.8 +6.6 -30.2 +44.6 +29.8 +24.6 +28.1
Steps
(reduced) 		118
(22) 		122
(26) 		125
(29) 		128
(0) 		131
(3) 		133
(5) 		136
(8) 		138
(10) 		141
(13) 		143
(15) 		145
(17) 		147
(19)
32et, 13-limit WE tuning
  • Step size: 37.481 ¢, octave size: 1199.4 ¢

Compressing the octave of 32edo by around half a cent results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. Its 13-limit WE tuning and 13-linut TE tuning both do this.

Approximation of harmonics in 32et, 13-limit WE tuning
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -0.6 +9.6 -1.2 -12.7 +9.0 +4.5 -1.8 -18.3 -13.3 +9.1 +8.4
Relative (%) -1.6 +25.5 -3.2 -33.9 +23.9 +11.9 -4.9 -48.9 -35.6 +24.2 +22.3
Step 32 51 64 74 83 90 96 101 106 111 115
Approximation of harmonics in ETNAME, SUBGROUP WE tuning (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -17.8 +3.9 -3.1 -2.4 +5.1 +18.5 -0.1 -13.9 +14.0 +8.5 +6.5 +7.8
Relative (%) -47.4 +10.3 -8.4 -6.5 +13.5 +49.5 -0.3 -37.2 +37.5 +22.6 +17.3 +20.7
Step 118 122 125 128 131 134 136 138 141 143 145 147
32et, 11-limit WE tuning
  • Step size: 37.453 ¢, octave size: 1198.5 ¢

Compressing the octave of 32edo by around 1.5 ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. Its 11-limit WE tuning and 11-limit TE tuning both do this.

Approximation of harmonics in 32et, 11-limit WE tuning
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -1.5 +8.1 -3.0 -14.8 +6.6 +1.9 -4.5 +16.3 -16.3 +6.0 +5.1
Relative (%) -4.0 +21.8 -8.0 -39.5 +17.7 +5.2 -12.0 +43.5 -43.5 +15.9 +13.7
Step 32 51 64 74 83 90 96 102 106 111 115
Approximation of harmonics in 32et, 11-limit WE tuning (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +16.4 +0.4 -6.6 -6.0 +1.4 +14.8 -3.9 -17.8 +10.1 +4.5 +2.4 +3.6
Relative (%) +43.7 +1.2 -17.7 -16.1 +3.7 +39.5 -10.4 -47.5 +26.9 +11.9 +6.4 +9.7
Step 119 122 125 128 131 134 136 138 141 143 145 147
90ed7
  • Step size: 37.431 ¢, octave size: 1197.8 ¢

Compressing the octave of 32edo by around 2 ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. If one wishes to use both of 32edo's mappings of the 5th harmonic simultaneously, this tuning is suited to that due to evenly sharing the error between them. The tuning 90ed7 does this.

Approximation of harmonics in 90ed7
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -2.2 +7.0 -4.4 -16.4 +4.9 +0.0 -6.6 +14.1 -18.6 +3.6 +2.7
Relative (%) -5.9 +18.8 -11.7 -43.8 +13.0 +0.0 -17.6 +37.6 -49.7 +9.5 +7.1
Steps
(reduced) 		32
(32) 		51
(51) 		64
(64) 		74
(74) 		83
(83) 		90
(0) 		96
(6) 		102
(12) 		106
(16) 		111
(21) 		115
(25)
Approximation of harmonics in 90ed7 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +13.8 -2.2 -9.3 -8.8 -1.4 +11.9 -6.8 +16.7 +7.0 +1.4 -0.7 +0.5
Relative (%) +36.9 -5.9 -25.0 -23.5 -3.9 +31.8 -18.3 +44.5 +18.8 +3.7 -1.9 +1.2
Steps
(reduced) 		119
(29) 		122
(32) 		125
(35) 		128
(38) 		131
(41) 		134
(44) 		136
(46) 		139
(49) 		141
(51) 		143
(53) 		145
(55) 		147
(57)
133zpi
  • Step size: 37.418 ¢, octave size: 1197.375 ¢

Compressing the octave of 32edo by around NNN ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning 133zpi does this.

Approximation of harmonics in 133zpi
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -2.6 +6.4 -5.2 -17.4 +3.7 -1.2 -7.9 +12.7 +17.4 +2.1 +1.1
Relative (%) -7.0 +17.0 -14.0 -46.5 +10.0 -3.2 -21.0 +34.0 +46.5 +5.6 +3.0
Step 32 51 64 74 83 90 96 102 107 111 115
Approximation of harmonics in 133zpi (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +12.2 -3.8 -11.0 -10.5 -3.2 +10.1 -8.7 +14.8 +5.2 -0.5 -2.7 -1.5
Relative (%) +32.6 -10.2 -29.4 -28.1 -8.5 +27.0 -23.2 +39.5 +13.8 -1.5 -7.1 -4.0
Step 119 122 125 128 131 134 136 139 141 143 145 147

Below is a plot of the Zeta function, showing how its peak (ie biggest absolute value) is shifted above 32, corresponding to a zeta tuning with octaves flattened to 1197.375 cents. This will improve the fifth, at the expense of the third.

plot32.png

51edt
  • Step size: 37.293 ¢, octave size: 1193.4 ¢

Compressing the octave of 32edo by around 6.5 ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning 51edt does this.

Approximation of harmonics in 51edt
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -6.6 +0.0 -13.2 +10.7 -6.6 -12.4 +17.4 +0.0 +4.1 -11.8 -13.2
Relative (%) -17.7 +0.0 -35.5 +28.6 -17.7 -33.3 +46.8 +0.0 +10.9 -31.6 -35.5
Steps
(reduced) 		32
(32) 		51
(0) 		64
(13) 		75
(24) 		83
(32) 		90
(39) 		97
(46) 		102
(0) 		107
(5) 		111
(9) 		115
(13)
Approximation of harmonics in 51edt (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -2.6 +18.2 +10.7 +10.8 +17.8 -6.6 +11.7 -2.6 -12.4 -18.4 +16.5 +17.4
Relative (%) -7.1 +48.9 +28.6 +29.0 +47.6 -17.7 +31.3 -6.8 -33.3 -49.3 +44.3 +46.8
Steps
(reduced) 		119
(17) 		123
(21) 		126
(24) 		129
(27) 		132
(30) 		134
(32) 		137
(35) 		139
(37) 		141
(39) 		143
(41) 		146
(44) 		148
(46)
134zpi
  • Step size: 37.176 ¢, octave size: 1189.6 ¢

Compressing the octave of 134zpi by around 10.5 ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning 134zpi does this.

Approximation of harmonics in 134zpi
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -10.4 -6.0 +16.4 +1.9 -16.3 +14.2 +6.1 -12.0 -8.5 +12.4 +10.5
Relative (%) -27.9 -16.1 +44.2 +5.1 -44.0 +38.2 +16.3 -32.2 -22.8 +33.3 +28.1
Step 32 51 65 75 83 91 97 102 107 112 116
Approximation of harmonics in 134zpi (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -16.6 +3.8 -4.1 -4.3 +2.3 +14.8 -4.4 +18.3 +8.2 +2.0 -0.6 +0.1
Relative (%) -44.6 +10.3 -11.0 -11.6 +6.1 +39.9 -11.8 +49.3 +22.1 +5.4 -1.6 +0.3
Step 119 123 126 129 132 135 137 140 142 144 146 148
75ed5
  • Step size: 37.151 ¢, octave size: 1188.8 ¢

Compressing the octave of 32edo by around 11 ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning 75ed5 does this.

Approximation of harmonics in 75ed5
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) -11.2 -7.3 +14.8 +0.0 -18.4 +11.9 +3.6 -14.5 -11.2 +9.6 +7.5
Relative (%) -30.1 -19.5 +39.9 +0.0 -49.6 +32.0 +9.8 -39.1 -30.1 +25.8 +20.3
Steps
(reduced) 		32
(32) 		51
(51) 		65
(65) 		75
(0) 		83
(8) 		91
(16) 		97
(22) 		102
(27) 		107
(32) 		112
(37) 		116
(41)
Approximation of harmonics in 75ed5 (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) +17.6 +0.7 -7.3 -7.5 -1.0 +11.5 -7.8 +14.8 +4.6 -1.6 -4.3 -3.6
Relative (%) +47.3 +2.0 -19.5 -20.3 -2.8 +30.8 -21.1 +39.9 +12.5 -4.3 -11.4 -9.8
Steps
(reduced) 		120
(45) 		123
(48) 		126
(51) 		129
(54) 		132
(57) 		135
(60) 		137
(62) 		140
(65) 		142
(67) 		144
(69) 		146
(71) 		148
(73)










ETNAME, SUBGROUP WE tuning
  • Step size: NNN ¢, octave size: NNN ¢

_ing the octave of EDONAME by around NNN ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. Its SUBGROUP WE tuning and SUBGROUP TE tuning both do this.

Approximation of harmonics in ETNAME, SUBGROUP WE tuning
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Relative (%) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Step 12 19 24 28 31 34 36 38 40 42 43
Approximation of harmonics in ETNAME, SUBGROUP WE tuning (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Relative (%) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Step 44 46 47 48 49 50 51 52 53 54 54 55
EDONOI
  • Step size: NNN ¢, octave size: NNN ¢

_ing the octave of EDONAME by around NNN ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning EDONOI does this.

Approximation of harmonics in EDONOI
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Relative (%) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Steps
(reduced) 		12
(0) 		19
(7) 		24
(0) 		28
(4) 		31
(7) 		34
(10) 		36
(0) 		38
(2) 		40
(4) 		42
(6) 		43
(7)
Approximation of harmonics in EDONOI (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Relative (%) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Steps
(reduced) 		44
(8) 		46
(10) 		47
(11) 		48
(0) 		49
(1) 		50
(2) 		51
(3) 		52
(4) 		53
(5) 		54
(6) 		54
(6) 		55
(7)
ZPINAME
  • Step size: NNN ¢, octave size: NNN ¢

_ing the octave of EDONAME by around NNN ¢ results in improved primes NNN, but worse primes NNN. This approximates all harmonics up to 16 within NNN ¢. The tuning ZPINAME does this.

Approximation of harmonics in ZPINAME
Harmonic 2 3 4 5 6 7 8 9 10 11 12
Error Absolute (¢) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Relative (%) +0.0 -2.0 +0.0 +13.7 -2.0 +31.2 +0.0 -3.9 +13.7 +48.7 -2.0
Step 12 19 24 28 31 34 36 38 40 42 43
Approximation of harmonics in ZPINAME (continued)
Harmonic 13 14 15 16 17 18 19 20 21 22 23 24
Error Absolute (¢) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Relative (%) -40.5 +31.2 +11.7 +0.0 -5.0 -3.9 +2.5 +13.7 +29.2 +48.7 -28.3 -2.0
Step 44 46 47 48 49 50 51 52 53 54 54 55

Title2

Lab

Place holder








Approximation of prime harmonics in 1ed300c
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) +0 -102 -86 -69 +49 +59 -105 +2 -28 -130 +55
Relative (%) +0.0 -34.0 -28.8 -22.9 +16.2 +19.8 -35.0 +0.8 -9.4 -43.2 +18.3
Step 4 6 9 11 14 15 16 17 18 19 20


Approximation of prime harmonics in 140ed12
Harmonic 2 3 5 7 11 13 17 19 23 29 31
Error Absolute (¢) -1.6 +3.2 +10.0 +11.3 -3.0 +15.1 +11.6 +3.4 +10.6 +8.8 -14.5
Relative (%) -5.2 +10.4 +32.4 +36.7 -9.8 +49.0 +37.6 +11.0 +34.6 +28.6 -47.1
Steps
(reduced) 		39
(39) 		62
(62) 		91
(91) 		110
(110) 		135
(135) 		145
(5) 		160
(20) 		166
(26) 		177
(37) 		190
(50) 		193
(53)

Possible tunings to be used on each page

You can remove some of these or add more that aren't listed here; this section is pretty much just brainstorming.

(Used https://x31eq.com/temper-pyscript/net.html, used WE instead of TE cause it kept defaulting to WE and I kept not remembering to switch it)

High-priority

60edo (narrow down edonoi & ZPIs)

  • 35edf
  • 139ed5
  • 301zpi (20.027c)
  • 95edt
  • 13-limit WE (20.013c) (155ed6 has octaves only 0.02 ¢ different)
  • 215ed12
  • 302zpi (19.962c)
  • 208ed11 (ideal for catnip temperament)
  • 303zpi (19.913c)

32edo

  • 13-limit WE (37.481c)
  • 11-limit WE (37.453c)
  • 90ed7 (optimal for dual-5) (133zpi's octave only differs by 0.4 ¢)
  • 51edt
  • 134zpi (37.176c)
  • 75ed5

33edo

  • 76ed5
  • 92ed7 (137zpi's octave differs by only 0.3 ¢)
  • 52ed13
  • 114ed11
  • 138zpi (36.394c) (122ed13's octave differs by only 0.1 ¢)
  • 13-limit WE (36.357c)
  • 93ed7 (optimised for dual-fifths)
  • 77ed5 (139zpi's octave differs by only 0.2 ¢)
  • 123ed13 / 1ed47/46 (identical within <0.1 ¢)
  • 115ed11

39edo

  • 171zpi (30.973c) (optimised for dual-fifths use)
  • 13-limit WE (30.757c) (octave of 135ed11 differs by only 0.2 ¢)
  • 101ed6 (octave of 172zpi differs by only 0.4 ¢)
  • 173zpi (30.672c) (octave of 62edt differs by only 0.2 ¢)
  • 110ed7 (octave of 145ed13 differs by only 0.1 ¢)
  • 91ed5

42edo

  • 108ed6 (octave is identical to 97ed5 within 0.1 ¢)
  • 189zpi (28.689c)
  • 150ed12
  • 145ed11

190zpi's octave is within 0.05 ¢ of pure-octaves 42edo

  • 118ed7
  • 13-limit WE (28.534c)
  • 151ed12 (octave is identical to 7-limit WE within 0.3 ¢)
  • 109ed6
  • 191zpi (28.444c)
  • 67edt

45edo

  • 209zpi (26.550)
  • 13-limit WE (26.695c)
  • 161ed12
  • 116ed6 (octave identical to 126ed7 within 0.1 ¢)
  • 7-limit WE (26.745c)
  • 207zpi (26.762)
  • 71edt (octave identical to 155ed11 within 0.3 ¢)

54edo

  • 139ed6 (octave is identical to 262zpi within 0.2 ¢)
  • 151ed7
  • 193ed12
  • 263zpi (22.243c)
  • 13-limit WE (22.198c) (octave is identical to 187ed11 within 0.1 ¢)
  • 264zpi (22.175c) (octave is identical to 194ed12 within 0.01 ¢)
  • 152ed7
  • 140ed6
  • 126ed5 (octave is identical to 86edt within 0.1 ¢)

59edo

  • 152ed6
  • 294zpi (20.399c)
  • 211ed12
  • 295zpi (20.342c)

pure octaves 59edo octave is identical to 137ed5 within 0.05 ¢

  • 13-limit WE (20.320c)
  • 7-limit WE (20.301c)
  • 166ed7
  • 212ed12
  • 296zpi (20.282c)
  • 153ed6

64edo

  • 179ed7 (octave is identical to 326zpi within 0.3 ¢)
  • 165ed6
  • 229ed12 (octave is identical to 221ed11 within 0.1 ¢)
  • 327zpi (18.767c)
  • 11-limit WE (18.755c)

pure octaves 64edo (octave is identical to 13-limit WE within 0.13 ¢

  • 328zpi (18.721c)
  • 180ed7
  • 230ed12
  • 149ed5
Medium priority

118edo (choose ZPIS)

Approximation of harmonics in 118edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.00 -0.26 +0.00 +0.13 -0.26 -2.72 +0.00 -0.52 +0.13 -2.17 -0.26 +3.54
Relative (%) +0.0 -2.6 +0.0 +1.2 -2.6 -26.8 +0.0 -5.1 +1.2 -21.3 -2.6 +34.8
Steps
(reduced) 		118
(0) 		187
(69) 		236
(0) 		274
(38) 		305
(69) 		331
(95) 		354
(0) 		374
(20) 		392
(38) 		408
(54) 		423
(69) 		437
(83)
  • 187edt
  • 69edf
  • 13-limit WE (10.171c)
  • Best nearby ZPI(s)

13edo

Approximation of harmonics in 13edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +36.5 +0.0 -17.1 +36.5 -45.7 +0.0 -19.3 -17.1 +2.5 +36.5 -9.8
Relative (%) +0.0 +39.5 +0.0 -18.5 +39.5 -49.6 +0.0 -20.9 -18.5 +2.7 +39.5 -10.6
Steps
(reduced) 		13
(0) 		21
(8) 		26
(0) 		30
(4) 		34
(8) 		36
(10) 		39
(0) 		41
(2) 		43
(4) 		45
(6) 		47
(8) 		48
(9)
  • Main: "13edo and optimal octave stretching"
  • 2.5.11.13 WE (92.483c)
  • 2.5.7.13 WE (92.804c)
  • 2.3 WE (91.405c) (good for opposite 7 mapping)
  • 38zpi (92.531c)

103edo (narrow down edonoi, choose ZPIS)

Approximation of harmonics in 103edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.00 -2.93 +0.00 -1.85 -2.93 -1.84 +0.00 +5.80 -1.85 -3.75 -2.93 -1.69
Relative (%) +0.0 -25.1 +0.0 -15.9 -25.1 -15.8 +0.0 +49.8 -15.9 -32.1 -25.1 -14.5
Steps
(reduced) 		103
(0) 		163
(60) 		206
(0) 		239
(33) 		266
(60) 		289
(83) 		309
(0) 		327
(18) 		342
(33) 		356
(47) 		369
(60) 		381
(72)
  • 163edt
  • 239ed5
  • 266ed6
  • 289ed7
  • 356ed11
  • 369ed12
  • 381ed13
  • 421ed17
  • 466ed23
  • 13-limit WE (11.658c)
  • Best nearby ZPI(s)

111edo (choose ZPIS)

Approximation of harmonics in 111edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.00 +0.75 +0.00 +2.88 +0.75 +4.15 +0.00 +1.50 +2.88 +0.03 +0.75 +2.72
Relative (%) +0.0 +6.9 +0.0 +26.6 +6.9 +38.4 +0.0 +13.8 +26.6 +0.3 +6.9 +25.1
Steps
(reduced) 		111
(0) 		176
(65) 		222
(0) 		258
(36) 		287
(65) 		312
(90) 		333
(0) 		352
(19) 		369
(36) 		384
(51) 		398
(65) 		411
(78)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)
Low priority

104edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

125edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

145edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

152edo

  • 241edt
  • 13-limit WE (7.894c)
  • Best nearby ZPI(s)

159edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

166edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

182edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

198edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

212edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

243edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

247edo

  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)
Optional

25edo

Approximation of harmonics in 25edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +18.0 +0.0 -2.3 +18.0 -8.8 +0.0 -11.9 -2.3 -23.3 +18.0 +23.5
Relative (%) +0.0 +37.6 +0.0 -4.8 +37.6 -18.4 +0.0 -24.8 -4.8 -48.6 +37.6 +48.9
Steps
(reduced) 		25
(0) 		40
(15) 		50
(0) 		58
(8) 		65
(15) 		70
(20) 		75
(0) 		79
(4) 		83
(8) 		86
(11) 		90
(15) 		93
(18)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

26edo

Approximation of harmonics in 26edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -9.6 +0.0 -17.1 -9.6 +0.4 +0.0 -19.3 -17.1 +2.5 -9.6 -9.8
Relative (%) +0.0 -20.9 +0.0 -37.0 -20.9 +0.9 +0.0 -41.8 -37.0 +5.5 -20.9 -21.1
Steps
(reduced) 		26
(0) 		41
(15) 		52
(0) 		60
(8) 		67
(15) 		73
(21) 		78
(0) 		82
(4) 		86
(8) 		90
(12) 		93
(15) 		96
(18)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

29edo

Approximation of harmonics in 29edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +1.5 +0.0 -13.9 +1.5 -17.1 +0.0 +3.0 -13.9 -13.4 +1.5 -12.9
Relative (%) +0.0 +3.6 +0.0 -33.6 +3.6 -41.3 +0.0 +7.2 -33.6 -32.4 +3.6 -31.3
Steps
(reduced) 		29
(0) 		46
(17) 		58
(0) 		67
(9) 		75
(17) 		81
(23) 		87
(0) 		92
(5) 		96
(9) 		100
(13) 		104
(17) 		107
(20)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

30edo

Approximation of harmonics in 30edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +18.0 +0.0 +13.7 +18.0 -8.8 +0.0 -3.9 +13.7 +8.7 +18.0 -0.5
Relative (%) +0.0 +45.1 +0.0 +34.2 +45.1 -22.1 +0.0 -9.8 +34.2 +21.7 +45.1 -1.3
Steps
(reduced) 		30
(0) 		48
(18) 		60
(0) 		70
(10) 		78
(18) 		84
(24) 		90
(0) 		95
(5) 		100
(10) 		104
(14) 		108
(18) 		111
(21)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

34edo

Approximation of harmonics in 34edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +3.9 +0.0 +1.9 +3.9 -15.9 +0.0 +7.9 +1.9 +13.4 +3.9 +6.5
Relative (%) +0.0 +11.1 +0.0 +5.4 +11.1 -45.0 +0.0 +22.3 +5.4 +37.9 +11.1 +18.5
Steps
(reduced) 		34
(0) 		54
(20) 		68
(0) 		79
(11) 		88
(20) 		95
(27) 		102
(0) 		108
(6) 		113
(11) 		118
(16) 		122
(20) 		126
(24)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

35edo

Approximation of harmonics in 35edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -16.2 +0.0 -9.2 -16.2 -8.8 +0.0 +1.8 -9.2 -2.7 -16.2 +16.6
Relative (%) +0.0 -47.4 +0.0 -26.7 -47.4 -25.7 +0.0 +5.3 -26.7 -8.0 -47.4 +48.5
Steps
(reduced) 		35
(0) 		55
(20) 		70
(0) 		81
(11) 		90
(20) 		98
(28) 		105
(0) 		111
(6) 		116
(11) 		121
(16) 		125
(20) 		130
(25)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

36edo

Approximation of harmonics in 36edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -2.0 +0.0 +13.7 -2.0 -2.2 +0.0 -3.9 +13.7 +15.3 -2.0 -7.2
Relative (%) +0.0 -5.9 +0.0 +41.1 -5.9 -6.5 +0.0 -11.7 +41.1 +46.0 -5.9 -21.6
Steps
(reduced) 		36
(0) 		57
(21) 		72
(0) 		84
(12) 		93
(21) 		101
(29) 		108
(0) 		114
(6) 		120
(12) 		125
(17) 		129
(21) 		133
(25)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

37edo

Approximation of harmonics in 37edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +11.6 +0.0 +2.9 +11.6 +4.1 +0.0 -9.3 +2.9 +0.0 +11.6 +2.7
Relative (%) +0.0 +35.6 +0.0 +8.9 +35.6 +12.8 +0.0 -28.7 +8.9 +0.1 +35.6 +8.4
Steps
(reduced) 		37
(0) 		59
(22) 		74
(0) 		86
(12) 		96
(22) 		104
(30) 		111
(0) 		117
(6) 		123
(12) 		128
(17) 		133
(22) 		137
(26)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

9edo

Approximation of harmonics in 9edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -35.3 +0.0 +13.7 -35.3 -35.5 +0.0 +62.8 +13.7 -18.0 -35.3 -40.5
Relative (%) +0.0 -26.5 +0.0 +10.3 -26.5 -26.6 +0.0 +47.1 +10.3 -13.5 -26.5 -30.4
Steps
(reduced) 		9
(0) 		14
(5) 		18
(0) 		21
(3) 		23
(5) 		25
(7) 		27
(0) 		29
(2) 		30
(3) 		31
(4) 		32
(5) 		33
(6)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

10edo

Approximation of harmonics in 10edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +18.0 +0.0 -26.3 +18.0 -8.8 +0.0 +36.1 -26.3 +48.7 +18.0 -0.5
Relative (%) +0.0 +15.0 +0.0 -21.9 +15.0 -7.4 +0.0 +30.1 -21.9 +40.6 +15.0 -0.4
Steps
(reduced) 		10
(0) 		16
(6) 		20
(0) 		23
(3) 		26
(6) 		28
(8) 		30
(0) 		32
(2) 		33
(3) 		35
(5) 		36
(6) 		37
(7)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

11edo

Approximation of harmonics in 11edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -47.4 +0.0 +50.0 -47.4 +13.0 +0.0 +14.3 +50.0 -5.9 -47.4 +32.2
Relative (%) +0.0 -43.5 +0.0 +45.9 -43.5 +11.9 +0.0 +13.1 +45.9 -5.4 -43.5 +29.5
Steps
(reduced) 		11
(0) 		17
(6) 		22
(0) 		26
(4) 		28
(6) 		31
(9) 		33
(0) 		35
(2) 		37
(4) 		38
(5) 		39
(6) 		41
(8)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

15edo

Approximation of harmonics in 15edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +18.0 +0.0 +13.7 +18.0 -8.8 +0.0 +36.1 +13.7 +8.7 +18.0 +39.5
Relative (%) +0.0 +22.6 +0.0 +17.1 +22.6 -11.0 +0.0 +45.1 +17.1 +10.9 +22.6 +49.3
Steps
(reduced) 		15
(0) 		24
(9) 		30
(0) 		35
(5) 		39
(9) 		42
(12) 		45
(0) 		48
(3) 		50
(5) 		52
(7) 		54
(9) 		56
(11)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

18edo

Approximation of harmonics in 18edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +31.4 +0.0 +13.7 +31.4 +31.2 +0.0 -3.9 +13.7 -18.0 +31.4 +26.1
Relative (%) +0.0 +47.1 +0.0 +20.5 +47.1 +46.8 +0.0 -5.9 +20.5 -27.0 +47.1 +39.2
Steps
(reduced) 		18
(0) 		29
(11) 		36
(0) 		42
(6) 		47
(11) 		51
(15) 		54
(0) 		57
(3) 		60
(6) 		62
(8) 		65
(11) 		67
(13)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

48edo

Approximation of harmonics in 48edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -2.0 +0.0 -11.3 -2.0 +6.2 +0.0 -3.9 -11.3 -1.3 -2.0 +9.5
Relative (%) +0.0 -7.8 +0.0 -45.3 -7.8 +24.7 +0.0 -15.6 -45.3 -5.3 -7.8 +37.9
Steps
(reduced) 		48
(0) 		76
(28) 		96
(0) 		111
(15) 		124
(28) 		135
(39) 		144
(0) 		152
(8) 		159
(15) 		166
(22) 		172
(28) 		178
(34)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

5edo

Approximation of harmonics in 5edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0 +18 +0 +94 +18 -9 +0 +36 +94 -71 +18 +119
Relative (%) +0.0 +7.5 +0.0 +39.0 +7.5 -3.7 +0.0 +15.0 +39.0 -29.7 +7.5 +49.8
Steps
(reduced) 		5
(0) 		8
(3) 		10
(0) 		12
(2) 		13
(3) 		14
(4) 		15
(0) 		16
(1) 		17
(2) 		17
(2) 		18
(3) 		19
(4)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

6edo

Approximation of harmonics in 6edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +98.0 +0.0 +13.7 +98.0 +31.2 +0.0 -3.9 +13.7 +48.7 +98.0 -40.5
Relative (%) +0.0 +49.0 +0.0 +6.8 +49.0 +15.6 +0.0 -2.0 +6.8 +24.3 +49.0 -20.3
Steps
(reduced) 		6
(0) 		10
(4) 		12
(0) 		14
(2) 		16
(4) 		17
(5) 		18
(0) 		19
(1) 		20
(2) 		21
(3) 		22
(4) 		22
(4)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

20edo

Approximation of harmonics in 20edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 +18.0 +0.0 -26.3 +18.0 -8.8 +0.0 -23.9 -26.3 -11.3 +18.0 -0.5
Relative (%) +0.0 +30.1 +0.0 -43.9 +30.1 -14.7 +0.0 -39.9 -43.9 -18.9 +30.1 -0.9
Steps
(reduced) 		20
(0) 		32
(12) 		40
(0) 		46
(6) 		52
(12) 		56
(16) 		60
(0) 		63
(3) 		66
(6) 		69
(9) 		72
(12) 		74
(14)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

24edo

Approximation of harmonics in 24edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -2.0 +0.0 +13.7 -2.0 -18.8 +0.0 -3.9 +13.7 -1.3 -2.0 +9.5
Relative (%) +0.0 -3.9 +0.0 +27.4 -3.9 -37.7 +0.0 -7.8 +27.4 -2.6 -3.9 +18.9
Steps
(reduced) 		24
(0) 		38
(14) 		48
(0) 		56
(8) 		62
(14) 		67
(19) 		72
(0) 		76
(4) 		80
(8) 		83
(11) 		86
(14) 		89
(17)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)

28edo

Approximation of harmonics in 28edo
Harmonic 2 3 4 5 6 7 8 9 10 11 12 13
Error Absolute (¢) +0.0 -16.2 +0.0 -0.6 -16.2 +16.9 +0.0 +10.4 -0.6 +5.8 -16.2 +16.6
Relative (%) +0.0 -37.9 +0.0 -1.4 -37.9 +39.4 +0.0 +24.2 -1.4 +13.6 -37.9 +38.8
Steps
(reduced) 		28
(0) 		44
(16) 		56
(0) 		65
(9) 		72
(16) 		79
(23) 		84
(0) 		89
(5) 		93
(9) 		97
(13) 		100
(16) 		104
(20)
  • Nearby edt, ed6, ed12 and/or edf
  • Nearby ed5, ed10, ed7 and/or ed11 (optional)
  • 1-2 WE tunings
  • Best nearby ZPI(s)
Retrieved from "https://en.xen.wiki/index.php?title=User:BudjarnLambeth/Sandbox2&oldid=208767"