Plücker coordinates
| This is an expert page. It is written to allow experienced readers to learn more about the advanced elements of the topic. The corresponding beginner page for this topic is Wedgie. |
In exterior algebra applied to regular temperament theory, Plücker coordinates (also known as the wedgie) are a way to assign coordinates to abstract temperaments, by viewing them as elements of some projective space.
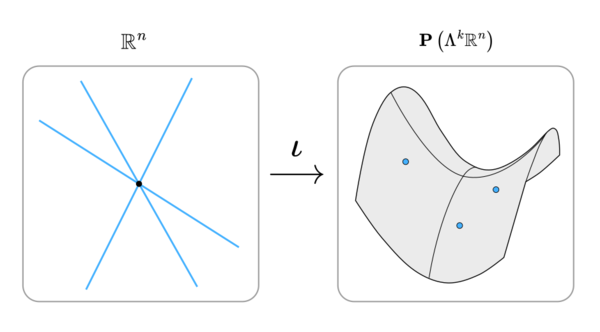
The usual way to write down an abstract temperament is via its mapping matrix, but Plücker coordinates give us a unique description that is useful for some calculations. The definition here is given in terms of temperament matrices, but by duality, we can also embed interval spaces in the same way. More specifically, the interval subspace spanned by the commas of some temperament can also be used to give unique coordinates to that temperament. These two representations are related via the Hodge dual.
Definition
A temperament can be viewed as a point in what is called a Grassmannian variety, written as [math]\displaystyle{ \mathrm{Gr} (k, n) }[/math]. This variety contains all possible k-dimensional subspaces of [math]\displaystyle{ \mathbb{R}^n }[/math]. In musical terms, k represents the rank of the temperament (how many independent generators it has), and n is the number of primes we're considering in our just intonation subgroup.
Let [math]\displaystyle{ M }[/math] be an element of [math]\displaystyle{ \mathrm{Gr} (k, n) }[/math], spanned by basis vectors [math]\displaystyle{ m_1, \ldots, m_k }[/math]. These basis vectors are the rows of the temperament mapping matrix.
The Plücker map takes a temperament and embeds it into a projective space by taking the wedge product of the basis vectors:
- [math]\displaystyle{ \begin{align} \iota: \mathrm{Gr} (k, n) & \to \mathbf{P}\left(\Lambda^{k} \, \mathbb{R}^n \right) \\ \operatorname {span} (m_1, \ldots, m_k) & \mapsto \left[ m_1 \wedge \ldots \wedge m_k \right] \, . \end{align} }[/math]
Here, [math]\displaystyle{ \Lambda^{k} \, \mathbb{R}^n }[/math] is the k-th exterior power (the subspace containing all k-vectors). This construction is independent of the basis we choose. While the original space of temperaments has dimension [math]\displaystyle{ k(n-k) }[/math], the space of Plücker coordinates is typically larger, with dimension [math]\displaystyle{ \binom{n}{k} - 1 }[/math].
Examples
The space of lines through the origin is exactly projective space, so [math]\displaystyle{ \mathrm{Gr} (1, n) \cong \mathbf{P} (\mathbb{R}^n) }[/math]. In 3 dimensions, a plane through the origin is completely defined by its normal, so we get that [math]\displaystyle{ \mathrm{Gr} (2, 3) \cong \mathrm{Gr} (1, 3) \cong \mathbf{P} (\mathbb{R}^3) }[/math], the projective plane.
The simplest non-trivial case is [math]\displaystyle{ \mathrm{Gr} (2, 4) }[/math]. An element [math]\displaystyle{ M }[/math] spanned by two lines [math]\displaystyle{ x, y }[/math], can be represented as the matrix
- [math]\displaystyle{ \begin{equation} \begin{bmatrix} x_{1} & x_{2} & x_{3} & x_{4} \\ y_{1} & y_{2} & y_{3} & y_{4} \end{bmatrix} \, . \end{equation} }[/math]
These are not 'proper' coordinates, as doing row operations on this matrix preserves the row-span.
The projective coordinates can be calculated by taking the determinants of all [math]\displaystyle{ 2 \times 2 }[/math] sub-matrices
- [math]\displaystyle{ p_{ij} = \begin{vmatrix} x_i & x_j \\ y_i & y_j \end{vmatrix} \, , }[/math]
which finally gives us
- [math]\displaystyle{ \begin{equation} \iota (M) = \left[ x \wedge y \right] = \left[ p_{12} : p_{13} : p_{14} : p_{23} : p_{24} : p_{34} \right] \, . \end{equation} }[/math]
Note the use of colons to signify that these coordinates are homogeneous.
Plücker relations
The coordinates must satisfy some algebraic relations called Plücker relations. Generally, the projective space is much 'larger' than the Grassmannian, and the image in the projective space is some quadric surface.
For the example above on [math]\displaystyle{ \mathrm{Gr} (2, 4) }[/math], the Plücker relation is
- [math]\displaystyle{ p_{12} p_{34} - p_{13} p_{24} + p_{14} p_{23} = 0 \, . }[/math]
Note that in this case, there is only one such relation, but in higher dimensions there will be many.
Rational points
A rational point [math]\displaystyle{ P }[/math] on [math]\displaystyle{ \mathrm{Gr}(k, n) }[/math] is a k-dimensional subspace such that [math]\displaystyle{ \mathcal{L} = P \cap \mathbb{Z}^n }[/math] is a rank k sublattice of [math]\displaystyle{ \mathbb{Z}^n }[/math]. Abstract temperaments correspond exactly to these rational points, although most have no practical musical use.
The same relations as above can be derived, where we represent P as integer matrix [math]\displaystyle{ M \in \mathbb{Z} ^ {k \times n} }[/math], whose rows span [math]\displaystyle{ \mathcal{L} }[/math]. The projective coordinates similarly have integer entries. Because the Plücker coordinates are homogeneous, we can always put them in a canonical form by dividing all entries by their greatest common divisor (GCD) and ensuring the first element is non-negative.
An advantage of studying rational points is that we do not have to worry about torsion. The quotient group [math]\displaystyle{ \mathbb{Z}^n / \mathcal{L} }[/math] is a finitely generated abelian group. When the Plücker coordinates are normalized (GCD = 1), we ensure that [math]\displaystyle{ \mathbb{Z}^n / \mathcal{L} \cong \mathbb{Z}^{n-k}, }[/math] which is torsion-free.
Height
A height function is a way to measure the 'arithmetic complexity' of a rational point. For example, the rational numbers [math]\displaystyle{ \frac{3}{2} }[/math] and [math]\displaystyle{ \frac{3001}{2001} }[/math] are close to eachother, but intuitively the second is much more complicated.
We can define the height of a rational point simply as the Euclidean norm on its Plücker coordinates [math]\displaystyle{ X = \iota (P) }[/math].
- [math]\displaystyle{ H(P) = \left\| X \right\| = \left\| m_1 \wedge \ldots \wedge m_n \right\| \\ }[/math]
In terms of the lattice defined by P, this definition is equivalent to the volume of the fundamental domain, also known as the lattice determinant. It is easy to show that this does not depend on the basis we choose.
The height can be easily computed using the Gram matrix:
- [math]\displaystyle{ \begin{align} \mathrm{G}_{ij} &= \left\langle m_i, m_j \right\rangle \\ \sqrt{\det(\mathrm{G})} &= \left\| m_1 \wedge \ldots \wedge m_n \right\| = \left\| X \right\| \, . \end{align} }[/math]
In regular temperament theory, this height is usually known as simply the complexity.
Projective distance
Given a temperament, we want to have some notion of distance, so that we can measure how well the temperament approximates JI. Since we are talking about linear subspaces (which all intersect at the origin), the only thing that is sensible to measure is the angle between them.
In Euclidean space, one usually takes advantage of the dot product to measure angles. Given vectors [math]\displaystyle{ a, b \in \mathbb{R^n} }[/math], we famously have
- [math]\displaystyle{ \frac{a \cdot b}{\left\| a \right\| \left\| b \right\| } = \cos (\theta) \, . }[/math]
In projective space, there is an analogous formula, using the wedge product instead. Given some real point [math]\displaystyle{ j \in \mathbb{R^n} }[/math] with homogeneous coordinates [math]\displaystyle{ y }[/math], and a linear subspace [math]\displaystyle{ P \in \mathrm{Gr} (k, n) }[/math] with Plücker coordinates [math]\displaystyle{ X }[/math], we define the projective distance as
- [math]\displaystyle{ d(P, j) = \frac{ \left\| X \wedge y \right\| }{\left\| X \right\| \left\| y \right\| } = \sin (\theta) \, . }[/math]
Where we can take [math]\displaystyle{ j }[/math] to be the usual n-limit vector of log primes, so that [math]\displaystyle{ y = \left[ 1 : \log_2 (3) : \ldots : \log_2 (p_n) \right] }[/math]. Unlike the dot product formula, this works for subspaces of any dimension.
Since for any decent temperament this angle will be extremely small, we can take [math]\displaystyle{ \sin (\theta) \approx \theta }[/math].
See also
- Wedgie supplement - Supplementary page going over additional information on wedgies
- Exterior algebra - exterior product, which produces wedgies
- Interior product - interior product, dual of the exterior product
- Hodge dual - acts on wedgies
