Combination product set
A combination product set (CPS) is a scale generated by the following means:
- A set S of n positive real numbers is the starting point.
- All the combinations of k elements of the set are obtained, and their products taken.
- These are combined into a set, and then all of the elements of that set are divided by one of them (which one is arbitrary; if a canonical choice is required, the smallest element could be used).
- The resulting elements are octave-reduced and sorted in ascending order, resulting in an octave period of a periodic scale (the usual sort of scale, in other words) which we may call CPS(S, k).
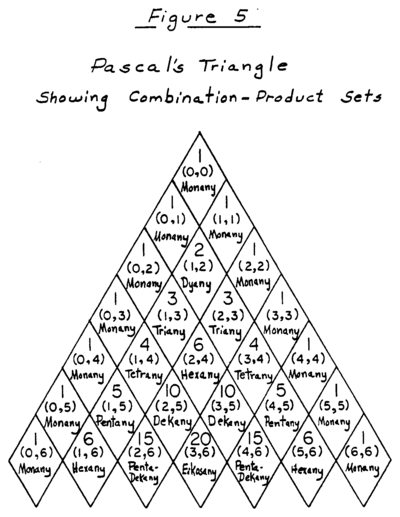
This is sometimes called a k)n CPS, where the n denotes the size of the set S. There are special names for special cases: a 2)4 CPS is called a hexany; both 2)5 and 3)5 CPS are called dekanies; both 2)6 and 4)6 CPS are called pentadekanies, a 3)6 CPS is called an eikosany, etc. These are normally considered in connection with just intonation, so that the starting set is a set of positive rational numbers, but nothing prevents consideration of the more general case.
The idea can be further generalized so that the thing we start from is not a set but a multiset. A multiset is like a set, but the elements have multiplicities; there can be two, three or any number of a given kind of element. Submultisets of a multiset are also multisets, and the product over a multiset takes account of multiplicity. Hence the 2)4 hexany resulting from the multiset [1,1,3,5] first generates the two-element submultisets, which are [1, 1], [1, 3], [1, 5], [3, 5], and we obtain products 1, 3, 5, and 15. Reducing to an octave gives 5/4, 3/2, 15/8, 2 which can be transposed to 5/4, 4/3, 5/3, 2. In spite of being called a hexany it has only four notes.
CPS are closely related to Euler genera, since if we combine 0)n, 1)n, 2)n ... n)n before reducing to an octave, and then reduce, we get an Euler genus.
CPS were invented by Erv Wilson.